Моделирование параллельной реализации марковских моделей в многопроцессорных вычислительных системах
Автор: Мищук Ю.К., Фельдман Л.П.
Источник: Материіали I всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених – 19-21 травня 2010р., Донецьк, ДонНТУ. – 2010. – с. 238-240
Общая постановка проблемы
В связи с необходимостью увеличения вычисляемых мощностей во многих сферах жизнедеятельности человека, активно разрабатываются алгоритмы улучшения работы вычислительных систем – систем обработки данных, настроенных на решение задач, конкретной области применения. Вычислительная система включает в себя технические средства и программное обеспечение, ориентированные на решение определенной совокупности задач. Основополагающими в теории вычислительных систем являются модели и аппарат теории марковских процессов.
Постановка задач исследования
Понятие архитектуры высокопроизводительной системы является достаточно широким, поскольку под архитектурой можно понимать и способ параллельной обработки данных, используемый в системе, и организацию памяти, и топологию связи между процессорами, и способ исполнения системой арифметических операций. Рассматривается кластерная архитектура многопроцессорных вычислительных систем [1]. Учитывая трудоёмкость и большие объемы данных, марковские модели не использовались в больших системах, поэтому задача является актуальной [7]. В данной работе необходимо проанализировать эффективность распараллеливания метода и выяснить, насколько ускорилось моделирование многопроцессорной системы.
Решение задачи и результаты исследований
Для решения поставленной задачи был проведен обзор современных вычислительных систем и обзор методов анализа вычислительных систем. Так же был произведен анализ построения марковских моделей и его распараллеливание.
Определяющими при распараллеливании алгоритма являются:
- количество узлов вычислительного кластера;
- количество процессов на кластере;
- способ размещения данных;
- методы коммутации.
Одной из систем классификации кластерных систем является классификация по совместному использованию одних и тех же дисков отдельными узлами: кластеры с совместным и раздельным использованием дискового пространства [2].
В работе рассмотрена модель кластера с совместным использованием дискового пространства. Упрощенная модель кластера с совместным использованием дискового пространства приведена на рис. 1.
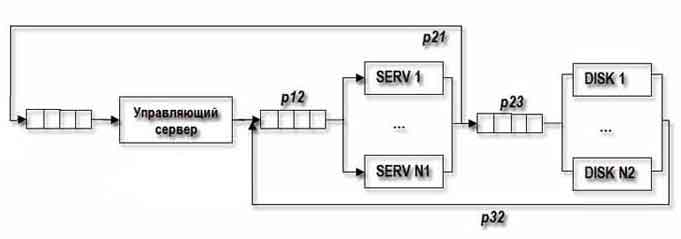
Рисунок 1 — Структурная схема кластера с совместным использованием дискового пространства.
В вычислительной системе, приведенной на рисунке 1, М задач или пользователей, N1 однотипных кластеров-серверов и N2 дисков, на которых хранятся данные. Каждый из М пользователей посылает с вероятностью P 12, запрос к одному из N1 серверов, которые, в свою очередь, обрабатывая этот запрос, обращаются к одному из N2 дисков с вероятностью P 23. Вероятность завершения обслуживания задачи одним из N2 дисков и поступление на i-й сервер тогда будет – P 32 [i = 1..N1]. А P 10 – это вероятность завершения обслуживания задачи и q0 – вероятность появления новой задачи.
Функционирование рассматриваемой системы можно представить замкнутой стохастической сетью [4], содержащей три системы массового обслуживания (СМО), в которой циркулирует М заявок. Граф передач этой сети изображен на рис.2, на котором введены следующие обозначения:
- - S1 — СМО, соответствующая клиентам (т.е. заявкам);
- - S2 — СМО, соответствующая серверам;
- - S3 — СМО, соответствующая дисковым пространствам.

Рисунок 2 — Граф передач.
Алгоритм, примененный в параллельной реализации марковских моделей [5,6], состоит из двух частей: вычислений матрицы переходных вероятностей и вектора стационарных вероятностей.
1. Расчет стационарных вероятностей реализован с использованием итерационного алгоритма, в котором в качестве базового используется алгоритм умноження матрицы на вектор.
2. Вычисление элемента матрицы переходных вероятностей не зависит от соседних элементов, следовательно, в основе параллельной реализации этой части параллельного алгоритма можно использовать принцип распараллеливания по данным. Суть заключается в том, в задаче выделены отдельные независимые части – ветви программы, которые при наличии нескольких обрабатывающих устройств могут выполняться параллельно и независимо друг от друга. В качестве базовой подзадачи в алгоритме взят расчет строки матрицы переходных вероятностей, которая характеризуется одинаковой вычислительной трудоемкостью.
Выводы
В работе дано решение актуальной научной задачи, связанной с развитием методов и исследования параллельного алгоритма построения марковских моделей многопроцессорных вычислительных систем в корпоративных компьютерных сетях для анализа качества их функционирования, прогнозирования свойств и моделирования.
Параллельный алгоритм марковских моделей многопроцессорных вычислительных систем позволяют моделировать любые многопроцессорные структуры. Эти алгоритмы можно использовать при анализе, синтезе и модернизации вычислительных структур. Они быстро вычисляются в масштабе реального времени и поэтому могут использоваться для реконфигурации вычислительных систем в режиме реального времени.
Использование параллельного алгоритма позволяет повысить эффективность исследуемой вычислительной структуры.
Предполагается исследование эффективности параллельного алгоритма построения марковской модели на параллельных структурах различной топологии с целью выяснения оптимальности параллельной вычислительной структуры.
Список литературы
1. Основы вычислительных систем. Курс лекций. Модели и методы. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://256bit.ru/education/infor2/lecture7-2.htm
2. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя. Киев: ДиаСофт, 1998.
3. Фельдман Л.П., Михайлова Т.В. Вероятностные модели анализа оценки эффективности кластерных систем // Материалы II Международного научно-практического семинара «Высокопроизводительные параллельные вычисления на кластерных системах» — Нижний. Новгород: Изд-во НГУ, 2002. – С. 301-307
4. Основы теории вычислительных систем / С.А.Майоров, Г.И.Новиков, Т.И.Алиев и др. М.: Высшая школа, 1978.
5. Михайлова Т.В. Параллельный алгоритм построения дискретной модели Маркова // Искусственный интеллект. Интеллектуаьные и многопроцесорные системы. Материалы Международной научно-технической конференции, 25-30 сентября 2006г., Таганрог-Донецк-Минск, 2006.
Фельдман Л.П., Михайлова Т.В. Использование аналитических методов для оценки эффективности многопроцессорных вычислительных систем. //Электронное моделирование, Т.29, №2, 2007.- С.17-27
7. Фельдман Л.П., Михайлова Т.В. Дискретная модель Маркова однородного кластера // Искусственный интеллект.- Донецк: ІПШІ МОН і НАН України “Наука і освіта”, №3, 2006. - С. 79-91.