ПРЕОБРАЗОВАНИЕ СЛОЖНЫХ ЭКВИВАЛЕНТНЫХ СХЕМ ЗАМЕЩЕНИЯ ТУРБОГЕНЕРАТОРОВ К ВИДУ, УДОБНОМУ ДЛЯ МОДЕЛИРОВАНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ

Авторы: А.М. Ларин, Гуедиди Фаузи Бен Килани

Источник: Вестник Восточноукраинского национального университета  – 2007. – №11(117), ч. 1. – стр. 108 – 115.

Введение. В настоящее время для математического описания синхронных машин (СМ) наибольшего распространения получила система полных дифференциальных или операторных уравнений электромагнитного состояния (уравнения Парка-Горева). Эти уравнения позволяют описывать переходные процессы машин переменного тока с учетом влияния неограниченного числа контуров в роторе. Моделирование переходных процессов предполагает, в этом случае, известность определенной совокупности активных и индуктивных сопротивлений, отражающих связь между токами и потокосцеплениями в магнитосвязанных контурах машины. Такая исходная информация представляется в форме схем замещения физически обоснованной структуры, имеющих различную степень детализации.

Дифференциальные уравнения, записанные относительно изменений потокосцеплений в осях ротора d, q не зависят от структуры принятых для моделирования эквивалентных схем замещения. Токи, используемые в них, определяются из соотношений, связывающих потокосцепления с токами через собственные и взаимные индуктивности соответствующих ветвей схемы замещения.

Значения собственных и взаимных сопротивлений, используемых для отражения связи между потокосцеплениями и токами в магнитосвязанных контурах, зависят от структуры принятой в качестве математической модели эквивалентной схемы замещения. Следовательно, для каждой структуры схемы замещения при использовании ПЭВМ требуется составление соответствующей программы расчета. Поэтому актуальной является задача разработки метода преобразования схем замещения различных структур к одному наиболее простому виду, удобному для моделирования динамических режимов.

Целью настоящей работы является разработка метода преобразования сложных эквивалентных схем различных структур от одного вида к другому. Это позволит составить универсальную программу расчета на ЭВМ для исследования различных видов переходных процессов.

Анализ существующих схем. Наиболее широко используются схемы замещения, в которых предполагается, что цепи обмотки статора, возбуждения и демпферных контуров имеют магнитную связь только через основное магнитное поле взаимной реактивностью . В таких схемах замещения Т – образного типа (рис. 1) обмотка возбуждения генератора (ОВГ) может представляться одним контуром или самостоятельной многоконтурной цепью [1].

В последнее время появились работы [2,3], посвященные построению и использованию схем замещения уточненной структуры (рис. 2). Они более достоверны с физической точки зрения, поскольку в них учитывается различие взаимной индуктивной магнитной связи между обмотками статора, возбуждения и эквивалентными контурами демпферной системы.

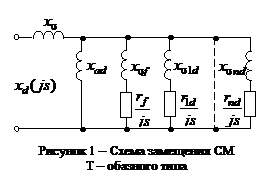При использовании для моделирования схем замещения с различной магнитной связью между контурами, как правило, демпферную систему представляют упрощенно в виде одного эквивалентного контура.

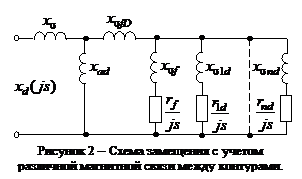Сотрудниками Сибирского НИИ энергетики предложены и получены более сложные структуры эквивалентных схем замещения турбогенераторов, также учитывающих различную взаимоиндуктивную связь между контурами, расположенными на роторе. Основной отличительной особенностью таких схем замещения является представление демпферной системы машины по продольной и поперечной осям ротора в виде основного демпферного контура, охватывающего магнитный поток взаимоиндукции между статором и ротором, и ряда локальных контуров, охватывающих магнитные потоки рассеяния и обмотки возбуждения. В этом случае обмотка возбуждения генератора, его демпферная система и взаимная индуктивность между ними характеризуются сложными зависимостями от скольжения высокого порядка (рис. 3).

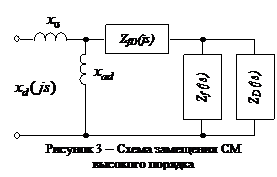В приведенных схемах замещения не рассматриваются токи в каждом клине и в отдельных элементах массива активной и торцевой зон ротора СМ. В [4] предложены сложные схемы замещения турбогенераторов применительно к расчету установившихся анормальных режимов, связанных с большими скольжениями (несимметричная нагрузка, несимметричные короткие замыкания, неполнофазные режимы), которая учитывает наличие на роторе реальных физических контуров.

При использовании схем замещения, приведенных на рис.1 и 2, процедура нахождения токов в контурах статора и ротора при исследовании переходных процессов не вызывает трудностей. Анализ с помощью сложных эквивалентных схем высокого порядка (рис. 3) и предложенных в [4] вызывает принципиальные сложности в определении этих токов. При расчете переходных процессов, например в операторной форме, это приводит к сложным операторным выкладкам, не всегда дающим возможность при практических расчетах выполнить переход во временную область. Поэтому значительно удобнее иметь схемы замещения с постоянными параметрами вида, показанного на рис 1 и 2.

Для общего анализа переходных процессов с точки зрения выявления экстремальных значений параметров режима дифференциальные уравнения неудобны. Для этих целей разрабатываются модели ЭМ, основанные на аналитическом описании переходных процессов. В [5] предлагается использование частотного метода рассмотрения динамических режимов, который позволяет решать ряд задач на основе получения общего решения в аналитическом виде.

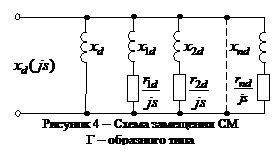При частотном методе расчета переходных процессов более эффективным является аналитическое описание частотных характеристик с помощью Г-образных схем замещения с вынесенной на зажимы источника ветвью намагничивания (рис.4). Следует также отметить, что указанная форма информации о совокупности электромагнитных параметров СМ является наиболее удобной с точки зрения хранения ее в памяти ЭВМ и последующего определения на ее основе переходных функций.

Общий путь преобразования эквивалентных схем замещения от одной структуры к другой заключается в синтезе параметров схемы замещения необходимой структуры по комплексам частотной характеристики входного сопротивления  или проводимости  схемы исходной структуры.

В [6] разработан способ определения параметров n параллельных цепочек схемы замещения по n комплексам проводимости . На его основе может быть осуществлен переход от схемы замещения любой структуры к схеме замещения, представленной на рис.4. В этом случае при числе контуров в схеме замещения Г – образного типа, равном числу контуров в исходной схеме, отличие частотных характеристик проводимостей или сопротивлений не превышает заданной точности в процедуре итерационного расчета. Параллельные цепочки в схемах, показанных на рис.4, не представляют реальные обмотки или демпферные контура на роторе, а только характеризуют их взаимное влияние, поскольку ток в каждой из них представляет собой одну из составляющих переходного тока статора, изменяющегося с одной постоянной времени. Из этого следует, что при использовании схем замещения с вынесенной на зажимы источника ветвью намагничивания, параметры которой рассчитываются только на основе адекватности частотных характеристик входных сопротивлений , или проводимостей  со стороны обмотки статора, решить задачу определения токов в обмотках, расположенных на роторе, не представляется возможным.

                Поскольку ток в каждой из n магнитосвязанных обмоток изменяется с n постоянными времени, то в Г – образных эквивалентных схемах замещения, каждый из реальных контуров на роторе должен быть представлен самостоятельной многоконтурной цепью. Это приведет к увеличению контуров схеме замещения в n раз. Однако, в большинстве задач исследования переходных процессов ограничиваются точным определением только тока в обмотке возбуждения. Токи в массивных конструктивных элементах ротора учитываются эквивалентно. В этом случае схема замещения, отражающая влияние n контуров на роторе, будет иметь 2n параллельных цепочек. Из них n ветвей будут характеризовать ОВГ, а остальные эквивалентно представлять демпферную систему (рис. 5).

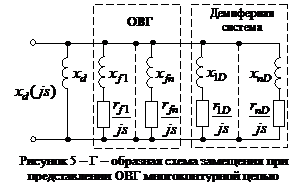Кроме соблюдения адекватности частотных характеристик  исходной и преобразованной схем замещения синтез последней необходимо осуществлять при равенстве комплексного коэффициента распределения тока статора в ветви ОВГ () для всех значений скольжений ротора. 

               

Основные математические соотношения. Рассмотрим алгоритм преобразования схем замещения к Г – образному виду при представлении ОВГ многоконтурной цепью (рис. 5).

Определив частотную характеристику комплексного коэффициента в исходной схеме замещения, рассчитываем частотную характеристику проводимости n параллельных контуров, отражающих влияние обмотки возбуждения в преобразованной схеме , по соотношению

.                                     (1)

Тогда частотная характеристика проводимости контуров, отражающих влияние демпферной системы синхронной машины , находится следующим образом:

.                   (2)

                Применив к левым частям выражений (1) и (2) методику, изложенную в [6], определяем соответственно параметры n контуров, учитывающих влияние ОВГ, и столько же - демпферной системы. Очевидно, что активные и индуктивные сопротивления некоторых из них могут иметь отрицательные величины.

                Для схемы замещения, представленной на рис.1, зависимость коэффициента участия  от частоты определяется в соответствии со следующим соотношением:

,                                                      (3)

                где  - зависимость от частоты проводимости ОВГ; - частотная характеристика проводимости, измеренная относительно зажимов ветви сопротивления взаимоиндукции ,

.                                                (4)

                Для схем замещения, приведенных на рис. 2 и 3, имеем

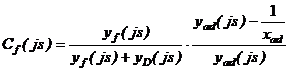.                                               (5)

                В (5) проводимость  в соответствии со структурой схем замещения рассчитывается в соответствии с соотношением:

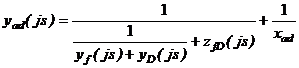.                                           (6)

                Оценка эффективности метода преобразования. Проверка достоверности предложенной в работе методики преобразования сложных схем замещения на основе адекватности распределения тока в обмотке возбуждения проводилась для синхронных генераторов различных конструкций и мощностей. Типы исследуемых генераторов и параметры их исходных схем замещения приведены в таблице 1. Рассматривался генератор типа СГ-18.75, не имеющий демпферной системы. Турбогенератор типа ТГВ-300 представлялся одним эквивалентным демпферным контуром по каждой оси ротора. Модельный синхронный генератор типа МТ-30 характеризовался тремя контурами по каждой из осей симметрии. Для турбогенератора типа ТВВ-160-2 методика проверялась для схемы замещения уточненной структуры (рис. 2) только для продольной оси ротора. Схемы замещения по поперечной оси преобразовывались во всех случаях к виду, представленному на рис. 4.

                Параметры полученных после преобразования Г-образных эквивалентных схем замещения при представлении обмотки возбуждения многоконтурной цепью приведены в таблице 2.

Таблица 1- Параметры исходных схем замещения синхронных генераторов

Тип синхронного генератора	Параметры роторных контуров
СГ-18.75 0,041; 0,779; 0,779	0,0009 -	0,0014 -	- -	- -	- -	- -
ТГВ-300 0,170; 2,025; 2,025	0,1390 0,0253	0,0013 0,0048	0,0310 -	0,0023 -	- -	- -
МТ-30 0,053; 1,400; 1,343	0,1385 1,2160	0,0031 0,0212	0,2379 0,2564	0,0211 0,0212	0,0981 0,3986	0,0782 0,1353
ТВВ-160-2 0,188; 2,012; 0,011	0,1450	0,0015	0,1000	0,0218	-	-

Частотные характеристики ,  и , соответствующие исходным и преобразованным схемам замещения, совпали между собою.

Таблица 2 - Параметры Г - образных схем замещения СГ по продольной оси  ротора при выделении контура ОВГ

Тип синхронного Генератора	Параметры роторных контуров
СГ-18.75	0,14800 0,00097	- -	- -	-2,95500 -0,01900	- -	- -
ТГВ-300	0,34600 0,00132	-0,50800 -0,01360	- -	1,33100 0,00507	0,33400 0,00894	- -
МТ-30	0,19200 0,00313	-1,19400 -0,09230	-0,94400 -0,57060	7,95600 0,12960	0,42000 0,03247	0,26900 0,16250
ТВВ-160-2	0,39400 0,00153	-0,53500 -0,06761	- -	-9,56700 -0,03730	0,34500 0,04360	- -

Достоверность преобразованных схем замещения для всех исследуемых машин оценивалась также путем расчета электромагнитных переходных процессов при внезапном коротком замыкании на выводах СМ и электромеханических, вызванных выпадением из синхронизма и переходом к установившемуся асинхронному режиму после потери возбуждения. Изменения во времени токов в обмотках статора и ротора для исходных и преобразованных схем также совпали.

Вывод. Предложенный в работе метод преобразования эквивалентных схем замещения, основанный на адекватности частотных характеристик проводимости со стороны обмотки статора и комплексных коэффициентов распределения тока статора в ветви обмотки возбуждения позволяет упрощать сложные схемы замещения высокого порядка к простому виду, удобному для моделирования переходных процессов на основе аналитического описания электромагнитных переходных процессов.

Список литературы

1. Сидельников А.В. Синтез схемы замещения синхронной машины при представлении обмотки возбуждения многоконтурной цепью // Электротехника. – 1983. - №7. – С. 25-28.

2. Сивокобыленко В.Ф., Лебедев В.К., Гармаш В.С. Идентификация параметров синхронных и асинхронных машин по данным измерений на неподвижной машине // Изв. АН СССР. Энергетика и транспорт. – 1989. - №4. – С.49-57.

3. Escarela-Perez R., Campero-Littlewood E., Niewierowicz T., Hernandez-Anaya. Unique Determination of One-Damper D-Axis Circuits of Synchronous Machines Using Finite-Element Simulations // IEEE Transactions on Energy Conversion.- 2005. - Vol.-16, No 2. – P. 137 – 142.

4. Шапиро А.С. Схема замещения турбогенератора при больших скольжениях с учетом клиньев и торцевого эффекта // Турбо- и гидрогенераторы большой мощности и перспективы их развития. – Л.: Наука, 1969. – С. 153-167.

5. Larin A. Lamary A. Computer simulation of the transient in AC machines at short-circuits and connections to a network on the basis of the experimental frequency-response characteristics // 9th International Symposium on Short-circuit currents in power systems, SCC'2000, Cracow, October 11-13, 2000. - P. 39-45.

6. Рогозин Г.Г., Ларин А.М. Расчет параметров эквивалентных роторных контуров синхронных машин по их экспериментальным частотным характеристикам // Электричество. - 1974. - № 6. - С.10-13.