Источник: Автоматизация технологических объектов и процессов. Поиск молодых / Материалы ХІ Международной  научно-технической конференции "Автоматизация технологических объектов и процессов. Поиск молодых", будет опубликована 17 - 20 мая 2011 года, ДонНТУ, Донецк

Охрана окружающей среды от загрязнений становится одной из наиболее актуальных проблем науки и техники. Для проведения эффективных природоохранных мероприятий необходим качественный контроль за состоянием выбросов в окружающую среду от всех источников загрязнения. Сложность в оперативном и точном определении количества выбросов в атмосферу состоит в учете влияющих факторов, таких как диффузия и перенос примесей, устойчивость атмосферы (температура, давление, скорость, направление и размах вихрей ветра, интенсивность турбулентности). Массовая доля выбросов в мире, приходящаяся на транспорт, с каждым годом возрастает [1]. Поэтому в качестве источника загрязнения в приведенных исследованиях выбран автотранспорт.

Цель работы состоит в разработке математической модели для определения количества выбрасываемых автомобилем вредных веществ в атмосферу.

В качестве источника выбросов рассматривается легковой автомобиль, находящийся в движении. Для описания процесса рассеивания газообразных продуктов выброса используется модель нестационарного переноса [1]. Так как наибольшую долю среди токсичных веществ занимает оксид углерода, то его концентрация и будет определяться. При составлении математической модели были использованы следующие основные уравнения: уравнения газовой диффузии, уравнение переноса и распространения примесей и уравнение движения. Считая автомобиль точечным источником выброса в определенные моменты времени, поместим трехмерную декартовую систему координат непосредственно в источник выбросов. При это ось OZ – вдоль дороги, ось OX – определяет ширину дороги и ось OY – перпендикулярно осям OZ и OX соответственно.

Рассмотрим поведение выхлопа в плоскости XZ, без учета сложных погодных  условий (рисунок 1). Также обозначим на рисунке 1 все влияющие величины, которые будут учтены в математической модели.

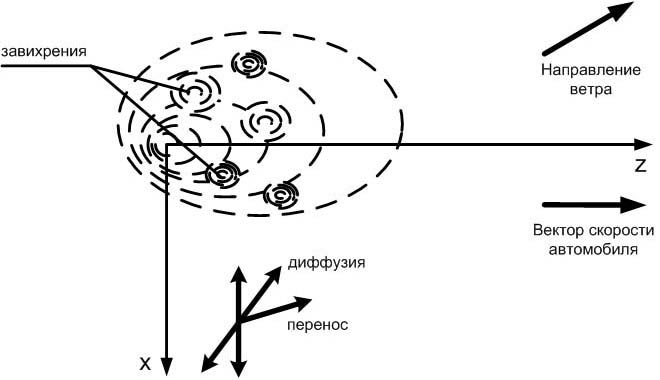
Рисунок 1 – Поведения выхлопа в атмосфере

Концентрация оксида углерода в районе выброса будет описываться следующим уравнением:

Cco(x,y,z,t,Va,Vb) = Cфонаглоб(x,y,z,t) + Cфоналокальн(x,y,z,t) + Савто(x,y,z,t,Va,Vb), где

Cco(x,y,z,t,Va,Vb) - суммарная концентрация  оксида углерода в районе выброса;

Cфонаглоб(x,y,z,t) - глобальная фоновая концентрация;

Cфоналокальн(x,y,z,t) - локальная фоновая концентрация, которая характерна данной местности;

Савто(x,y,z,t,Va,Vb) - концентрация, вносимая отработанными газами автотранспорта.

Глобальная и фоновая концентрации имеют среднестатистическое значение для определенной местности, участка трассы и погодных условий и определяется экспериментально либо на основе статистических данных.

Концентрация, вносимая отработанными газами автомобиля, содержит постоянную и турбулентную составляющие. При этом постоянная составляющая характеризует основную концентрацию СО в выбросах автомобиля и является функцией от пространственных координат (x,y,z), максимальной концентрации оксида углерода, времени (t), скорости автомобиля и ветра (Va, Vb), направления ветра,  высоты расположения источника выбросов. Турбулентная составляющая, характеризующая газовую диффузию в турбулентном потоке автомобильного выхлопа, является функцией от координат (x,y,z), времени (t) и скорости автомобиля (Va).

Решение данного уравнения покажем в виде графика распределения концентрации оксида углерода по оси X при t = 0,02 c, Z = 0,05 м,  и разрезами по Y  (Y = Y0; Y = Y0+0,08; Y = Y0+0,16; Y = Y0+0,24). Где Y0=0,25 м – типовое расположение выхлопной трубы, Va=15 км/ч, Vb=0 м/с, при этом фоновая и локальная концентрация не учитывались. Для удобного отображения графики смещены друг относительно друга на единицу (рисунок 2).

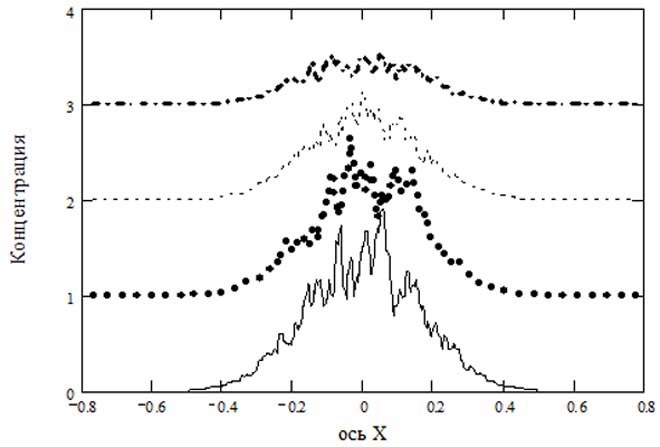
Рисунок 2 – Распределение концентрации оксида углерода по оси X при t = 0,02 c, Z = 0,05 м (Y = Y0 м – сплошная линия, Y = (Y0+0,08) м – точечная линия, Y = (Y0+0,16) м – пунктирная линия, Y = (Y0+0,24) м – штрихпунктирная линия)

Выводы: предложена математическая модель распределения концентрации СО в выбросах автомобильного транспорта. Получены качественные и количественные характеристики распределения СО в выхлопе автомобиля. Разработанная математическая модель позволяет определить с высокой вероятностью распределение концентрации примесей в газовом пространстве с учетом большинства влияющих величин. При определенных допущениях, а именно: скорость движения автомобиля положить равным нулю – математическая модель может быть адаптирована для определения краткосрочных выбросов ядовитых веществ от стационарных источников выбросов.

Перечень ссылок

1. Марчук Г. И. Математическое моделирование в проблеме окружающей среды/ Марчук Г. И. – М.: Наука, 1982. – 320 с.