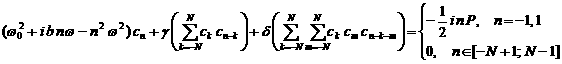Анастасова Е.А., Сухоруков М.Ю. Анализ субгармонических резонансов системы Дуффинга

Источник: «Компьютерный мониторинг и информационные технологии» — 2009 / Зборник материалов V Всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых «Компьютерный мониторинг и информационные технологии» (КМИТ - 2009). — Донецк, ДонНТУ — 2009, с. 365 - 367.

УДК 519.677

Анализ супергармонических резонансов системы Дуффинга

Анастасова Е.А. Сухоруков М.Ю.

Донецкий национальный технический университет

История развития динамики как науки предполагает ее разделение на три направления: прикладная, математическая и экспериментальная. Экспериментальная динамика является чрезвычайно важной отраслью науки. Это направление было обоснованно Г. Галилеем и приобрело наибольшее развитие благодаря открытиям Рэлея, Дуффинга и Ван-дер-Поля. Каждое новое технологическое открытие способствует развитию эмпирических методик в данной отрасли. Наиболее сильное влияние на исследования оказывает усовершенствование аналоговых и цифровых компьютеров, так как новые технологии позволяют решать более актуальные и сложные, с точки зрения вычислений, задачи в экспериментальной части исследований.

Георг Дуффинг, будучи выдающимся экспериментатором, уделял большое внимание изучению механических устройств, в частности исследованиям геометрических свойств динамических систем. Наиболее выдающимся его достижением стала теория колебаний [1].

Уравнение с характеристикой Дуффинга представляет собой нелинейное дифференциальное уравнение второго порядка:

(1)

Уравнение описывает затухающие колебания осциллятора с более сложным потенциалом, чем простые гармонические колебания. В физическом смысле, это такая модель как, например, пружинный маятник, жесткость которого не подчиняется в полной мере закону Гука.

Впервые о данном уравнении упоминается в 1918 году в работе Г. Дуффинга. В настоящее время оно широко используется в разных сферах науки:

- кинетические характеристики химических реакций;

- анализ плазм твердого тела;

- процессы в электрических цепях (ультрагармонические колебания в последовательно-, параллельно- резонансных цепях) [2];

- DRNN модель уравнения Дуффинга может быть использована при проектировании управляющих систем (англ. Dynamic recurrent neural network — DRNN);

- При анализе неавтономных систем [2].

Построение амплитудно-частотных характеристик (АЧХ) является одним из методов анализа динамических систем. Особенно этот метод важен при изучении периодических движений. В том числе, это актуально для анализа рассматриваемого уравнения (1). При этом неотъемлемым является применение функции «solve», которая позволяет находить множество решений системы нелинейных уравнений для построения АЧХ в среде Matlab.

Решение уравнения (1) производится численно — аналитически на базе метода гармонического баланса. Решение уравнения (1) ищем в виде:

(2)

где N — число учитываемых в решении гармоник, — комплексный коэффициент. , — комплексно сопряженные.

Коэффициенты тригонометрического разложения , образуются соотношениями:

(3)

Амплитуда n-ой гармоники ищется в виде:

(4)

Подставляя (2) в (1) и после выполнения преобразований (дифференцирования, возведения в степень и т.д.) и приравнивая коэффициенты при , получаем следующую систему уравнений:

(5)

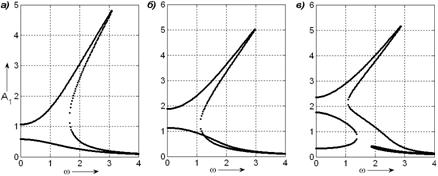
Дальнейший анализ системы (5) выполняется в среде Matlab, варьируя коэффициенты. В процессе выполнения поставленной задачи были получены АЧХ системы типа Дуффинга для одной гармоники. Для выявления влияния нелинейности на возбуждения супергармонических колебаний необходимо построение и анализ АЧХ решений системы (5) для гармоник более высокого порядка. Соотношения упругой силы и потенциальной энергии для колебаний описываемых (1) имеют вид:

(6)