Методы параллельного интегрирования жестких систем ОДУ

Автор Stig Skelboe

Перевод: Григорьева О.Н.

 

Аннотация

Эта статья представляет класс параллельных численных методов интегрирования для жестких систем обыкновенных дифференциальных уравнений, которые можно разбить на слабосвязанные подсистемы. Формулы называются обратноразностными дифференциальными формулами, и они получаются от классических формул путем приведения неявных частей к диагональной подсистеме. За исключением одной или нескольких подсистем, распределенных каждому процессору, информация должна быть заменена только после завершения шага, но не во время решения нелинейных алгебраических уравнений.

 

Основной акцент делается на формулу порядка 1, несвязную неявную формулу Эйлера. Доказано, что эта формула даже для широкого диапазона многошаговых представлений имеет асимптотическую глобальную ошибку, допускающую экстраполяцию. Кроме того,  представлены достаточные условия абсолютной устойчивости.

 

1 Введение

Определим систему ОДУ

  и   (1.1)

гдеявляется липшицевой  постоянной в у и  . Стабильные системы дифференциальных уравнений считаются жесткими, когда размер шага дискретизации путем явного метода интеграции ограничен по стабильности дискретизации, а не по точности. Эффективное численное интегрирование жестких систем по этой причине требует неявных интеграционных методов, например, неявных линейных многошаговых формул ​​или неявных методов Рунге-Кутта.

 

Для закрепления идеи, рассматриваем дискретизацию (1.1) при помощи обратной формулы Эйлера

           (1,2)

где и   для n = 1, 2,… Для того, чтобы вычислить новое дискретное приближение у_n от предыдущего у_n-1, неявная алгебраическая задача (1.2) должна быть решена с помощью, например, итерации Ньютона,

(1,3)

 

где и .

Распараллеливание обратной формулы Эйлера, следовательно, составляет распараллеливание (1,3), которое включает в себя параллельное вычисление f_n, J_n и параллельное решение систем линейных уравнений. Хотя эффективное распараллеливание f_n и J_n - часто вопрос тривиальный, эффективное параллельное решение систем линейных уравнений имеет доказанную трудность, особенно когда J_n  разреженный со случайной моделью ненулевых элементов.

 

Трудности, связанные с эффективным распараллеливанием (1,3) поторопили развитие альтернативных подходов, особенно колебательных релаксационных методов [1], где (1.1) разбивается на ряд связанных подсистем. Каждая подсистема проинтегрирована самостоятельно (тривиальное распараллеливание) на временном интервале. После завершения интеграционных изменений, решения (колебания) меняются и интегрирование на временном интервале повторяется с обновленными решениями от "других" подсистем. Релаксационный процесс повторяется до схождения в одной точке..

 

Колебательный релаксационный метод параллелизует хорошо и достигает значительной эффективности из разбиения исходной задачи на более мелкие подсистемы и от интегрирования каждой подсистемы с оптимальным выбором размера шага (многошаговой интеграции). Главная слабость колебательной релаксации – непосредственно итерационный процесс, который может страдать от медленной сходимости или даже расхождения. Другим недостатком является необходимость хранения колебаний, что существенно увеличивает требования к памяти.

 

Эта статья представляет два различных метода параллельного численного интегрирования

жестких систем обыкновенных дифференциальных уравнений. Они основаны на идеях  многошаговых интеграционных методов [2] и используют разбиение исходной задачи. Это разбиение позволяет разделение алгебраической системы на независимые задачи, являющиеся результатом дискретизации по обратной дифференциальной формуле.

 

2 монотонная макс-норм устойчивость.

 

Пусть исходная задача (1.1) будет разделена следующим образом,

 (2.1)

где и . При необходимости разбиение у будет указано явно, как в . Для подсистемы r, у_r называется локальной переменной интеграции и y_i; i≠r называются внешними переменными.

 

Следующее условие устойчивости, представленное в [2], играет решающую роль для стабильности несвязанных неявных методов интегрирования.

 

Определение: Монотонная макс-норм стабильность

 

Разделенная система (2.1) называется монотонно макс-норм устойчивой, если существуют нормы , такие, что

(2,2)

для всех  , где и выполняется следующее условие для

логарифмической макс-норм  матрицы (a_rj)

    (2.3)

Нормы, используемые в (2,2) могут быть связаны следующим образом, используя общую норму

Условие монотонной макс-норм устойчивости (2,2) является очень общим и ни

слишком интуитивным, ни слишком легко применимым на практике. Теорема 3 в [2] дает достаточные условия для монотонной макс-норм устойчивости разделенной системы. Эта теорема и связанные замечания дополняют общие определения монотонной макс-норм

стабильности.

 

3 Несвязный неявный метод Эйлера

Несвязный неявный метод Эйлера определяется следующим образом, где r-ая подсистема

Дискретизирована по обратной формуле Эйлера:

 (3,1)

где n = 1, 2,…, и внешние переменные  являются выпуклыми

комбинациями значений в для i≠r. Метод называется "несвязным", поскольку алгебраическая система, полученная в результате дискретизации, является разделенной на некоторое количество независимых алгебраических задач.

 

Несвязный неявный метод Эйлера особенно хорошо подходит для параллельного выполнения. Каждый процессор может решать одну или несколько систем, таких как (3,1) и информационный обмен с другими процессорами требуется только между решением шагов, где решение подсистемы меняется.

 

Выпуклости  являются необходимыми для устойчивости несвязного неявного метода Эйлера. Все выпуклые комбинации коэффициентом могут быть, вообще говоря, различными, но выпуклая комбинация, как правило, является одной из двух: либо экстра- или интерполяции нулевого порядка:

 где

или интерполяции первого порядка:

где

 

Пусть - последовательность выпуклых комбинаций  и пусть –последовательность выпуклых комбинаций где и - произвольные последовательности. Выпуклые комбинации и будут эквивалентны, если

для всех i,n) для всех i,n)

Устойчивость свойств несвязного неявного метода Эйлера описана в следующей теореме.

 

Теорема 1

Предположим, что разделенная система (2.1) является монотонно макс-норм устойчивой и рассмотрим любые два решения  ,, вычисленных по несвязному неявному методу Эйлера (3,1) с использованием тех же самых узловых точек и эквивалентные выпуклые комбинации и . Тогда

 

 

при условии, что  и  принадлежат

для всех r,n

Доказательство: теорема является следствием теоремы 4 в [2].

 

Есть два важных условия устойчивости результата теоремы 1, а именно: монотонная макс-норм устойчивость и выбор внешних переменных, которые должны быть выпуклыми комбинациями ранее вычисленных компонентов решения.

 

Следующая теорема является необходимой для оценки глобальной погрешности несвязных неявных методов Эйлера.

 

Теорема 2

Пусть (3,1) определяет функцию г для всех r = 1, 2,…, q и n = 1, 2,…такую, что

(3.2)

Предположим, что разделенная система (2.1) монотонно макс-норм устойчива, и что

 и что f_r непрерывна в y_r. Тогда  существует и   является липшицевой постоянной для у-переменных, где  с константой Липшица 1 для  y_r,n и для

 

Доказательство:

Монотонная устойчивость макс-норм предполагает,

где

Согласно [3] леммы 2, (3,1) может быть решен однозначно для y_r,n и y_r,n являющимся  непрерывной функцией Липшица от  y_r,n-1 с константой Липшица

 

Для u_r,n-1= v_r,n-1 и u_j и v_j, соответственно, замененных для , монотонная макс-норм устойчивость приводит к соотношению:

 

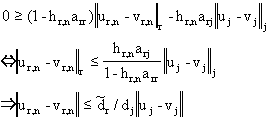
Несвязный неявный метод Эйлера, определенный в (3,1), может быть использован с полностью произвольно выбранным размером шага и все еще сохранять устойчивость, когда условия теоремы 1 выполнены. Однако для получения достаточной точности требуются ограничения на размер шага. Такие ограничения могут быть представлены через многоскоростные соединения шагов, два различных примера которых приведены ниже.

 

Определение: Основной составной шаг

Для r = 1, 2,…q определим составной шаг на интервале [t₀, t₀ + Nh]:

при n = 1, 2,…N / p_r, где p_r делит N.

 

Основной составной шаг, а также самая медленная первая составляющая шага, установленная ниже, определены для интервале [t₀, t₀ + Nh]. Это сделано для упрощения записи, и определение составных шагов легко распространяются на любой интервал шириной Nh. Любой численный алгоритм интегрирования на основе этих методов будет в целом использовать последовательность составных шагов. Составной шаг имеет некоторое сходство с шагом метода Рунге-Кутта.

 

Основной составной шаг использует простейшую выпуклую комбинацию, соответствующую экстраполяции нулевого порядка. Хотя порядок точности не улучшлся, абсолютная точность будет, вообще говоря, лучше, когда линейная интерполяция используется всякий раз, когда это возможно. Это реальность самой медленной первой составляющей шага:

 

Определение: Самая медленная первая составляющая шага

Самый медленный составной шаг определяется рекурсивно на интервале [t₀, t₀ + Nh].

Подсистемы были определены так, что они являются интегрируемыми при использовании все более и более уменьшающегося размера шага.

 

Рисунок 1: Пример распределения размера шага для самого медленного первого составного шага.

 

Подсистема r является интегрируемой с размером шага p_rh, где p_r <=p_r-1 , p₁ =N, p₀=p₁ и p_r делит p_r-1

Общее рекурсивное определение для r = 1, 2,…,q-1 следующее:

p_r-1 / p_r  шаги подсистемы вычисляются как один шаг подсистемы r, следующий за

p_r / p_r+1 шагом подсистемы r +1, затем еще один шаг к подсистемы r, и т.д.

 

Подсистема 1 является интегрируемой следующим образом:

(3.3)

Далее следуют подсистемы 2, 3,…q, как указано в рекурсии. Используются следующие общие формулы:

при n = 1, 2,…N / p_r Выпуклые комбинации, определены следующим образом:

для n = 1, 2,…r-1. ( обозначает округление к нулю)

Самый медленный составной шаг и включение интерполяции проиллюстрировано с помощью рис.1. Первый y[1, p1] вычисляется с использованием y[2,0] и у[3, 0]. Тогда один шаг подсистемы 2 вычисляется линейной интерполяцией между (y[1, 0], y[1, p1]) и с использованием y[3; 0]. Теперь следуют p2/p3 (= 4) шаги подсистемы 3, интерполирующиеся линейно между парами (y[1,0], y[1,p1]) и (у[2,0], y[2,p2]). Максимальная глубина рекурсии теперь достигнута и вычисляется еще один шаг подсистемы 2, p2/p3 больше шагов подсистемы 3 и т. д.

Основной составной шаг сохраняет параллельность несвязного неявного метода Эйлера, в то время как самый медленный первый составной шаг фиксирует последовательность вычисления, которая снижает параллельность.

Слегка модифицированная версия самого медленного первого составного шага может быть представлена полностью параллельно на P процессорах в следующем случае: первые P подсистем являются интегрируемыми при использовании того же размера шага p[1]h=p[2]h=…=p[p]h, следующие P подсистем являются интегрируемыми при использовании шага  размером р[p +1]h = р[p +2]h =… = р[2p]h, и т.д.