Сегментация растрового изображения организована однопроходным целочисленным рекуррентным алгоритмом SPIRAL (Single-Pass Integer Recurrent Algorithm Line) через подбор моделей пучка дискретных прямых Брезенхейма, в диапазоне угла наклона от 0 до 90, с помощью аккумуляторных массивов Хоха (Hough Transform) и видоизмененным, с помощью хеш-функции, цепным кодом Фримана (Freeman). Алгоритм сегментации разработан для реализации простым цифровым устрой- ством на регистрах памяти, сумматорах и элементах задержки.


Введение

В работе речь идет о двухмерном дискретном пространстве и сегментации его прямоугольной области через подбор модели дискретной прямой. Этот факт не исключает использование схемы сегментации для трехмерного дискретного пространства после соответствующей модификации.
Практическое открытие не улучшает существующую теорию распознавания образов, а качественно изменяет принципы организации вычислительного процесса, что открывает широкие возможности по применению метода в задачах искусственного интеллекта.
Сегментация растрового изображения заключается в нахождении геометрических образов. Простые образы представлены геометрическими примитивами: прямой линией, окружностью. Сложные образы представлены геометрическими фигурами: многоугольниками, кривыми линиями. Аппроксимация сложного образа основывается на использовании простых образов геометрических примитивов. В работе [1] показано, что четырьмя прямыми линиями можно аппроксимировать четырехугольник. Как утверждает специалист новой профессии трендсеттер голландка Ли Эделькорт: искусственно созданные вещи легко опознаются по прямым линиям и углам в отличие от объектов, созданных природой, имеющих плавные формы [2]. Компьютерный шрифт текста, штрих-код товара, автомобильный номер, маркер расширенной реальности ARGET [3] — вот тот неполный перечень искусственно созданных геометрических форм, основывающихся на прямых линиях и углах. Распознавание приведенных графических образов начинается с сегментации растрового изображения в виде нахождения отрезков прямых линий. Существуют два подхода сегментации, не отличающиеся на первый взгляд друг от друга, но каждый из которых включает множество методов.
Первый подход — сегментация растрового изображения через подбор моделей. Подбор модели — это группировка пикселей, соответствующих некоторой модели, причем модель определена явно и в ней могут фигурировать связи не только на уровне переходов между отдельными пикселями, но и на более высоком уровне [4, с. 459]. Например: если подбираемая модель — прямая линия, то задано конкретное значение угла наклона и смещение. Результат сегментации — формируется список пикселей, принадлежащих модели. Организация вычислительного процесса методом подбора представлена преобразованием Хоха (HT — Hough transform). Например, для модели прямой преобразование HT объясняет: 1) что является прямой, если есть точки, принадлежащие прямой; 2) какие точки принадлежат каким прямым; 3) сколько должно быть прямых. На практике ответы получаются редко. Базовое действие алгоритма сегментации методом HT: берется каждый пиксель изображения и определяются все структуры, которые могут проходить через этот пиксель.
Второй подход — сегментация растрового изображения через обнаружение моделей. Обнаружение моделей — это когда пиксели собираются в кластеры, которые «выглядят подобно» знакомой геометрической конфигурации, а затем дальнейший анализ определяет конкретные значения параметров модели. Обнаружение нельзя сделать, изучив только попарные отношения между пикселями. Поэтому необходимо исследовать некоторые свойства пикселей, определяемых заданной закономерностью, и принять какой-то критерий хорошего соответствия. Метод наименьших квадратов позволяет определить параметры математической модели, которая наилучшим образом аппроксимирует наблюдаемые данные [5, с. 403].
Различия в результатах применения методов имеют системный характер. Системный критерий отбора кандидатов на соответствие модели определяется возможностью распознавания. Например: проблема дискретизации влияет на любой определитель прямых линий, который оценивает направление по малой окрестности данного пикселя. Растровые отрезки не являются прямолинейными. Диагональные отрезки в действительности состоят из последовательности горизонтальных и вертикальных сегментов. Если при вычислении угла используется слишком маленькая окрестность, то вместо длинного диагонального отрезка будет обнаружено большое количество мелких горизонтальных и вертикальных отрезков [5, с. 402]. Поэтому очень часто имеется неудовлетворительный результат распознавания.
Ошибка закладывается на первичном этапе обработки входных данных, когда сегментация создает ложные системные свойства среди множества найденных графических примитивов. Способ организации вычислений методов сегментации является скрытой частью критерия отбора. Он и даёт искажение результата. Поэтому важно подчинять вычислительный способ обработки первичных данных критерию сегментации. Организация вычислений в существующих методах распознавания диктует свои условия формулировки критерию отбора кандидата на соответствие модели. В противоположном случае, при жесткой формулировке критерия, вычислительный процесс дает такие погрешности, что нивелируется результат сегментации.
Вывод: организация вычислений по сегментации 2D-пространства должна являться частью критерия отбора прямых и составлять с ним единую систему. Необходимо очень взвешенно подходить к разработке критерия отбора кандидата на соответствие модели – максимально приблизить к задаче распознавания и её дальнейшего этапа — анализа сложных фигур. Такой подход был заложен в рассматриваемую схему сегментации SPIRAL (Single-Pass Integer Recurrent Algorithm Line). Подход SPIRAL является обобщением частного случая подходов подбора и обнаружения прямых линий для задачи распознавания маркеров расширенной реальности ARGET.


Постановка задачи

Согласно правилам размещения маркеров в предложении ARGET [1], [3] для распознавания четырехугольной формы одного маркера на бинарном контурном изображении необходимо проложить прямолинейный фарватер между двумя маркерами.
Рамка цвета фона вокруг маркера является уникальным отличием кода ARGET от кода ARTag [3]. Зазор между двумя маркерами цвета фона в несколько пикселей позволяет аппроксимировать границу маркера дискретной моделью прямой линии. Пространство вокруг маркера, в виде четырехугольной рамки цвета фона, служит задаче сегментирования его границ. За счёт рамки графический образ маркера ARGET имеет максимальную изобразительную простоту. Фактически на плоскости изображения можно поместить большее количество маркеров ARGET, чем маркеров ARTag, и при этом получить значительный выигрыш в быстродействии алгоритмов распознавания.
Зазор в виде полосы образует мыслимую трубу, по прямолинейному фарватеру которой движется дискретная линия. Это важное допущение делает возможной разработку схемы целочисленного однопроходного подбора прямой линии цвета фона SPIRAL. Для обнаружения прямых линий цвета объекта данная схема имеет ограничения. Координаты точек дискретной прямой образуют траекторию движения по трубе. Труба как структура данных описывается списком, индексы элементов которого связаны рекуррентной формулой. Рекуррентный характер заполнения трубы точками дискретной прямой был доказан компьютерным экспериментом в работе [1].
Использование минимального количества изобразительных элементов кода ARGET делает его графическим языком роботов [6], [7]. Ввиду однозначной простоты графического символа маркера достигается максимальное быстродействие алгоритмов распознавания как программной, так и аппаратной реализации. Так как маркеры ARGET прямоугольной формы, то система технического зрения робота сегментирует изображение на прямые линии уникальным методом SPIRAL.


Дискретное пространство

Дискретное пространство представляет собой структурированный массив информации. В компьютерной графике таким массивом информации будут: графические структуры сцены и непосредственное представление изображения на экране [8, с. 10]. Например, цифровая фотография является двухмерным массивом, что соответствует прямоугольной области дискретного 2D-пространства. В математической модели цифрового изображения выполняется переход от непрерывного представления кривой к дискретному представлению. Потому что считывающий элемент фотокамеры осуществляет пространственную дискретизацию на плоскости [9, с. 332]. Выбранная математическая модель цифрового изображения необходима для отображения на экран монитора и осмысленного восприятия глазом человека. Поэтому поверхность визуализации представляет собой мозаичный экран, имеющий вид регулярной прямоугольной сетки, в декартовой системе координат, где любой паре целых чисел (X, Y) соответствует элементарная квадратная площадка, называемая пикселем [8, с. 10]. Элементарная квадратная площадка, в отображении результатов компьютерного моделирования, изображается закрашенной фигурой на дискретной сетке экрана. Закрашенную фигуру уместно назвать плиткой. В доказательстве постулатов геометрии, перемещая четырехугольную фигуру, составленную из двух прямоугольных треугольников, можно «замостить» плоскость равными прямоугольниками [10, с. 27]. Поэтому «замостить плиткой» отрезок прямой линии на плоскости – это мозаично расположить пиксели на дискретной сетке 2D-пространства, что наилучшим образом аппроксимирует непрерывное представление прямой.
Вывод: математические модели, методы и алгоритмы [8], [9] синтеза растровых изображений идеально подойдут для сегментации ограниченного дискретного 2D-пространства робототехническими системами.


Математическая модель дискретной прямой

Решающие правила в форме неравенств и индексные преобразования в форме целочисленных полиномов являются математическим аппаратом дискретных моделей. Отрезок дискретной линии — это последовательный набор ячеек дискретного пространства, когда два элемента набора находятся в отношении соседства. Закономерность соседства описывается решающим правилом связности. Параметрическая математическая модель ячейки дискретного пространства основывается на нумерации целочисленным индексом в некоторой системе различающих признаков. Система основывается на целочисленном шаге дискретизации и однородном характере отношений между ячейками пространства. Однородная организация пространства состоит в целочисленной формуле преобразования индексов. В однородной среде индексы двух ячеек отличаются на некоторую целочисленную величину I. Величина I является параметром правила связности. Если величина I совпадает с шагом дискретизации пространства, то соседство ячеек очевидно. Например, для одномерной организации пространства решающее правило связности имеет следующий вид: i(a) - i(b) <= I. При I = 1 индексы соседних ячеек должны отличаться на единицу. Организация классических d-мерных (d >= 1) однородных структур представляет собой множество всех d-мерных кортежей — целочисленную решетку в евклидовом E^d-пространстве, элементы которой служат для пространственной идентификации ячейки [11, с. 61].
Способ организации однородного 2D-пространства, в соответствии с прави- лами представления правильных точечных систем второго порядка, определяется по окрестности размещения ячеек [12, с. 165]. В окрестности Мура связность ячейки-ядра равна восьми (рис. 1а), а в окрестности фон Неймана связность ячейки-ядра равна четырем (рис. 1б).


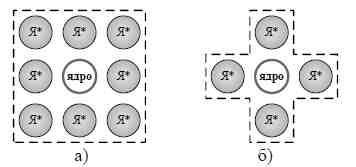
Рисунок 1 — Окрестности размещения ячеек однородных структур: а) окрестности Мура; б) окрестности фон Неймана
Решающее правило для 4-связной области фон Неймана: ячейки a и b считаются соседними, если либо их индекс i первого параметра, либо их индекс j второго параметра отличаются на I [13, с. 156]. Имеем следующее неравенство:

|i(a) - i(b)| - |j(a) - j(b)| <= I

Понятие отрезка дискретной прямой базируется на понятии связности. Растровый алгоритм построения дискретной прямой Брезенхейма [13] модифицируем для представления модели отрезка прямой в алгоритме сегментации SPIRAL. Четырехсвязная схема дискретной прямой линии Брезенхейма (рис. 2а) может быть представлена усеченной окрестностью фон Неймана (рис. 2б).


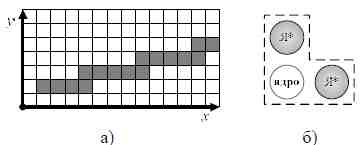
Рисунок 2 — Прямая Брезенхейма: а) представление дискретной прямой; б) модель окрестности
Вывод: четырехсвязная прямая линия Брезенхейма имеет только два направления соседства в инкрементных методах построения дискретной прямой (рис. 2б). Таким образом, для представления в памяти компьютера четырехсвязной прямой Брезенхейма достаточно двух значений направления изменения координат.


Представление дискретной прямой циклическим цепным кодом

В ограниченном 2D-пространстве четырехсвязная прямая Брезенхейма имеет свойство повторять свою геометрическую форму. На рис. 3 построена дискретная прямая с углом наклона 13 градусов, повторяющая свою геометрическую форму с периодом dx, для области размером 160 точек по ширине и 120 точек по высоте


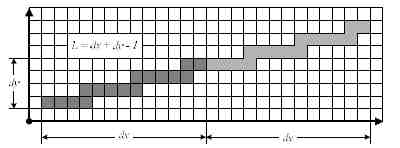
Рисунок 3 — Периодическое повторение геометрической формы прямой.
Из рис. 3 видно, что количество итераций замощения дискретного пространства 4-связной прямой линией определяется по формуле (1)

L = dx + dy – 1. (1)

В компьютерной графике для представления в памяти компьютера дискретных контуров графических фигур применяется цепной код Фримана [4], [9]. Математическая модель цепного кода используется для приближенного представления графических данных. Цепной код помогает выявить в данных важные структурные свойства фигур. Поэтому используем цепной код для представления данных о линии. Цепной код Фримана сжимает поток графических данных о контуре фигуры по схеме кодирования, показанной на рис. 4а. Направление изменения координат контура фигуры кодируется десятичным числом. На рис. 4б показан контур фигуры, имеющей представление цепным кодом в виде последовательности чисел «2-0-1-2-1-7-0-6-7-7».


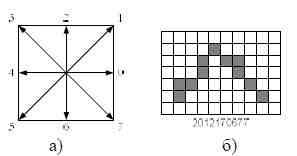
Рисунок 4 — Цепное кодирование Фримана: а) схема кодирования; б) контур фигуры.
Для представления цепным кодом используемой прямой линии достаточно два направления в схеме кодирования Фримана. Направление вправо, а это приращение по абсциссе, обозначим числом 0. Направление вверх, а это приращение по ординате, обозначим числом 1 (рис. 5а). На рис. 5б показан контур прямой линии с углом наклона 13 градусов, который можно представить измененным по новой схеме (рис. 5а) цепным кодом «1-1-1-0-1-1-1-1-0-1-1-1-1-0-1». Прямая линия, приведенная на рис. 3, имеет цепной код «1-1-1-0-1-1-1-1-0-1-1-1-1-0-1».


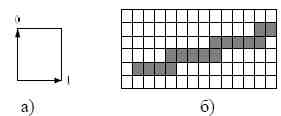
Рисунок 5 — Цепной код прямой линии: а) схема кодирования прямой; б) прямая линия.
Для построения алгоритма генерации цепного кода прямой Брезенхейма необходимо определить её максимальную длину в ограниченном 2D-пространстве. Согласно формуле (1) необходимо определить точку пересечения прямой линии с границей дискретной области. На рис. 6а показан случай, когда прямая линия с углом наклона u является гипотенузой AB с противолежащим катетом AC. Длина dx0 прилежащего катета CB больше ширины m области 2D-пространства. Тогда приращение по ординате dy прямой максимальной длины будет соответствовать противолежащему катету A'C', вычисленному по значению n прилежащего катета B'C'.


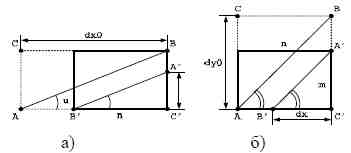
Рисунок 6 — Точки пересечения прямой с границей 2D-пространства: а) пересечение с ординатой; б) пересечение с абсциссой.
На рис. 6б показано, что приращение по абсциссе прямой A'B' с максимальной длиной вычисляется через высоту m области 2D-пространства.
Определив максимальную длину прямой Брезенхейма, которая зависит от угла наклона, сгенерируем её циклический код в виде массива E. На рис. 7 показаны начальные ячейки массива E для прямой линии с углом наклона 14 градусов. На практике массив E содержит повторяющиеся ячейки. Создадим массив ETR размером EN, который будет содержать компактное представление циклического кода прямой. На рис. 7 показано, что первый элемент массива ETR встречается в массиве E с перио- дичностью EN.


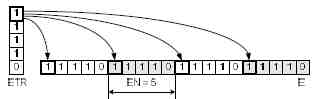
Рисунок 7 — Рабочие массивы цепного представления прямой.
Для обнаружения повторяющейся последовательности ячеек в массиве E разработаем схему гаммирования Gamma(ETR, E):
1. Заносим первый элемент E в первую ячейку ETR и устанавливаем EN = 1.
2. Из элементов ETR строим гамму, длиной массива E.
3. Сопоставляем элементы массива E и гаммированной последовательности.
Если они равны, то компактное представление создано, иначе добавляем из E новый элемент в массив ETR.
На рис. 8 показано несоответствие элементов массива E гаммированной последовательности Gamma(ETR, E).


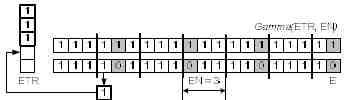
Рисунок 8 — Поиск компактного представления цепного кода.
Для пучка прямых, с углом наклона u от 0 до 90 градусов, построим компактный цепной код, в виде массивов ETR[u, i]. Длину последовательности i сохраним в массив EN[u].
Вычисление координат прямой Брезенхейма будем осуществлять с помощью хеш-функции. Для использования операции mod в качестве хеш-функции необходимо последний элемент массива ETR поставить в начале списка. Полученный новый список EE будем называть циклическим цепным кодом (ЦЦК). Нумерация массива EE начинается с нуля. Прямая линия, изображенная на рис. 3, имеет следующий ЦЦК «111101111011110». Реконструкция цепного кода отрезка прямой линии Брезенхейма осуществляется по формуле:

EEu,i mod ENu. (2)

Вывод: ЦЦК прямой линии и хеш-функция (2) представляют порождающую процедуру отрезка дискретной прямой.


Мозаичное замощение дискретного 2D-пространства семейством прямых

В обработке структур дискретного пространства применяют растровую систему координат. Область ограниченного 2D-пространства, размером m строк, n столбцов, разместим с координаты (1,1).
Через ограниченную область пространства может проходить семейство прямых. Семейство прямых – это прямые линии с одинаковым углом наклона, но разными смещениями. Пучок прямых – это все многообразие прямых, проходящих через текущую точку пространства.
Если область пространства мозаично замостить семейством прямых линий для каждого угла наклона, то из полученного множества семейств прямых можно сформировать пучок прямых.
Процедура мозаичного замощения ограниченного пространства множеством семейств прямых имеет два случая. Пучок прямых линий, в диапазоне от 0 до 90 градусов, делится на два октантных угла [14, с. 36]. Руководствуясь неравенством (рис. 9а), разобьем линии пучка на две группы. Для построения группы семейства линий 1-го октантного угла используем следующую стратегию (рис. 9б).
В растровой системе координат, используя ЦЦК прямой, с заданным углом наклона u и из первой октантной группы, построим семейства линий. Начало первой линии FD – это точка F, которая размещена на линии правой границы области замощения и удалена от оси абсцисс на расстояние 5·(n + m). Используя ЦЦК прямой, рассчитаем координаты точек траектории линии FD. Пересечение линии FD с границей области произойдёт в точке A. Условием останова генерации координат будет: пересечение линии FD с осью Ox в точке D. Координаты точки A сохраним в массив XN[i,u], i = 1..n. Далее, уменьшив ординату точки F на шаг dy, построим следующую линию семейства и запомним её координату пересечения с границей области. Если линия пересекла правую границу области, как, например, в точке E, то координаты занести в массив YM[j,u], j = 1..m. Цикл продолжать до обнуления ординаты новой точки F.
Координаты траекторий отрезков, проходящих в плоскости ограниченного 2D-пространства, например, отрезок AB, занести в массив F[i,j,u], i = 1..n, j = 1..m. Массив F позволит проанализировать частоту прохождения отрезков одного семейства через точку области.


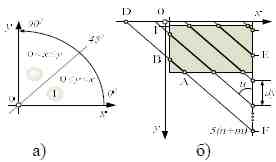
Рисунок 9 — Мозаичное замощение линиями группы 1-го октантного угла: а) октантный угол; б) пучок линий 1-го октантного угла.
Для 2-й октантной группы линий точка F расположена на оси Ox и удалена от начала координат на расстояние 5·(n + m). В изложенной стратегии мозаичного замощения для семейства прямых с углом наклона u = 46..90 будем использовать углы наклона u' = 90 – u. Условием останова генерации траектории прямой будет её пересечение с нижней границей области в точках B или D. Условием останова генерации семейства прямых линий будет обнуление абсциссы новой точки F (рис. 10). В массив F координаты траектории отрезков заносим под индексом u, а не под индексом u'.


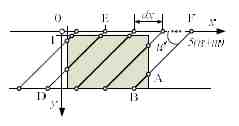
Рисунок 10 — Мозаичное замощение линиями группы 2-го октантного угла.
Для анализа результатов замощения используем массив F: по сохраненным координатам точек построим изображение. На рис. 11а приведен результат замощения семейством линий области 34 × 28, с углом наклона 16 градусов и шагом дискретизации dy = 1. Темные точки обозначают прохождение двух линий через точку.


Рисунок 11 — Результаты мозаичного замощения области 34 × 28:
а) <16 градусов, 34 × 28, шаг dy = 1>; б) <67 градусов, 34 × 28, шаг dx = 1>; в) <16 градусов, 34 × 28, шаг dy = 3>; г) <67 градусов, 34 × 28, шаг dx = 3>.
На рис. 11а видно, что все точки области закрашены: через точку прошло не менее одной, но не более двух линий. Это важное основание для построения рекуррентного алгоритма подбора прямых. На рис. 11б построено семейство линий с углом наклона 67 градусов. На рис. 11в, 11г линии построены с шагом 3 и не пересекаются между собой, но размечены темным цветом для наглядности.


Схема графической сети

В большинстве случаев обработка графической информации основывается на принципе разделения алгоритма на две части: модуль предобработки и ядро использования. По аналогии такой подход применяется в искусственных нейронных сетях с обучением (ИНС). В общем случае сетевые модели имитационного моделирования, такие, как сети Петри или ИНС, сначала конфигурируют, а затем используют. В сетевой модели соблюдается баланс между быстродействием элементарных вычислительных операций и объемом используемой памяти. Всё, что можно рассчитать предварительно, закладывается в память сети, а пересчет нового состояния сводится к нематематическим рекуррентным операциям манипуляций над состояниями конечного автомата. Такой принцип синтеза быстродействующей имитационной модели заложен в рассматриваемый подход SPIRAL.
Как правило, базовым графическим примитивом системы технического зрения является прямая линия. Система распознавания графических примитивов оперирует большим объёмом однородных элементов и статистическими показателями, которые не сложно математически вычислить. Простота математических формул вычисления статистических показателей обусловлена применяемой формой окрестности однородного элемента. Используемая форма пространственного соседства однородных элементов дискретного 2D-пространства позволяет реализовывать рекуррентные операции по их обработке. Поэтому для проектирования алгоритма обнаружения прямых линий подходит сетевой вид представления имитационной модели обработки графических данных. Организацию процесса синтеза распознающего автомата назовём графической сетью.
Имитационная модель обнаружения прямой линии на плоскости имеет классическую схему. Схема реализует три этапа функционирования графической сети: инициализация (Init), работа (Work), повторение (Repeat).
Этап инициализации – это занесение параметров конфигурации в рабочие массивы состояния сети. Этап работы – это один шаг моделирования, за который изменяется состояние сети и принимается решение. Этап повторения – это обратная связь, занесение предыдущего состояния в рабочие массивы сети. Структура графической сети имеет следующие элементы <YM, XN, A> (рис. 12). Начальное состояние сети YM содержит ненулевые состояния перехода к следующей точке траектории прямой линии t0. Верхний уровень организации массива YM соответствует одному вертикальному столбцу области дискретного 2D-пространства размером m. Внешнее воздействие XN содержит начальные точки траекторий прямых линий, пересекающих нижнюю границу дискретной области, что соответствует одной горизонтальной строке этой области, размером n. Организация массива XN соответствует массиву YM. Рабочий массив состояний A содержит аккумуляторные ячейки Хоха (Houge Transform) и ячейки особого состояния перехода t к следующей точке траектории прямой линии. Аккумуляторные ячейки содержат текущие значения статистических показателей распознавания и используются для обнаружения отрезков прямых линий. На первом шаге моделирования аккумуляторные ячейки заполняются нулевыми значениями, а ячейки особого состояния инициализируются значениями из YM. Размер верхнего уровня массива A соответствует одному вертикальному столбцу дискретной области 2D-пространства.


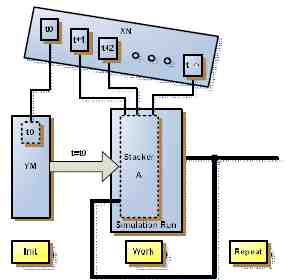
Рисунок 12 — Схема графической сети.
Особенностью работы графической сети является то, что на этапе работы на каждом новом шаге моделирования i из внешнего мира XN поступает новое состояние t + i, которое заносится только в одну ячейку особого состояния массива A.


Процесс синтеза конфигурации графической сети

Схема синтеза конфигурации графической сети представлена на рис. 13. Синтез конфигурации выполняется один раз при создании системы технического зрения по заданным параметрам разрешения видеокамеры. Ограниченная область дискретного 2D-пространства соответствует размеру получаемого камерой растрового изображения. На втором этапе задается список углов наклона для множества семейств прямых. Схема SPІRAL работает с углами в диапазоне от 0 до 90 градусов. В компьютерном эксперименте диапазон был разбит с шагом 1 градус. Для увеличения быстродействия алгоритма SPІRAL для некоторых прикладных задач можно задавать шаг больше единицы. Для большей точности угла наклона подбираемой прямой шаг можно задавать дробный, а алгоритм всё равно останется целочисленным. На третьем этапе по схеме рис. 6 и формуле (1) вычисляем максимальную длину дискретных линий Брезенхейма. На четвертом этапе генерируем по одной прямой из каждого семейства максимальной длины. На пятом этапе геометрическую форму полученных линий кодируем цепным кодом Фримана согласно схеме, представленной на рис. 5а. На шестом этапе циклический код прямой сжимаем хешированием. На седьмом этапе сжатые данные преобразовываем в циклический цепной код прямой (ЦЦК), переставив последний элемент в начало списка. Модель ЦЦК используется для компьютерной генерации прямой по формуле (2). На восьмом этапе проводим компьютерный эксперимент для нахождения координат F множества семейств прямых, построенных по модели ЦЦК, которые мозаично замос- тили заданную область. На девятом этапе в массиве F выявляем координаты точек, пересекающих нижнюю границу области и правую границу области. На девятом этапе найденные начальные точки разносятся по массивам XN и YM. Соответственно XN содержит номер отсчета ЦЦК прямой, пересекающей нижнюю границу, а массив YM содержит номер отсчета, в нотации ЦЦК, точки пересечения прямой с правой границей области. Десятый этап, приведенный на рис. 13, требует детального описания.


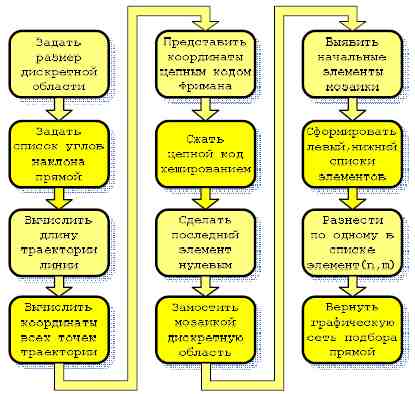
Рисунок 13 — Синтез конфигурации графической сети.
графической сети является то, что на каждой новой итерации моделирования один начальный элемент из XN заносится в рабочий массив A, а массив A первоначально инициализируется значениями из YM. Поэтому возникает коллизия с элементом (n, m) массива F: при слиянии элемента XN(n) с элементом YM(m) в ячейке A(m) дублируются координаты начальных точек прямых. Поэтому для разрешения коллизии разнесем начальные точки элемента F(n, m) по одному в массивы XN(n) и YM(m), как показано на рис. 14.


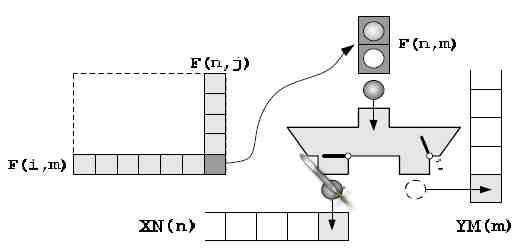
Рисунок 14 — Разрешение коллизии для элемента F(n, m).
Вывод: выполнив десять этапов проектирования, получим конфигурацию графической сети <EE, EN, XN, YM> для заданной области 2D-пространства.


Общая схема имитационного моделирования графической сети

Главная особенность графической сети заключается в свойствах мозаичного замощения поверхности ограниченной области 2D-пространства. Семейство линий посещает все точки дискретного пространства, но при этом одновременно не более двух прямых. Это важное свойство можно проиллюстрировать рис. 15.


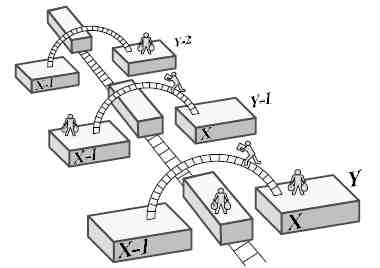
Рисунок 15 — Принцип моделирования графической сетью дискретной прямой.
Рекуррентная процедура может оперировать текущим состоянием графической сети для определения нового состояния сети. При этом переход (Lifting) в новое состояние осуществляется двумя путями: сдвиг влево или сдвиг вверх. Переход влево — это имитационное моделирование на следующем шаге итерации. Переход вверх требует только одну дополнительную ячейку рабочего массива A на той же итерации моделирования.
Схематически, на элементах памяти, можно показать реализацию принципа моделирования графической сетью реконструкции траектории прямой линии (рис. 16).


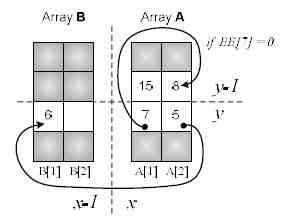
Рисунок 16 — Пример работы сети SPIRAL на элементах памяти.
Переход в пределах одной сессии моделирования показан для ячейки A[1, y] со значением номера отсчета ЦЦК 7. Переход из ячейки A[1, y] в ячейку A[1, y-1] невозможен, так как она занята, тогда задействуем запасную ячейку A[2, y]. Условие перехода определяется направлением движения прямой представленного ЦЦК в виде элемента массива EE [7]. В ячейку A[2, y-1] заносится инкрементированное значение номера отсчета следующей точки траектории, в нотации ЦЦК.
Переход на новое состояние из дополнительной ячейки A[2, y] осуществляется влево и требует запоминания состояния сети в массиве B. Структура массива B идентична структуре массива A. На новом шаге моделирования рабочий массив А инициализируется значениями из массива B.
Конкретная реализация алгоритма работы графической сети будет зависеть от используемой схемы массивов памяти. Классическая схема имитационного моделирования оперирует двумя рабочими массивами особых состояний A и B. Массив A содержит текущие состояния графической сети и используется для обнаружения прямых линий, а массив B содержит значения сети для следующего шага моделирования.
Обобщенный алгоритм работы графической сети представлен в виде блок-схемы на рис. 17. В алгоритме три цикла: по изменению столбца дискретного пространства, по изменению строки дискретного пространства, по изменению угла наклона пучка прямых. Новый шаг моделирования соответствует верхнему циклу по столбцам. Локальный шаг изменения состояния сети в одной итерации соответствует первому вложенному циклу по строкам. Третий цикл по углу наклона для каждой точки 2D-пространства подбирает модели прямых линий простыми операциями манипуляции над ЦЦК. Перед изменением состояния рабочих массивов сети выполняется процедура принятия решения об обнаружении отрезка.


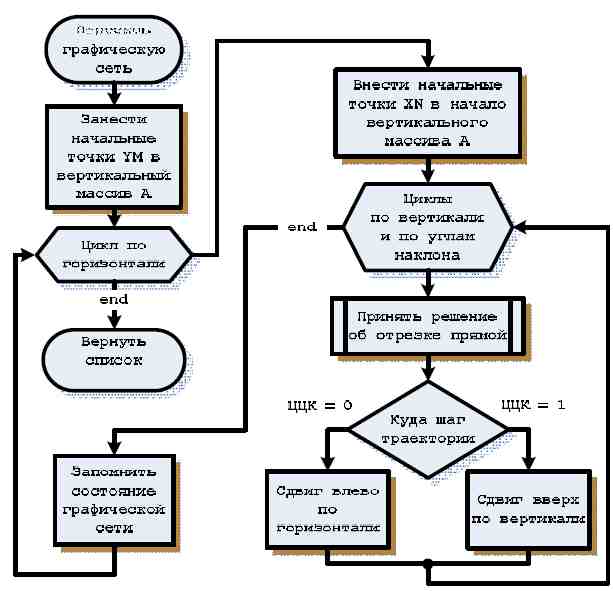
Рисунок 17 — Блок-схема работы графической сети.
Алгоритм, использующий классический стиль моделирования графической сети, назовем A2, так как дополнительная ячейка массива А[2] используется только один раз при продвижении вверх. Компьютерный эксперимент алгоритма A2 показал, что в массиве B находится всегда не более одного состояния сети. Тогда из массивов A и B можно убрать один столбец, заменив использованием их в алгоритме одним массивом C[u] небольшой размерности u = 0…90. В алгоритме A2 для массивов A и B необходимо учитывать количество занятых ячеек. Если обозначить признаком –1, что ячейка массива A, B или C свободна, то можно реализовать алгоритм, использующий повторяющиеся фрагменты кода. Такой алгоритм назовём C1.
Вывод: алгоритм A2 можно адаптировать для обнаружения восьмисвязных прямых линий Брезенхейма, алгоритм C1 оптимизирован для минимизации используемой памяти и увеличения быстродействия.


Компактная версия алгоритма A2 графической сети SPIRAL

На рис. 18 приведена блок-схема алгоритма A2. Входными данными алгоритма являются: конфигурация графической сети <EE, EN, XN, YM> и массив черно-белого изображения P, где значение 0 соответствует цвету фона, а значение 1 соответствует значению цвета объекта. Массив AA содержит аккумуляторные ячейки Хоха, которые содержат сумму пикселей, соответствующих дискретной модели четырехсвязной линии Брезенхейма. Если пиксель Px,y = 0, то ячейка массива AA обнуляется по формуле AAx-1 = Px,y ( AAx-1 + 1). Ячейки A0,y,u и B0,y,u содержат текущее количество занятых ячеек в строке массива A. Массив L содержит список координат начала найденных отрезков и их длину.


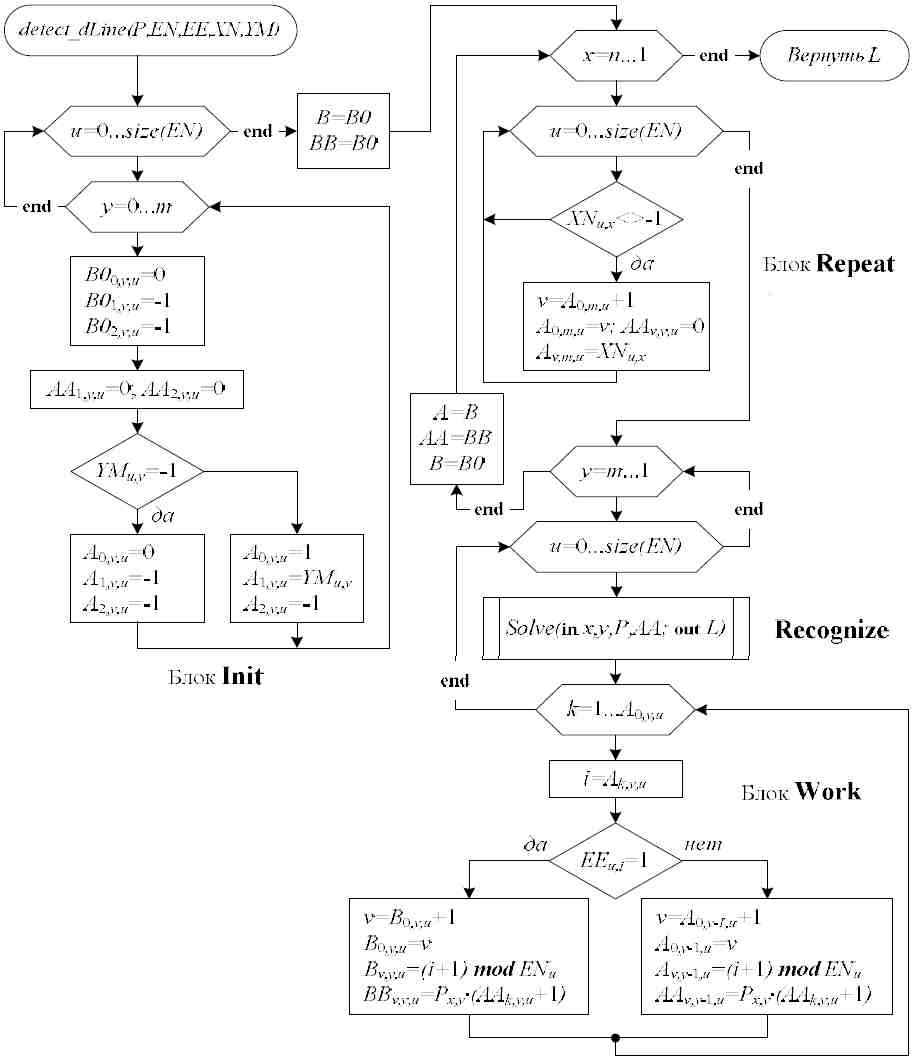
Рисунок 18 — Блок-схема алгоритма A2.
Процедура Solve имеет простую реализацию и может быть модифицирована для решения различных задач распознавания отрезков прямых:

if P[x,y]=0 then
	if AA[1,y,u]>PR then begin
		inc(nL); L[nL,1]:=x; L[nL,2]:= y;
		L[nL,3]:=u; L[nL,4]:=A[1,y,u];
	end;

Глобальный порог PR отсеивает отрезки меньшей длины. На рис. 19 показаны результаты компьютерного эксперимента A001 по сегментации дискретной области размером 34 × 28, с глобальным порогом PR = 19.


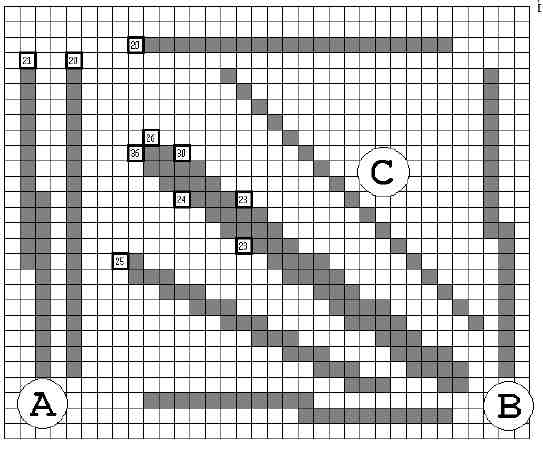
Рисунок 19 — Результат эксперимента A001.
На рис. 19 точка начала отрезка показана квадратной рамкой с числом. Число — это длина отрезка в виде количества итераций по алгоритму Брезенхейма. Линия А была обнаружена в отличие от линии B, потому что растровая модель прямой с на- клоном в 1 градус совпала с изображением отрезка. Линия С не может быть обнару- жена, так как не соответствует четырёхсвязной модели Брезенхейма. Всего алгоритм обнаружил 26 отрезков. При понижении глобального порога до 7 алгоритм A2 обнаружит 282 отрезка. Результат эксперимента A003 показан на рис. 20.
Все результаты тестирования работы алгоритмов проводились на компьютере Pentium IV 2,6 ГГц, ОЗУ 512 Мб, ОС Windows 2003 и приведены в табл. 1. Результаты экспериментов A010 и A011 показали одинаковую скорость работы алгоритмов, которая не зависит от количества подобранных моделей прямых линий.


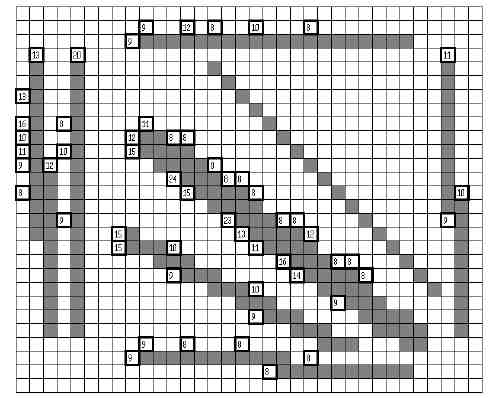
Рисунок 20 — Результат эксперимента A003.

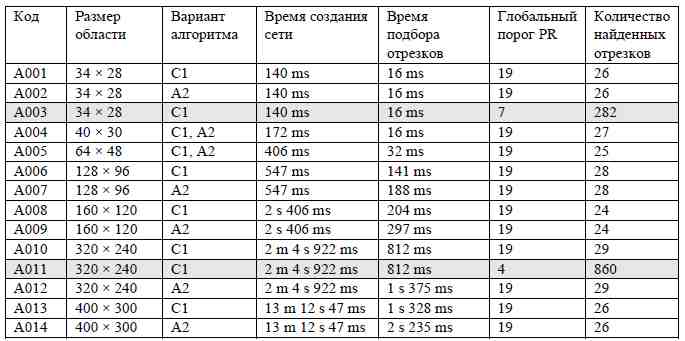
Таблица 1 — Результаты компьютерных экспериментов.
Выводы

Практическое открытие уникального алгоритма сегментации изображения SPІRAL качественно изменяет принципы организации вычислительного процесса распознавания роботом графических фигур, состоящих из прямых отрезков. В первую очередь, алгоритм реализуется аппаратно, а во вторую очередь, алгоритм выполняет анализ сцены любой сложности за фиксированное время, что важно в режиме реального времени робота.
Подбор прямой является процедурой первичной обработки данных в системах распознавания образов. Для пространства N = 640 на M = 480 ячеек, где N больше M и для U = 91 пучка прямых линий, алгоритму необходимо U*(2*M+N) ячеек памяти, что составляет 47,4% от ячеек, занимаемых самим пространством N*M. Разрабо- танный целочисленный алгоритм сегментации реализуется простым цифровым устройством на регистрах памяти, сумматорах и элементах задержки. Поэтому схему подбора отрезков прямой графической сетью можно адаптировать для использования в мобильных роботах.


Литература

1. Гудаев О.А. Сегментация аффинных проекций маркеров ARGET робототехнической системой / О.А. Гудаев // Искусственный интеллект. — 2007. — № 4. — С. 580-586.
2. TrendZoom является официальным представителем Ли Эделькорт и ее компаний (Trend Union, Studio Li Edelkoort) в Украине [Электронный ресурс]. — Режим доступа : www.trendzoom.com.ua/about.html
3. Гудаев О.А. Синтез и анализ предложений графического языка передачи сообщений в мобильных робототехнических системах с элементами расширенной реальности (ARGET) / О.А. Гудаев // Искусственный интеллект. — 2006. — № 2. — С.467-498.
4. Форсайт Дэвид А. Компьютерное зрение. Современный подход / Дэвид Форсайт, Жан. Понс ; [пер. с англ.]. — М. : Издательский дом «Вильямс», 2004. — 928 с.
5. Шапиро Л. Компьютерное зрение / Л. Шапиро, Дж. Стокман ; [пер. с англ.]. — М. : БИНОМ. Лаборатория знаний, 2006. — 752 с.
6. Гудаев О.А. Графический язык роботов ARGET / О.А. Гудаев // Системный анализ и информационные технологии : материалы XI Международной научно-технической конференции, (Киев, 26-30 мая 2009 г.). — К. : УНК «ИПСА» НТУУ «КПИ», 2009. — С. 291-291.
7. Гудаєв О.О. Організація зграєвої взаємодії в групах робототехнічних пристроїв з використанням графічної мови розширеної реальності ARGET / О.О. Гудаєв // Комп’ютерні науки та інженерія : матеріали III Міжнародної конференції молодих вчених CSE-2009, (Львів, 14-16 травня 2009 р.). — Львів : Видавництво Національного університету «Львівська політехніка», 2009. — С. 125-128.
8. Эгрон Ж. Синтез изображений. Базовые алгоритмы / Эгрон Ж. ; [пер. с фр.]. — М. : Радио и связь, 1993. — 216 с.
9. Фу К. Робототехника / Фу К., Гонсалес Р., Ли К. ; [пер. с англ.]. – М. : Мир, 1989. — 624 с.
10. Ефимов Н.В. Высшая геометрия / Ефимов Н.В. — [4-е изд.]. — М. : Гос. изд. физ.-мат. лит., 1961. — 580 с.
11. Аладьев В.З. Основы информатики : учебное пособие / Аладьев В.З., Хунт Ю.Я., Шишаков М.Л. — М. : Информационно-издательский дом «Филинъ», 1998. — 496 с.
12. Огнев И.В. Ассоциативные среды / И.В. Огнев, В.В. Борисов. — М. : Радио и связь, 2000. — 312 с.
13. Шикин А.В. Компьютерная графика. Полигональные модели / А.В. Шикин, А.В. Боресков. — М. : ДИАЛОГ-МИФИ, 2001. — 464 с.
14. Никулин Е.А. Компьютерная геометрия и алгоритмы машинной графики / Никулин Е.А. — СПб. : БХВ-Петербург, 2003. — 560 с.