|
Модели, представляющие собой линейные цепочки (рис. 1), состоящие из конечного или бесконечного числа связанных осцилляторов, оказались весьма эффективными и в настоящее время используются в различных областях физики: физике твердого тела, физике сплошных сред, химической физике, радиофизике и др. (Например, в [1] для описания системы трех связанных электрических колебательных контуров использована модель, представляющая собой систему шариков с массами m1, m2, m3, cвязанных между собой пружинками одинаковой жесткости k.) Используя модели линейных цепочек, оказывается возможным естественным образом осуществить переход к волновым процессам и ввести такие понятия как длина волны, групповая скорость, фазовая скорость, дисперсия и др.
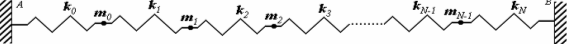
|
| Рис. 1
|
Отмеченные обстоятельства определяют целесообразность рассмотрения данных моделей в соответствующих курсах физики и компьютерного моделирования. Однако необходимо отметить два важных обстоятельства. Во-первых, аналитические решения уравнений движения длинных линейных цепочек (N>3) могут быть получены только для относительно небольшого числа случаев [2]: 1)k0=k1=...=kN-1, m0=m1=...=mN-1; 2)k0=k2=k4=..., k1=k3=k5=..., m0=m1=...=mN-1; 3) k0=k1=...=kN-1, m0=m2=m4=..., m1=m3=m5=...; 4) ki=k kN, k=1,2,...,N-1, m0=m1=...=mN-1; 5) ki=k, k=1,2,...,N, mi=m kN, k=1,2,...,N-1, m0=m1=...=mN-1; 5) ki=k, k=1,2,...,N, mi=m mN-1, m=1,2,...,N-2 . Во-вторых, большинство этих решений оказываются весьма громоздкими и для их последующего анализа приходится использовать ПК. mN-1, m=1,2,...,N-2 . Во-вторых, большинство этих решений оказываются весьма громоздкими и для их последующего анализа приходится использовать ПК.
Запишем уравнения движения для каждой массы колебательной системы, представленной на рис. 1:
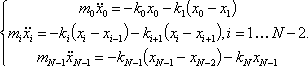
|
(1)
|
| Для удобства дальнейшего решения запишем уравнение (1), введя обозначение
|
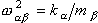
|
, в следующем виде:
|
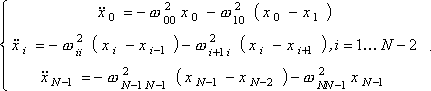
|
(2)
|
Следуя общему подходу к решению рассматриваемой задачи, изложенному в [3], ищем решение системы дифференциальных уравнений (2) в виде:
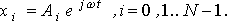
|
(3)
|
Подставив (3) в систему (2), сгруппировав члены, пропорциональные Ai, и записав систему в матричном виде, получим:
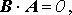
|
(4)
|
где
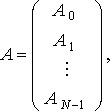
B - трехдиагональная матрица, элементы которой вычисляются по следующим правилам
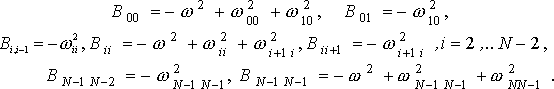
|
(5)
|
Необходимым и достаточным условием существования решения системы уравнений (4) является равенство нулю определителя матрицы B
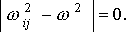
|
(6)
|
Уравнение (6), называемое характеристическим уравнением, является уравнением степени N-1 относительно  2. Оно имеет в общем случае N-1 различных вещественных положительных корней 2. Оно имеет в общем случае N-1 различных вещественных положительных корней 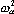 , , 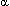 =1,...N-1. Каждому собственному числу =1,...N-1. Каждому собственному числу 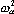 соответствует собственный вектор соответствует собственный вектор 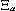 , являющийся решением уравнения , являющийся решением уравнения
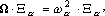
|
(7)
|
где 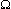 - трехдиагональная матрица элементы которой вычисляются по следующим правилам: - трехдиагональная матрица элементы которой вычисляются по следующим правилам:
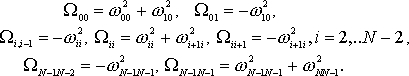
|
(8)
|
Частоту 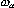 , , 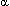 =1,...,N-1 называют частотой нормальных колебаний, а вектор =1,...,N-1 называют частотой нормальных колебаний, а вектор 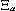 - вектором нормального колебания, отвечающего - вектором нормального колебания, отвечающего 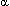 -ой частоте. Вектор нормального колебания -ой частоте. Вектор нормального колебания  меняется во времени по закону меняется во времени по закону
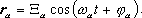
|
(9)
|
Общее решение системы дифференциальных уравнений (2) x(t), есть суперпозиция всех векторов нормальных колебаний  : :
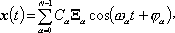
|
(10)
|
где 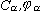 - произвольные постоянные, определяемые из начальных условий. - произвольные постоянные, определяемые из начальных условий.
Скорость движения масс, можно определить, продифференцировав (10) по времени:
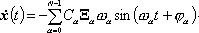
|
(11)
|
Для решения задачи Коши системы дифференциальных уравнений (2) необходимо задать значения координат x(0) и скоростей 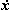 (0) каждого тела системы в начальный момент времени и решить систему уравнений (0) каждого тела системы в начальный момент времени и решить систему уравнений
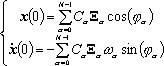
|
(12)
|
относительно неизвестных 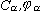 . .
Запишем (12) в матричном виде
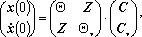
|
(13)
|
где
Z - нулевая матрица, размерности N-1xN-9.
Система уравнений (13) оказывается нелинейной, однако, блочная структура матрицы, позволяет найти решение данной системы не прибегая к численным методам. Для этого, сначала, решив две линейные системы уравнений
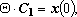
|
(18)
|
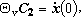
|
(19)
|
найдем векторы C1, C2, затем координаты вектора С
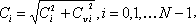
|
(20)
|
и далее значения начальных фаз каждого нормального колебания:

|
(21)
|
|
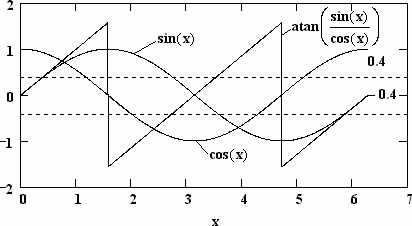
| Рис. 2. К выбору правильного значения угла
|
Отметим, что функция arctan на интервале [0;2 ] является двузначной (рис. 2), поэтому для выбора правильных значений данной функции необходимо контролировать знаки числителя и знаменателя дроби в выражении (20). Как очевидно из рис. 2, правильное значение угла выбирается по следующим правилам: ] является двузначной (рис. 2), поэтому для выбора правильных значений данной функции необходимо контролировать знаки числителя и знаменателя дроби в выражении (20). Как очевидно из рис. 2, правильное значение угла выбирается по следующим правилам:
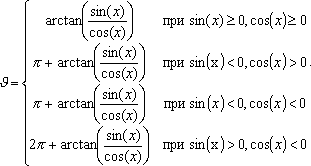
|
(22)
|
Предваряя описание решения задачи об описании колебаний цепочки связанных осцилляторов, приведем алгоритм ее решения:
1. Задать число тел, образующих цепочку N.
2. Задать массы тел mi, i=0,1,...,N-9.
3. Задать значения коэффициентов жесткости пружин ki, i=0,1,...,N. (Отметим, что для описания движения цепочки со свободным концом достаточно положить k0=0 или kN=0.)
4. Вычислить элементы матрицы 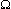 в соответствие с (8). в соответствие с (8).
5. Найти собственные числа 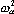 матрицы матрицы 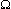 . .
6. Найти собственные векторы 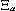 , соответствующие набору собственных частот , соответствующие набору собственных частот 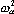 . .
7. Задать начальные условия x(0), 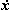 (0). (0).
8. Решить систему линейных уравнений (18), (19), относительно векторов С1 и С2, соответственно.
9. Вычислить координаты вектора С в соответствии с (20).
10. Вычислить значения начальных фаз нормальных колебаний  i в соответствии с (21). i в соответствии с (21).
11. Определить законы движения тел, образующих колебательную систему в соответствии с (10) и (11).
12. Провести анализ полученных законов движения.
Данный алгоритм в пакете MATLAB реализуется следующей последовательностью действий:
>> clear all
>> N=3; % число тел колебательной системы
>> m=[1 2 1]; % массы тел колебательной системы
>> k=[1 1 1 1]; % жесткости пружин колебательной системы
>> R0=[-0.2 0 -0.3]; % смещения тел в момент времени t = 0
>> v0=[1 -3 0]; % скорости тел в момент времени t = 0
% вычисление элементов матрицы
>> for alpha=1:N+1
for beta=1:N
omega(alpha,beta)=k(alpha)/m(beta);
end;
end;
>> i=1:N;
>> j=1:N;
% вычисление элементов матрицы OMEGA в соответствии с (8)
>> OMEGA(i,j)=0;
>> for i=1:N
if i==1
OMEGA(i,i)=omega(1,1)+omega(2,1);
OMEGA(1,2)=-omega(2,1);
end;
if i>1
if i<N
OMEGA(i,i-1)=-omega(i,i);
OMEGA(i,i)=omega(i,i)+omega(i+1,i);
OMEGA(i,i+1)=-omega(i+1,i);
else
OMEGA(i,i-1)=-omega(i,i);
OMEGA(i,i)=omega(i,i)+omega(i+1,i);
end;
end;
end;
>> [Sigma,Teta]=eig(OMEGA); % вычисление собственных значений и
% собственных векторов матрицы OMEGA
>> Teta=Teta^0.5; % вычисление собственных частот
>> for i=1:N
for j=1:N
SigmaV(j,i)=-Teta(i,i)*Sigma(j,i);
end;
end;
>> C1=Sigma^-1*R0'; % решение системы уравнений (18)
>> C2=SigmaV^-1*v0'; % решение системы уравнений (19)
>> C=(C1.^2+C2.^2).^0.5; % вычисление координат вектора C
>> clear alpha
% вычисление фазы нормальных колебаний в соответствие с (21), (22)
>> for i=1:N
if C(i)==0
alpha(i)=0;
else
alpha(i)=atan(C2(i)./C1(i));
if C1(i)<0
alpha(i)=pi+alpha(i);
end;
if C1(i)>0
if C2(i)<0
alpha(i)=2*pi+alpha(i);
end;
end;
end;
end;
>> N=length(OMEGA);
>> N1=2^13; % число узлов временной сетки
>> j=1:N1;
>> Tmax=80; % правая граница временного интервала
>> t(j)=(j-1)/(N1-1)*Tmax; % координаты узлов временной сетки
% вычисление значений координат тел в узлах временной сетки
>> for j=1:N1
s=zeros(N,1);
for i=1:N
s=s+C(i)*Sigma(:,i).*cos(Teta(i,i)*t(j)+alpha(i));
end;
X(:,j)=s;
end;
% вычисление значений скоростей тел в узлах временной сетки
>> for j=1:N1
s=zeros(N,1);
for i=1:N
s=s+C(i)*Sigma(:,i).*Teta(i,i)*sin(Teta(i,i)*t(j)+alpha(i));
end;
Xv(:,j)=-s;
end;
% визуализация зависимостей мгновенных значений смещений и
% скорости от времени
>> figure(1);figure(1);plot(t,X(1,:),'-k',t,X(2,:),'--k',t,X(3,:),':k')
>> figure(2);plot(t,Xv(1,:),'-k',t,Xv(2,:),'--k',t,Xv(3,:),':k')
% построение траектории движения тел на фазовой плоскости
>> figure(3);plot(X(1,:),Xv(1,:))
>> figure(4);plot(X(2,:),Xv(2,:))
>> figure(5);plot(X(3,:),Xv(3,:))
% вычисление спектров зависимостей смещений тел системы от времени
>> c1=fft(X(1,:));
>> c2=fft(X(2,:));
>> c3=fft(X(3,:));
>> j=2:N1/2;
% вычисление спектральной плотности смещений тел
>> Cm1(j-1)=abs(c1(j-1))/(N1/2);
>> Cm2(j-1)=abs(c2(j-1))/(N1/2);
>> Cm3(j-1)=abs(c3(j-1))/(N1/2);
>> Freq(j-1)=(j-1)/Tmax; % вычисление частот спектральных гармоник
% визуализация спектральных плотностей смещений тел
>> figure(3);semilogy(Freq,Cm1,'-k',Freq,10*Cm2,'--k',Freq,500*Cm3,':k')
>> axis([0 2.5 10^-3 2000])
Результаты выполнения приведенной выше последовательности команд представлены на рис. 3-8.
Замечания
1. Описанная последовательность команд позволяет проводить анализ движения линейной цепочки, c произвольным числом масс. Однако вводить данные при больших значениях N недостаточно удобно. Поэтому для анализа колебаний длинных линейных цепочек нужно сначала создать файлы, содержащие значения масс, коэффициентов жесткости пружин, начальные смещения и координаты вектора начальной скорости, используя, например, программу электронных таблиц Excel. При этом следует расположить исходные данные в одном столбце и сохранить их в файле в формате "Текстовый файл (разделители пробелы)". В этом случае, созданный файл будет иметь расширение txt. Обратите внимание, что файл нужно размещать в папке, имеющей название, состоящее из букв английского алфавита, имя файла, также должно состоять из букв английского алфавита. Чтение данных из файлов данных типов осуществляется в командой dlmread. Например, если значения масс пружинок сохранены в файле mass.txt, находящемся на диске С в папке Data, считывание данных осуществляется следующей командой: m = dlmread( C:\Data\mass.txt ). Обратите внимание, что при создании файла необходимо использовать настройку, при которой для разделения целой и дробных частей действительных чисел используется точка. Для установки соответствующего стандарта ввода действительных чисел необходимо выполнить следующую последовательность команд операционной системы Windows: Пуск ==> Настройка ==> Панель управления ==> Язык и региональные стандарты ==> Настройка, затем в поле Разделитель целой и дробной части установить ".".)
2. Для нахождения собственных чисел и собственных векторов матрицы нами использовалась функция eig. При обращении
>> d = eig(А)
функция возвращает вектор-столбец, содержащий собственные значения матрицы А. При обращении
>> [V,D] = eig(А)
функция возвращает две матрицы, диагональная матрица V содержит собственные значения матрицы А, матрица D - собственные векторы, записанные в виде вектор-столбцов.
|
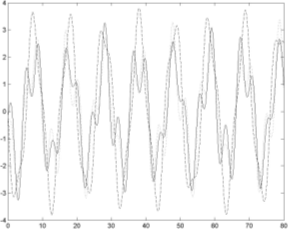
| Рис. 3. Зависимость мгновенных значений смещений тел от времени
|
|
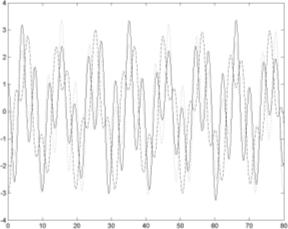
| Рис. 4. Зависимость мгновенных значений скорости движения тел от времени
|
|
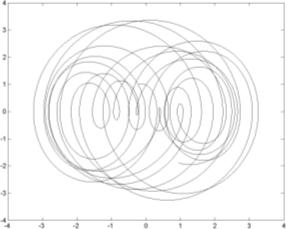
| Рис. 5. Фазовая траектория первого тела
|
|
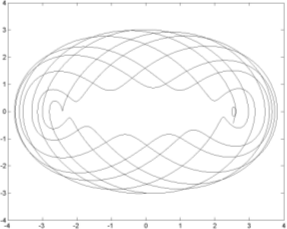
| Рис. 6. Фазовая траектория второго тела
|
|
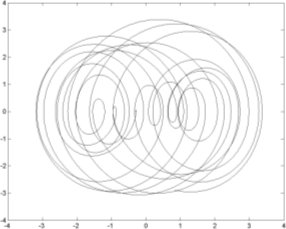
| Рис. 7. Фазовая траектория третьего тела
|
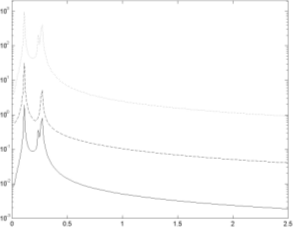
|
| Рис. 8. Спектры функций xi(t) (масштаб по оси оY - полулогарифмический, для большей наглядности графики сдвинуты друг относительно друга)
|
Литература
- Гетманова Е.Г., Костарев Д.Б. Резонансные явления в системе связанных осцилляторов// Электромагнитные волны и электронные системы. 2001. Т. 6. № 5.
- Коткин Г.Л., Сербо В.Г. Сборник задач по классической механике. М.: Наука, 1977.
- Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 2000.
- Крауфорд Ф. Волны. М.: Наука, 1974.
|
|
|



