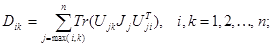Назад
в библиотеку
Разработка
алгоритма управления электромеханическим манипулятором на основе его
математической модели.
Авторы:
К.С. Перевозчиков, С.В. Павлов, магистранты; Г.С. Чекавский, доцент,
к.т.н
Источник: Вісник кафедри Електротехніка
за підсумками наукової діяльності студентів. – Донецьк, ДонНТУ,
2012 – c.68-69.
Аннотация
Перевозчиков
К.С., Павлов С.В., магістранти; Чекавський Г.С., доц., к.т.н. Розробка
алгоритму керування електромеханічним маніпулятором на основі його
математичної моделі.
Наведено загальні відомості про електромеханічні маніпулятори,
зазначено критерії якості їхнього функціонування, окреслені особливості
маніпуляторів. Описано задачу розробки математичної моделі
маніпулятора. Зазначені відомості планується застосовувати при розробці
математичної моделі маніпулятора MANUS.
Рассматривается
электромеханический манипулятор – устройство, в общем случае
состоящее из нескольких кинематически связанных звеньев, обеспечивающих
движение с несколькими степенями свободы, предназначенное для
выполнения определенных перемещений исполнительного органа (ИО) в
соответствии с заранее заданной программой. Каждое отдельное звено
электромеханического манипулятора приводится в движение от
индивидуального электропривода. В последнее время формирование сигналов
задания на движение отдельных звеньев выполняется без непосредственного
влияния человека – так называемые роботы-манипуляторы
(автоматические манипуляторы). С точки зрения условий применения и
возлагаемых задач следует выделить промышленные (общего применения) и
специальные манипуляторы.
Расширенное управление
роботом-манипулятором предполагает достижение всех или некоторых из
ниже перечисленных свойств и критериев[1]
:
- абсолютная жёсткость звеньев
манипулятора;
- требуемая грузоподъёмность и
производительность;
- заданное качество переходных
процессов (быстродействие, динамика);
- точное управление моментом
каждого звена;
- точное управление положением
и/или скоростью ИО;
- возможность управления
силой, развиваемой ИО;
- надлежащая чувствительность
и простота управления манипулятором;
- достаточная вычислительная
мощность для обработки требуемых в зависимости от применения алгоритмов
управления в режиме реального времени.
Однако на практике
манипуляторы, которые обеспечивают в полной мере все из перечисленных
характеристик, отсутствуют.
В промышленных роботах общего
применения для каждой из перечисленных характеристик задается своя
требуемая точность достижения критериев, перечисленных выше.
Специальные манипуляторы, например, предназначенные для обслуживания
людей с ограниченными способностями, имеют характеристики, по своим
показателям практически на порядок и более превосходящие характеристики
промышленных. Это обусловливает и применение существенно более сложных
алгоритмов управления. Разработка таких манипуляторов и алгоритмов
управления ими актуальны с точки зрения как научного, так и социального
значения.
В лаборатории кафедры
«Электропривод и автоматизация промышленных
установок» имеется манипулятор MANUS (рис.1), обладающий
сложной кинематикой (7 степеней свободы), предназначенный для помощи
людям с ограниченными возможностями опорно-двигательного аппарата.

Рисунок
1 – Манипулятор MANUS
Основной особенностью
электромеханических манипуляторов является использование редукторов,
использование которых обусловлено ограниченностью перегрузочной
способности большинства электрических машин. С другой стороны, это
позволяет разработчику манипулятора использовать машины с меньшими
габаритами. В общем случае, редукторы привносят следующие задачи,
влияющие на сложность алгоритма управления:
- трение в кинематических
передачах;
- необходимость учёта конечной
жёсткости звеньев манипулятора;
- ограничения, налагаемые на
величину частот вращения электрических машин;
- преобладание динамической
составляющей в моменте, развиваемом двигателями манипулятора.
Синтез алгоритма управления
манипулятором наиболее целесообразно выполнить на основе
математического описания процессов в нем. Однако, в зависимости от
исследуемых показателей, применяется несколько видов математических
моделей.
С точки зрения геометрии и
кинематики манипуляторов в настоящее время используется преобразование
Дэнавита-Хартенберга (Denavit-Hartenberg frame assignment). Уравнения
прямой кинематики определяют связь между декартовыми положениями и
углами и пространством положений звеньев манипулятора и его ИО.
В наиболее общем виде
манипулятор со звеньями q1, …, qn (n – число
звеньев) характеризуется матрицей:
где
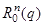 –
матрица
угловых положений,
–
матрица
угловых положений,
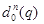 – матрица положения ИО.
– матрица положения ИО.
Стандартный метод получения
уравнений динамики основан на использовании так называемых уравнений
Эйлера-Лагранжа.
В наиболее общем виде,
манипулятор, имеющий n степеней свободы,
описывается уравнением в матричной форме[2]:
где
τ(t) – вектор
(размерностью n x 1) обобщённых сил,
создаваемых
силовыми приводами в звеньях манипулятора;
q(t) – вектор (размерностью n x 1) присоединённых переменных
манипулятора;
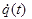 – вектор обобщённых
скоростей;
– вектор обобщённых
скоростей;
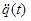 – вектор обобщённых
ускорений;
– вектор обобщённых
ускорений;
D(t) – симметрическая матрица размерностью nn, элементы
которой определяются выражением:
где
h(q) – вектор кориолисовых и центробежных сил;
c(q) – вектор гравитационных сил.
В настоящее время на основе
указанных положений ведется разработка математической модели
манипулятор MANUS для исследования различных алгоритмов управления
манипуляторами подобного назначения.
Список использованной
литературы
1. Sciavicco, L., Siciliano, B., “Modeling and Control of
Robot Manipulators” – London, Springer, 2000.
2. Фу К., Гонсалес Р., Ли К. Робототехника: Пер. с англ. –
М.: Мир, 1989. – 624 с.

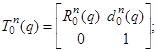
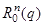 –
матрица
угловых положений,
–
матрица
угловых положений,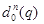 – матрица положения ИО.
– матрица положения ИО.
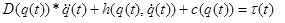
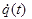 – вектор обобщённых
скоростей;
– вектор обобщённых
скоростей;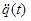 – вектор обобщённых
ускорений;
– вектор обобщённых
ускорений;