I.A. Sniegina, V.N. Khomenko, A.A. Melnyk
CONTROL OF COMPLIANT ELECTROMECHANICAL ROBOTS
WITH COMPLEXE KINEMATICS and OSCILLATORY OCCURRENCES IN JOINTS
Ó äàí³é ñòàòò³ ðîçãëÿäàºòüñÿ ñèñòåìà
óïðàâë³ííÿ ïoäàòëèâ³ñòþ ñóñòàâ³â åëåêòðîìåõàí³÷íîãî
ðîáîòà.
Introduction. Development of robotic technologies is
on a high level nowdays. Robots are used in
industrial plants, replacing persons completely or partially. They execute
technical operations of different complexity. Next, they help people in house
holding too. Notably robots interact more and more with peoples. The study of
interaction process between human and robot does not limited only with
technical aspects but fundamentals biologics paradigms are also applied [1].
This paper considers
control of compliant joints of a robot-manipulator. This compliance is due to
the reducer with deformable dentures “Harmonic Drive”. The robot joints are
initially controlled with a classical PID controller.
PID controller. A proportional–integral–derivative controller (or, simply PID) is a generic control loop feedback mechanism widely used in industrial control systems – a PID is the most commonly used feedback controller. It calculates an "error" value as the difference between a measured process variable and a desired setpoint, its derivate and integral. The controller attempts to minimize the error by adjusting the process control inputs [3].
The PID control scheme is named
after its three correcting terms, whose sum constitutes the manipulated
variable. The proportional, integral, and derivative terms are summed at the
output of the PID controller. Defining u(t) as
the controller output, the final form of the PID algorithm is:
where
Kp - proportional gain, a tuning
parameter; Ki - integral gain, a tuning parameter; Kd - derivative gain, a tuning parameter;
e - error = SP – PV; t - time or instantaneous
time (the present).
In this article we use
a simple proportional controller to accentuate the influence of the reducer
nonlinearities on the dynamics of the whole system.
Analysis
of paper H. Serhan, C. G. Nasr, P. Henaff – Muscle emulation with DC motor and neural networks
for biped robots [5]. Present paper show that it’s possible to model
a nonlinear muscle model using a robot joint entrained with a DC motor
controlled by a PID controller . The DC motor and PID
are couples in a closed loop. The controller is tuned by Neural Network. Neural
Network is a Multi-Layer-Perceptron. Tuning the PID of each of the DC-Motors
implemented in articulations of the robot permit to obtain dynamic of movement
equivalent to a human dynamics. The modeling implemented for the knees of a
biped robot but the compliance effect of reducer does not taken into account
and the robot is considered entirely rigid.
But the proposed by P. Henaff et al. [5] approach
open dors to a world of biologically insipid control
of robots. This is a new field on robotic control and shoud
be studied in more details.
Bioinspiration. The past years science and technology
developed under profound influence of the computer technology. Failures because
of these technologies usage enforce to recover fundamentals of biologics
paradigms. More exactly, biological approach permits to achieve «naturals»
interaction of robots with humans and their environment.
Particularly it is important by physique
interaction of robot with a human.
One of the
vertebrate locomotion model is based on the concept of
self-organized generators – Central Pattern Generators (CPG). This one can
found in articles Bassler, 1993 ;
Kollins, Ritchmond,
1994 ; Krous, 2002 ; Viller,
Miranker, 1993. There is exists a problem of creation
robot, which will act similar to a human. Advantages of utilizing CPG in
robotics can be found in works of Ijspeert, 2008, Batchli, 2006, Matsuoka, 1995 [2].
Oscillator of Rowat-Selverston.
Biological neurons with several canals have
complicated structure that creates difficulties in their modeling. American
scientists Rowat and Selverston
have presented (in 1997) an approximated model of such neuron. They took into
account two groups of currents (“slow” and “fast”) and proposed two first order
differential equations connecting currents and tensions. The fast current is
described by equation (1) and the slow – by equation (2):
,
(2)
where 
, 
- neuron membrane time
constant; 
- time constant of a slow
activation of currents; 
- injected current; U - membrane tension; q
- slow current; U and q - variables; F( U, σf ) - nonlinear voltage-current characteristic of the fast current [5].
Christian Ott, Alin Albu-Schaffer, Andreas Kugi – A passivity based cartesian
impedance controller for flexible joint robots. [6] In this paper it has
been exhibit that the feedback of joint torques for a flexible joint robot can
be presented physically as a scaling of a motor inertia. This allows the
combination of a torque feedback action with any controller designed for
flexible joint robots. Christian Ott treated in
detail the case of a Cartesian impedance controller.
Christian Ott is the most famous scientist working on
problems of interaction between the robot and the environment. In his works he
took into account elastic comportment of the robot joints.
It
may be noted that he did not published works on the interaction of a
«handshake» type with a human.
Mathematical
model of a Harmonic Drive reducer. Reducer is a principal matter of mechanical compliance
in joints of humanoids robots having rigid structure. Particularly this is a
Harmonic Drive reducer (fig. 1). It consists of three parts. There are: wave generator, flexspline
and circular spline. The elasticity arises in flexspline.
Harmonic Drive
can exhibit much more complex dynamic behavior than gear transmissions without flexispline (epicyclic or
worm-and-wheel gearbox) [7] but it has a zero backlash.
Figure 1 – Harmonic
Drive components [7]
The reducer exhibits also
significant friction in flexispline and in bearing.
The equation of friction [7]:
where
Tfm - friction torque; Tvn
- viscous torque for negative direction of angular velocity; Tvp -
viscous torque for positive direction of angular velocity; Tsn
- Coulomb friction negative direction of angular velocity; Tsp - Coulomb friction
positive direction of angular velocity; u-1(x) - special
function [7].
The compliance model it presented by
the next equation [7]:
where Tmeas
- measurable torque of motor; Δθ - flexspline relative torsion.
Simulation procedure. Modeling is executed in the
Simulink MATLAB eviroment. The model containing joint
driving motor (fig. 2a) and a Harmonic Drive reducer
(fig.
2b) was created. The load of a joint was modeled as a constant reactive
opposite torque.
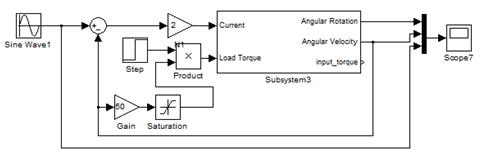
a)
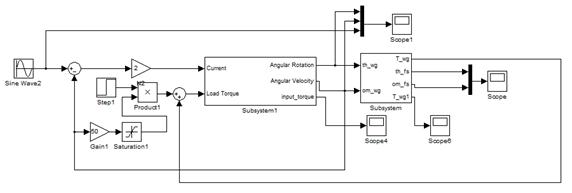
b)
Figure 2 - Simulation of a motor (a)
and full system with Harmonic Drive reducer and proportional regulator (b)
Analysis of simulation results.
The real angular
velocity differs from the desired velocity, because there is a load, which
gives a static error (the curve shape of angular velocity and angular position
are slightly different one from another (fig. 3, a) as a proportional regulator
is used. The effect becomes more important when the model of Harmonic Drive
reducer is added. The considered regulator does not able to overcome the effect
of nonlinearities of the reducer (fig. 3, b).
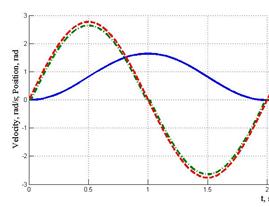
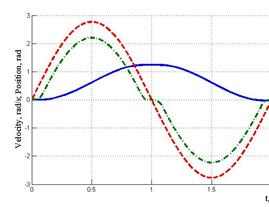
a)
b)
Figure 3 - Simulation results: a)
motor; b) motor-HD
As one can see on the figure 3b, the static error becames much more important because of compliant behavior
and Coulomb friction in the HD reducer. Also, stiction
influences at low speed. The total positioning error exceeds 10%. The problem
should be solved with more sophisticated regulators.
Resume. This article describes links internal dynamics of elastic robots with
complex kinematics. Taking into account internal elasticity of joints is
important. It influence on the interaction quality of a robot with its
environment, especially when interacting with human. The one can sense this phenomena when a classical PID regulation approach is
employed. In the considered type of robots elasticity arises mainly from
the robot Harmonic Drive reducer. We show this effect in simulations. A
special, biologically inspired approach is needed to control interaction with a
human in a natural, more perceptive way. Thus, we investigate to employ Rowat-Selverston neural oscillator to control vibration
phenomena in joints of an interacting robot.
Bibliography
1. E. Gelenbe. Biologically inspired operations research //
European Journal of Operational Research 108 (1998) 239 – 240.
2. T. Zielinska. Biological inspiration used for robots motion
synthesis // Journal of Physiology – Paris, 103 (2009) 133 – 140.
3.
http://en.wikipedia.org/wiki/PID_controller.
4. H. Serhan, C. G. Nasr, P. Henaff. Muscle emulation with DC
motor and neural
networks for biped robots
// International Journal of Neural Systems. – 12 c.
5. E. Snegina, A. Pougatch,V. Khomenko, A. Melnyk, P. Henaff, V. Borysenko.
Practical aspects of Rowat-Selverston bio-inspired oscillator simulation // Íàóêîâ³ ïðàö³ Äîíåöüêîãî
íàö³îíàëüíîãî òåõí³÷íîãî óí³âåðñèòåòó 11 (186), 2011. – 369 - 373.
6. C. Ott, A. Albu-Schaffer, A. Kugi, S. Stramigioli, G. Hirzinger. A passivity based cartesian impedance
controller for flexible joint robots – Part 1: Torque feedback and gravity
compensation. – 7 c.
7. H.D. Taghirad, P.R. Bélanger.
Modeling and parameter identification of Harmonic Drive systems // Journal of
Dynamic Systems, Measurements, and Control. – 22 c.