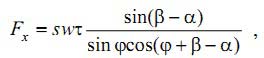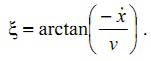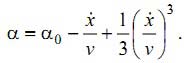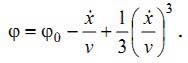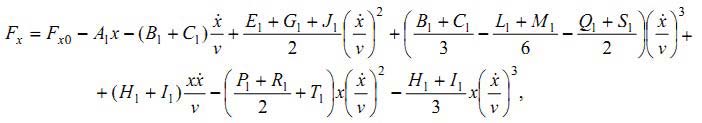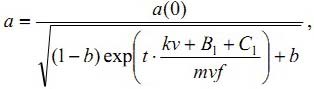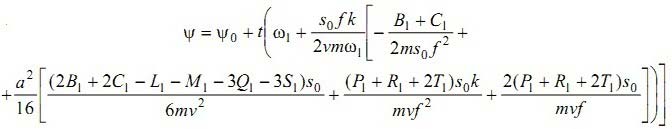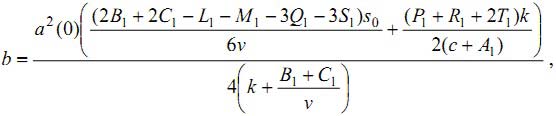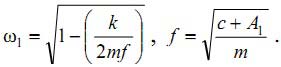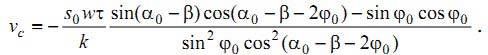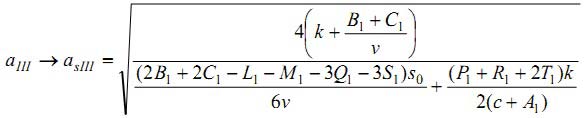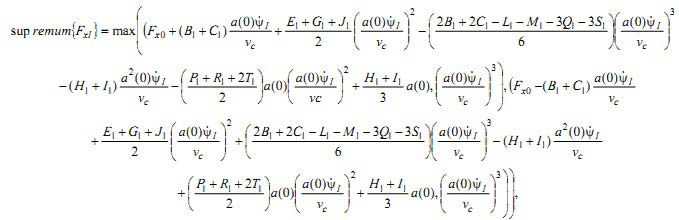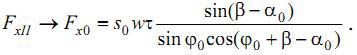Аннотация.
В этой статье исследован вид автоколебаний при резании металла. Модель системы основана на прогнозирующей теории модели зоны резания. Так как динамическая сила резания в значительной степени определяется режимами резания при вибрациях, цель данной статьи рассмотреть изменения переднего угла и угла сдвига при варьировании значением подачи, а также предложить модифицированную нелинейную модель изменения силы резания и, следовательно, нелинейную аналитическую модель вибраций. Путем анализирования аналитических решений были обнаружены три вида колебательного движения. Для каждого из них численно выражены изменения компонента силы резания (осевой силы) и переднего угла, как функций времени.
Ключевые слова:
Резание металла, автоколебания.
1. Введение
Автоколебания при резании относятся к классу самовозбуждающихся вибраций, присутствие которых при обработке металла оказывает негативное влияние на качество поверхности и размерную точность обрабатываемой детали, на стойкость резца и даже на долговечность станка. Значительное число исследований посвящено исследованию различных механизмов и характеристик дрожания. Процесс резания с переменной подачей является одной из основных причин появления автоколебаний. Это обуславливает переменность силы резания. Пути решения этой проблемы могут быть практические и теоретические. Теоретические пути обычно выводятся из модели зоны резания и образования стружки [1,2] при условии постоянства параметров резания. Однако, эта особенность противоречит теоретическим и экспериментальным данным [3-6], согласно которым при резании некоторые параметры изменяются и, следовательно, переменна и сила резания. Тобиас и Фишвик [7] вывели первое аналитическое выражение изменения динамической силы резания как функцию от нарастающего изменения толщины стружки и величины подачи. Кейнт [3] усовершенствовал теорию стационарного ортогонального точения, учитывая влияние как толщины стружки, так и переднего угла. Нигм положил изменение параметров точения: подачи, переднего угла и скорости резания в основу размерного анализа [5,6]. Лиин и Вэнг [8] представляли силу резания зависящей от изменений угла сдвига. Из-за фундаментальных свойств процесса необходима нелинейная аналитическая модель [8]. Изучаются два аспекта нелинейности силы резания. Один из них – описание нелинейной силы резания зависящей от изменения толщины стружки высшего порядка [8,10-13], что подтверждает экспериментально установленное конечное значение амплитуды колебаний. Вторая заключается в рассмотрении разнообразных восстанавливающих эффектов [14,15].
Несмотря на большое количество теоретических исследований, обобщенная аналитическая модель вибраций пока месть не была создана, по причине сложности феноменологических процессов при резании. По этой причине крайне важно фундаментально исследовать механику осцилляторного резания.
В настоящей статье модель, базирующаяся на идее идеального разделения, модифицирована принятием в расчет угловых вибраций в плоскости, как зависящих от изменения параметров резания: подачи, переднего угла и угла сдвига. Также в модели учтена нелинейность процесса резания.
2. Моделирование осевой силы
Давайте рассмотрим процесс срезания ортогональных волн с образованием стружки по модели разделения на зоны. Для упрощения изложения, система представляется имеющей одну степень свободы (перемещение вдоль оси Х) (Рис. 1). Мерчант [1] вывел зависимость составляющей силы резания (осевой силы) Fx как функцию от условий резания, углов инструмента и условий трения между инструментом и заготовкой, то есть:
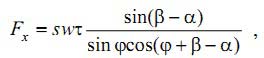 |
(1) |
где: s – подача; w – ширина резания; τ – напряжения сдвига; β – угол трения; α – передний угол; φ – угол сдвига.
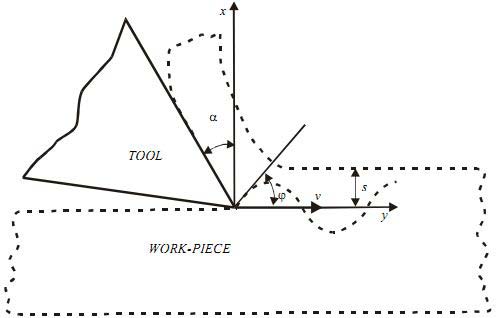
Рисунок 1. Схема ортогонального процесса резания с образованием сливной стружки
При осцилляторном точении предполагается появление процесса изменения подачи, переднего угла и угла сдвига с учетом их номинальных значений. Обозначим эти номинальные значения индексом 0. Таким образом, согласно с рис. 1, мгновенное значение подачи изменяется небольшим приращением, которое зависит от относительного движения инструмента вдоль оси Х, и принимает форму:
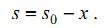 |
(2) |
Рисунок 2 иллюстрирует изменение переднего угла α. Легко увидеть, что изменение этого параметра эквивалентно малому углу ξ, который может быть выражен как функция от скорости резания V и интенсивности вибраций инструмента x:
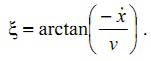 |
(3) |
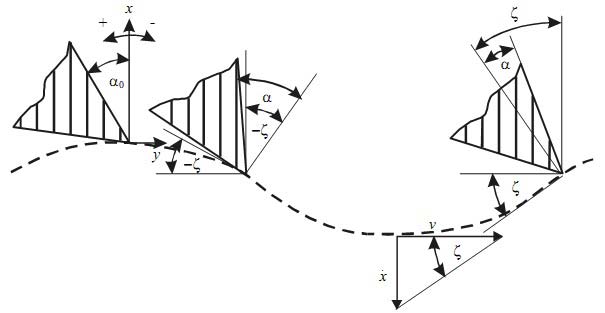
Рисунок 2. Изменение переднего угла при осцилляторном точении
Мгновенное значение переднего угла может быть найдено через нелинейное выражение угла ξ третьего порядка:
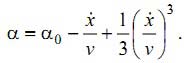 |
(4) |
В случае точения по следу, подобное изменение переднего угла приведет к пропорциональному изменению угла сдвига [6]. Для рассматриваемой системы это изменение обозначено как ξ, и мы получаем зависимость для определения мгновенного значения переднего угла:
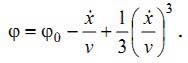 |
(5) |
Напряжение сдвига τ незначительно зависит от скорости резания [5] и может быть представлено как постоянная величина. Мгновенное значение осевой силы Fx может быть выражено с помощью использования разложения в ряд Тейлора до члена третьего порядка в окрестности номинальных значений (s0, α0, φ0) с учетом инкрементных геометрических изменений. Эти изменения определены разницами между мгновенными значениями следующих параметров: подачи, переднего угла, угла сдвига и их номинальными значениями. Таким образом:
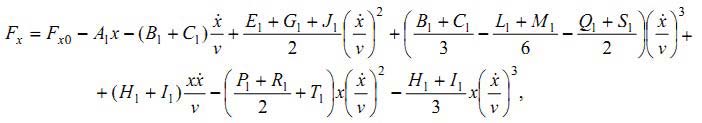 |
(6) |
коэффициенты этого выражения приведены в приложении.
3. Моделирование вибраций инструмента
Уравнение движения инструмента может быть записано в виде:
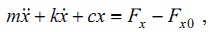 |
(7) |
где m – приведенная масса системы, 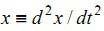 , t – время, k – эквивалентное затухание системы,
, t – время, k – эквивалентное затухание системы, 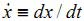 , c – приведенная жесткость системы,
Fx – приведено в уравнении (6), и Fx0 – номинальное значение осевой силы.
, c – приведенная жесткость системы,
Fx – приведено в уравнении (6), и Fx0 – номинальное значение осевой силы.
3.1. Движения инструмента
В соответствии со статьей [16] решение в первом приближении нелинейного полного дифференциального уравнения (7), представляет собой
где а – амплитуда вибраций, а(0) – начальная амплитуда,
ψ – фаза вибраций, ψ(0) – начальная фаза,
Из анализа этого уравнения устанавливается существование трех случаев движения. Когда член, сформированный коэффициентами демпфирования выражения движения (7), равен нулю, имеют место собственные колебания инструмента. Это условие выражает, так называемое, критическое значение силы резания:
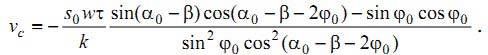 |
(11) |
Этому значению скорости резания соответствует предельное значение вибрации. Из выражения (9) можно сделать вывод, что амплитуда этого движения aI стремится к исходному значению:
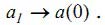 |
(12) |
Второй случай имеет место при резании со скоростью vII , которая больше критического значения, то есть для:
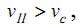 |
(13) |
имеет место затухающее колебательное движение. Амплитуда этого движения обращается в ноль:
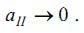 |
(14) |
Наконец, для системы резания со скоростью vIII , меньшей критической скорости:
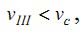 |
(15) |
имеют место самовозбуждающиеся вибрации. Амплитуда в этом случае aIII принимает значение установившееся значение для этого случая asIII:
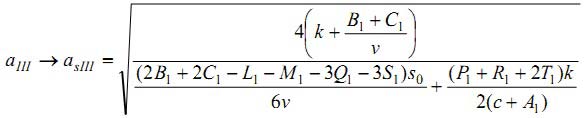 |
(16) |
В зависимости от начальной амплитуды, существует два возможных варианта поведения системы. Когда начальная амплитуда a(0) меньше установившегося значения asIII , амплитуда сначала возрастает, а затем принимает постоянное значение. Когда начальная амплитуда больше установившегося значения, амплитуда вначале убывает, а после достигает того же постоянного значения asIII.
Применяя численный метод второго порядка Рунге-Кутта к выражению (6) можно подтвердить наличие всех аналитически полученных случаев движения. Результат этой процедуры показан на рис. 3. В данной статье исследованы динамические характеристики по условиям испытаний, приведенным в таблице 1.
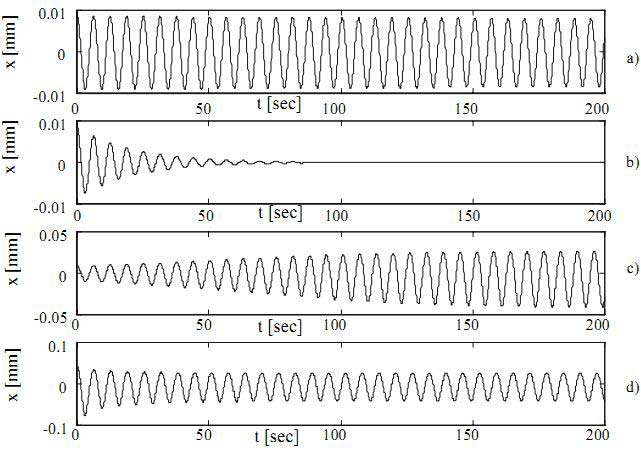
Рисунок 3. Колебательное движение инструмента: а) собственные колебания; b) затухающие колебания; c) автоколебания при a(0) < asIII ; d) автоколебания при a(0) > asIII.
| Приведенная масса системы |
m = 15 kg |
Напряжения сдвига |
τ = 655×106 Nm-2 |
| Приведенное затухание системы |
k = 400kg s-1 |
Угол трения |
β = 70o |
| Приведенная жесткость системы |
c = 3×106 Nm-2 |
Передний угол |
α0 = 10o |
| Подача (номинальное значение) |
s0 = 0.17 mm |
Угол сдвига |
φ0 = 10o |
| Ширина резания |
w = 2.5 mm |
|
|
| СЛУЧАЙ 1 |
|
a(0) = 0.0085 mm |
|
| СЛУЧАЙ 2 |
|
a(0) = 0.0085 mm |
|
| СЛУЧАЙ 3 |
a(0) < aSIII |
a(0) = 0.0085 mm |
|
| |
a(0) < aSIII |
a(0) = 0.034 mm |
|
3.2. Изменение осевой составляющей силы резания Fx
Особый интерес представляет изучение изменения осевой составляющей силы резания Fx во времени для вышеупомянутых случаев. А именно, когда динамическая сила резания побуждает структуру режущего инструмента генерировать вибрации, и как следствие этих колебаний, динамическая сила резания находится в циклическом влиянии. Другими словами, вибрации инструмента и динамическая сила резания формируют хорошо известную систему с обратной связью [12,17].
Для этого исследования был применен численный метод второго порядка Рунге-Кутта. Результаты процедуры применения этого метода к выражениям (7), (6) описаны на рис. 4.
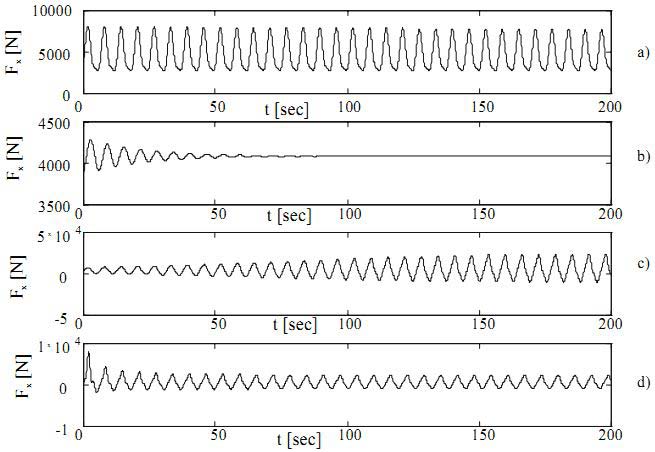
Рисунок 4. График изменения осевой силы по времени:
а) для случая собственных колебаний; b) для случая затухающих колебаний; c) для случая автоколебаний при a(0) < asIII ; d) для случая автоколебаний при a(0) > asIII .
Эффект и последствие свободных колебаний инструмента – гармоническое изменение значения осевой силы с постоянной амплитудой. Таким образом, согласно аналитическим решениям (8), (12) и выражению (6) мы получим:
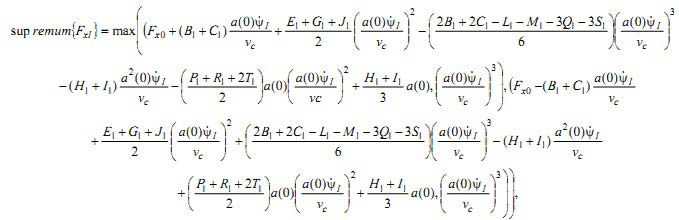 |
(17) |
где 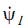 определено выражениями (10)-(12).
определено выражениями (10)-(12).
Случай с затухающими колебаниями, где амплитуда aII принимает нулевое значение и в значительной степени зависит от осевой силы FxII , которая при t > ∞ принимает то же значение, что и статическая сила упругости Fx0, то есть:
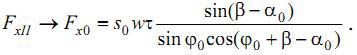 |
(18) |
Из рис. 4 и рис. 3 также можно заключить, что самовозбуждающиеся колебания осевой силы вызывает подобное движение инструмента. При t > ∞, осевая сила FxIII стремится к постоянной величине, которая не равна номинальному значению Fx0 :
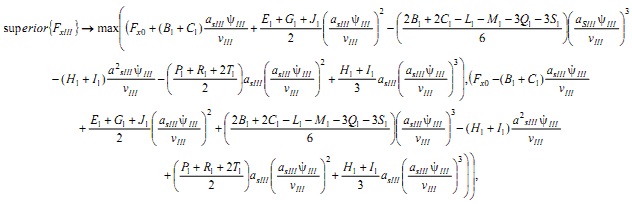 |
(19) |
где 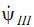 определяется исходя из уравнений (10), (15), (16).
определяется исходя из уравнений (10), (15), (16).
Линеаризированная модель осевой силы включалась в модель автоколебаний во многих исследованиях. Однако недостаток этих рассуждений в том, что линеаризированная модель не соответствует реальному процессу. То есть, результаты, полученные по линеаризированной модели, показывают, что осевая сила возрастает безгранично. Этот вывод подтверждается на рис. 5, сравнением результатов линеаризированной и нелинейной моделей осевой силы для условий, приведенных уравнением (15), и при a(0) < asIII .
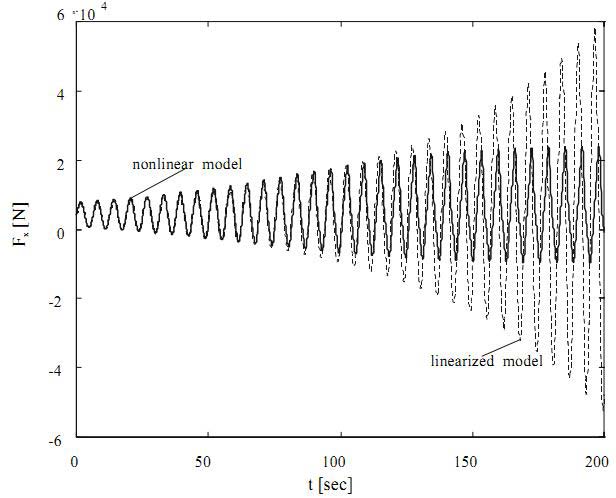
Рисунок 5. Сопоставление величин осевой силы: линеаризированной модели (штриховая линия), нелинейной модели (сплошная линия)
3.3. Изменения переднего угла
При изучении точения как динамического процесса, обычно берется во внимание изменение угла сдвига. Но зачастую пренебрегают изменением переднего угла, принимая его равным постоянной величине α0. Проанализируем точность этого упрощения. Исследование будет проводиться заменой численно полученного решения уравнения (7) на решение уравнения (4). На основании сравнения мгновенного значения переднего угла с его номинальным значением α0 можно обнаружить относительную погрешность, которая нанесена на рис. 6. Для случая свободного колебательного движения инструмента, передний угол αI изменяется в пределах от минимального значения αImin до максимального αImax. Для наших условий эксперимента, когда α0 = 100, область определения изменения переднего угла αII стремится к значению α0. Тем не менее, в начале процесса точения с колебаниями разница составляет около 2%. Если в системе присутствуют автоколебания, передний угол αIII имеет область определения, которая определена минимальным αIIImin и максимальным αIIImax значениями. Когда a(0) < asIII , αIIImin ≈ -16.30 и αIIImax ≈ 36.650; при a(0) > asIII , αIIImin ≈ -25.850 и αIIImax ≈ 48.490.
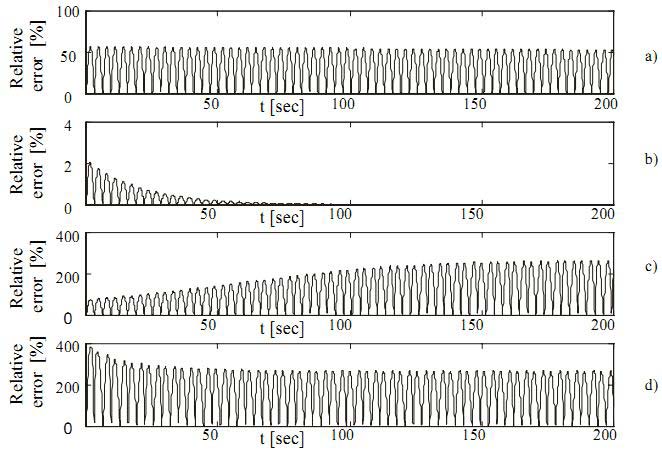
Рисунок 6. Относительная погрешность значений переднего угла как функции от времени: a) для случая свободных колебаний; b) для случая затухающих колебаний; c) для случая автоколебаний при a(0) < asIII; d) для случая автоколебаний при a(0) > asIII;
Из рисунка 6 видно, что для этого случая разница значительна, и ею нельзя пренебречь.
4. Заключение
Можно сделать следующие выводы:
– на движение инструмента оказывают решающее воздействие параметры резания. В зависимости от значения скорости резания с учетом ее критического значения, определенного в выражении (11) могут возникать следующие случаи:
- для процесса резания с критическим значением скорости резания (предельные колебаний) вибрации инструмента имеют постоянную амплитуду;
- когда скорость резания превышает критическое значение, колебательное движение инструмента исчезают и только при этом условии правомерна теория устойчивого резания;
- когда скорость резания меньше критического значения, возникают автоколебания.
Все эти выводы полностью согласуются с предшествующими экспериментальными и теоретическими результатами, которые определяли амплитуду вибраций не растущей безгранично, а стабилизирующейся на конечном значении.
– представленными нелинейной моделью вибраций и нелинейной моделью осевой силы, в которой учтены изменение подачи, переднего угла и угла сдвига, доказывается представление о системе вибрационного точения как о системе с обратной связью;
– существует значительное влияние наличия вибраций на изменение переднего угла для случаев свободных и автоколебаний, и по причине этого его постепенно нарастающее изменение должно быть учтено в будущих исследованиях.
Благодарность – Автор хотел бы выразить благодарность профессору L.J. Cveticanin за помощь при выполнении проекта.
Список использованной литературы
- M.E. Merchant, Mechanics of the metal cutting process: orthogonal cutting and a type 2 chip, J. Appl. Phys., Trans. ASME, vol. 16, pp. 267-275, 1945.
- M.E. Merchant, Mechanics of the metal cutting process: plasticity conditions in orthogonal cutting, J. Appl. Phys., Trans. ASME, vol. 16, pp. 318-324, 1945.
- G.S. Kainth, Investigation into the dynamic of the metal cutting process, Ph. D. dissertation, University of Birmingham, United Kingdom, 1969.
- W.A. Knight, Chatter in turning: some effects of tool geometry and cutting conditions, Int. J. Mach. Tool Des. Res., vol 12, pp. 201-220, 1972.
- M.M. Nigm, M.M. Sadek and S.A. Tobias, Dimensional analysis of the seady state orthogonal cutting process, Int. J. Mach. Tool Des. Res., vol. 17, pp.1-18 1977.
- M.M. Nigm, M.M. Sadek and S.A. Tobias, Determination of dynamic cutting coefficients from steady state cutting data, Int. J. Mach. Tool Des. Res., vol. 17, pp. 19-37, 1977.
- S.A. Tobias, and W. Fishwick, The chatter of the lathe tool orthogonal cutting condition, Trans. ASME J. Engng. Ind., vol. 80, No. 5., pp. 1079-1088, July 1958.
- J.S. Lin, C. and I. Weng, A nonlinear dynamic model of cutting, Int. J. Mach. Tool Manufact., vol. 30, No. 1., pp. 53-64, 1990.
- J. Gradisek, E. Govekar and I. Grabec, A chaotic cutting process and determining optimal cutting parameter values using neural networks, Int. J. Mach. Tool Manufact., vol. 36, pp. 1161-1172, 1996.
- H.M. Shi and S.A. Tobias, Theory of finite amplitude machine tool instability, Int. J. Mach. Tool Des. Res., vol. 24, 45-69, 1984.
- K. Jemelniak, and A. Widota, Numerical simulation of non-linear chatter vibration in turning, Int. J. Mach. Tools Manufact., vol. 29, No. 2., pp. 239-247, 1989.
- Y.S. Tarng, H.T. Young and B.Y. Lee, An analytical model of chatter vibration in metal cutting, Int. J. Mach. Tools Manufact., vol. 34, No. 2., 183-197, 1994.
- B.Y. Lee, Y.S. Tarng, and S.C. Ma, Modeling of the process damping force in chatter vibration, Int. J. Mach. Tool Manufact., vol. 35, No. 7., 951-962, 1995.
- Y. Kondo, O. Kawano and H. Sato, Behavior of self-excited chatter due to multiple regenerative effect, Trans. ASME J. Engng. Ind., vol. 103, pp. 324-329, August 1981.
- T. Kaneko, H. Sato, Y. Tani and M. O-hori, Self-excited chatter and its marks in turning, Trans. ASME J. Engng. Ind., vol. 106, pp. 222-228, August 1984.
- I. Kovacic, A new nonlinear dynamic model of chatter, Submitted to Int. J. Mach. Tool Manufact.
- H.E. Merrit, Theory of self-excited machine tool chatter, Trans. ASME J. Engng. Ind.Series B, vol. 87, No. 4., pp.447-454, 1965.
Приложения
Коэффициенты для выражения (6):

SAMOPOBUDNE OSCILACIJE U PROCESU REZANJA METALA
– TEORIJSKI PRILAZ
Ivana Kovacic
Ovaj rad se bavi proucavanjem pojave samopobudnih oscilacija u procesu rezanja metala. Model sistema je baziran na teorijskom pristupu deformisanja metala u zoni smicanja. Kako je dinamicka sila zavisna od vrednosti parametara rezanja, u ovom radu se razmatra uticaj koji na nju ima promena grudnog ugla i ugla smicanja tokom promene dubine rezanja, i formira modifikovani nelinearni model sile rezanja a, posledicno, i nelinearni analiticki model samopobudnih oscilacija. Analizom analitickog resenja utvrdeno je postojanje tri moguca slucaja oscilatornog kretanja alata. Za svaki od njih je numerickim putem odredena promena kompomnente sile rezanja (sile prodiranja) i grudnog ugla tokom vremena.