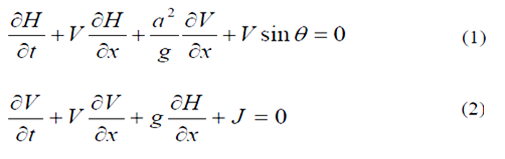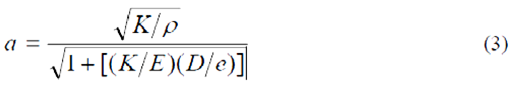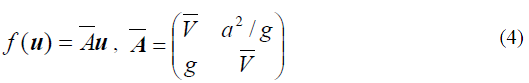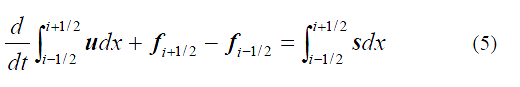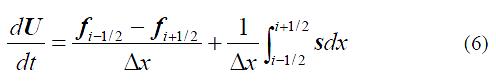Аннотация – В этой статье, схема Годунова конечного объема второго порядка применяется для проблемы гидравлических ударов и проводиться анализ результатов, которые она дает. Разработанная одномерная модель основана на решении Реймана, уравнения непрерывности в сочетании с уравнением движения, которое содержит конвективный член. Реализация граничных условий таких как: резервуары, клапаны, трубы и соединения в методе Годунова похожа с методом частиц. Эта модель применяется для двух классических проблем (систем состоящих из резервуара, трубы и клапана). Схема Годунова второго порядка устойчива для числа Куранта меньше или равного единице. Максимальное и минимальное значение полученных волн давления рассчитаны с близким соответствием с аналитическим решением и лабораторными данными.

Ключевые слова – Гидравлический Удар, Нестационарное Течение в Трубе, Конечно Объемный Метод, Решения Реймана для Метода Годунова. Второго Порядка.

I. Введение.

            В напорных трубопроводах, нарушение потока вызвано отключением насоса или резким изменением в настройках клапана, вызывает ряд прямых и обратных волн давления достаточно больших для разрыва трубопровода или повреждения других гидравлических устройств. Обратные волны давления могут привести к кавитации, булавочной или точечной коррозии. Таким образом, точное моделирование событий гидравлического удара (переходных гидравлических) крайне необходимо для правильного устройства и безопасной работы трубопроводных систем под давлением. Могут возникнуть проблемы качества воды в связи с вторжением загрязняющих веществ через трещины и швы. Качество воды затрагивается гидравлическим ударом, биопленка на трубе разрушается большими напряжением при сдвиге, вызванными переходными частицами жидкости, которые могут быть ресуспендированы сильным перемешиванием потока внутри трубы. Проектирование трубопроводных систем и прогнозирование последствий влияющих на качество воды, требует эффективной математической модели способной качественно решить проблему гидравлического удара.

           Были введены различные численные методы для переходных расчетов в трубопроводе. Они включают в себя метод характеристик (MOC), конечных разностей (FD), поверхности волны(WP), конечного объема(FV) и конечных элементов (FE). Среди этих методов, МОС оказался самым популярным у экспертов по гидравлическому удару. Подход, который использует МОС, превращает частные дифференциальные уравнения в обычные дифференциальные уравнения вдоль характеристических линий. Интеграция этих обыкновенных дифференциальных уравнений от одного временного шага к другому требует, чтобы верхнее значение и поток в нижней части каждой характеристической линии были известны. Это требование может быть выполнено одним из двух способов: 1) использование фиксированной сетки МОС метода и применение интерполяции по отношению к трубе, что невозможно для числа Куранта в точности равного единице во всех трубах. Эта интерполяция искусственно изменяет скорость волны и вводит искусственную амортизацию в решение. Метод фиксированной сетки (МОС) является наиболее широко распространенной процедурой решения уравнений гидравлического удара, он прост для кодирования, эффективен, точен и предоставляет полный контроль над выборкой сетки[1].

          Результаты решения уравнения гидравлического удара по MacCormack, Lambda и Gabutti отобразились в FD схемах, показав, что FD схемы второго порядка дают результаты лучше, чем схемы первого порядка метода МОС.

         Метод конечных элементов (FE) известен своей способностью: использовать неструктурированные сетки, обеспечивать быструю сходимость и точные результаты и дает результаты в любой точке предметной области. Тем не менее, вычисления в решениях методом конечных элементов мотивируют поисковую работу по совершенствованию численных решений. Например, Jovic использовал комбинированный метод состоящей из метода характеристик (MOC) и метода конечных элементов (FE) для моделирования гидравлического удара в классической системе (система, состоящая из резервуара, трубы и клапана) [2].

        Методы конечного объема(FV) широко используются, а решениях гиперболических систем, таких как динамика газов и поверхностные волны воды. Методы конечного объема известны своей способностью: сохранению массы и импульсов, обеспечивать высокое разделение неоднородностей без паразитных колебаний и неструктурированную сетку. Первая кратность метода конечного объема для решения гидравлического удара была сильно похожа с методом характеристик с линеаризованной пространственно-линейной интерполяцией [3]. Применение схемы Годунова для решения второго порядка, метода конечного объема для решения непрерывности и импульса уравнений без конвективного члена, приводит к точным результатам для очень малых значений чисел Маха [4].

       Цель этой статьи заключается в применении метода Годунова для FV решений нестационарных уравнений непрерывности в сочетании с уравнением движения без потерь конвективного члена (что крайне важно для случаев, когда значения чисел Маха не очень велики) и в исследовании точности разработанного метода.

       Статья построена следующим образом. Во-первых, даны основные уравнения гидравлического удара. Во-вторых, основные уравнения представляются в конечно объемной форме (FV), далее формируются системы (схемы) Годунова первого и второго порядка для FV потоков. В-третьих, получено время интегрирования уравнений. В-четвертых, схема (метод) проверена при использовании однотрубной системы. В итоге, результаты приводятся в заключительной части статьи.

II. Основные уравнения.

        Нестационарный замкнутый поток в трубе часто описывается набором одномерных (1D) гиперболических частных производных уравнений [5].

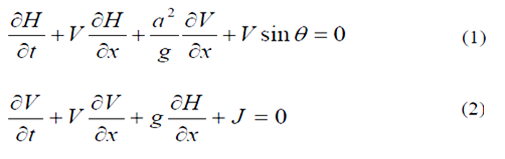
         Где t – время; x – расстояние вдоль центра трубы; H=H(x,t) – пьезометрический напор; V=V(x,t) – мгновенная средняя скорость жидкости; g – ускорение свободного падения; Ɵ – уклон трубы; j – сила трения о стенки трубы; a – скорость волны, представленная в виде:

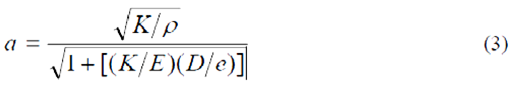
Где К – объемный модуль упругости жидкости; E – модуль Юнга упругости для труб; p – плотность жидкости и е – толщина трубы.

         Нелинейные конвективные члены V∂H / ∂x и V∂V / ∂x входят в состав уравнений (1) и (2). Хоть доля этих членов мала в разнообразии проблем связанных с гидравлическим ударом, ими не пренебрегают в этой статье. Сохранение наличия конвективных членов в основных уравнениях, делает схему (метод) применимой к широкому спектру проблем неустановившегося потока.

III. Постановка конечных объемов.

        Расчетная сетка предполагает дискретизацию оси х, длина шага дискретизации Δx , ось t делиться на интервалы, длина которых Δt. Узел (i,n) обозначает точку с координатами x = [i − (1/ 2)]  Δx и t = nΔt. Величины с индексом i и индексом n означают, что эта величина оценивается в узле (i,n).

Рис 1. Образец предельного объема (тома).

        Первый управляющий том (объем) сосредоточенный в узловой точке i и расширяется от i-1/2 до i+1/2. Поэтому первый управляющий том (объем) описывается интервалом [(i-1) Δx ,iΔx]. Граница между управляющим томом (объемом) i и управляющим томом(объемом) i+1 имеет координаты iΔx, она называется поверхностью управления или интервал (ячейка) поверхности раздела. Значение в ячейке поверхности раздела идентифицируется интервалом i-1/2 и i+1/2 (Рис 1).

       Обоснование Реймана на основе FV решения уравнений (1) и (2) в ith управляющем томе (объеме) включает следующие шаги: основные уравнения переписаны в форме управляющего тома (объема), потоки на поверхности управления аппроксимированы при помощи решения проблем Реймана, время интеграции для нахождения решения в интервале от n до n+1 [6]. Уравнения (1) и (2) могут быть переписаны в консервативной форме:

       V обозначает среднее значение и будет определено позднее. При значение V=0, схема возвращается к классическому состоянию гидравлического удара, в котором пренебрегают конвективными членами.

       Формулы массы и импульса для управляющего тома (объема) i получены путем интегрирования уравнения (4) по отношению к x от поверхности управления i-1/2 до поверхности управления i+1/2. Результат имеет следующий вид:

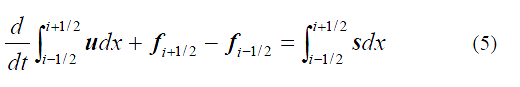
       Уравнение (5) описывает законы сохранения массы и импульса для итого управляющего тома (объема). Допускаем что Ui равно среднему значению интервала u в интервале [i-1/2,i+1/2]. Тогда, уравнение (5) имеет вид:

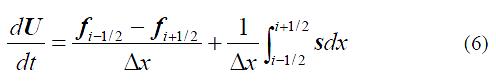
        Поток в интервале поверхности раздела может быть определен из схемы Годунова, которая требует точного решения проблемы Реймана. Схемы Годунова консервативны, точны и эффективны. Разработка схемы Годунова для массы и потока импульса fi+1/2 в уравнении для всех i и для t ∈[tn , tn+1 ] требует точного решения проблемы Реймана.