Разработка алгоритмов поиска кратчайшего пути.
Авторы: Camil Demetrescu1 and Giuseppe F. Italiano
Перевод: Черненко В.А.
Источник: http://www.dis.uniroma1.it/~demetres/docs/wea04.pdf
Авторы: Camil Demetrescu1 and Giuseppe F. Italiano
Перевод: Черненко В.А.
Источник: http://www.dis.uniroma1.it/~demetres/docs/wea04.pdf
В статье рассмотрена основная проблема в графах - нахождение кратчайшего пути. Описано взаимодействие теоретических и практических аспектов при использовании простого алгоритма Дейкстры для поиска кратчайшего пути. Показано, что изученные эвристики, которые эффективны на практически, могут уступить результатам комбинаторных свойств проблемы, и в конечном счете могут привести к новым теоретически эффективным алгоритмам.
Изучение эффективных компьютерных программ для решения задачи поиска оптимального пути привел к большому интересу относительно экспериментальных исследований алгоритмов. При создании эффективных реализаций необходимо учитывать следующее: иерархию памяти, множители в границах производительности, импликацию коммуникационной сложности, числовую точность и использование эвристики, которые иногда пропускаются в классических аналитических моделях. С другой стороны, разработка и оценка эвристики, а так же программирование методов, которые эффективны на практике, являются трудной задачей, требующая глубокого понимания математической структуры и комбинаторных свойств. В этом контексте эксперименты могут привести к новым догадкиам и теоретическим вопросам, открывая неизведанные направления исследований, которые могут привести в дальнейшем к теоретическим улучшениям и в конечном счете к более практическим алгоритмам. Целый процесс разработки, анализа, реализации, настройки, отлаживания и экспериментальной оценки алгоритмов называется Разработкой Алгоритма. Как показано на рисунке 1, разработка алгоритма – циклический процесс: разработка алгоритмических методов и анализ их производительности согласно теоретической модели обеспечивают основу для создания эффективных компьютерных программ. С другой стороны, анализ производительности программы может быть полезным в определении слабых мест в коде, разрабатывании эвристики, совершенствовании теоретического анализа и даже в изобретении более реалистических моделей стоимости, чтобы получить более глубокое понимание проблемы. [4].
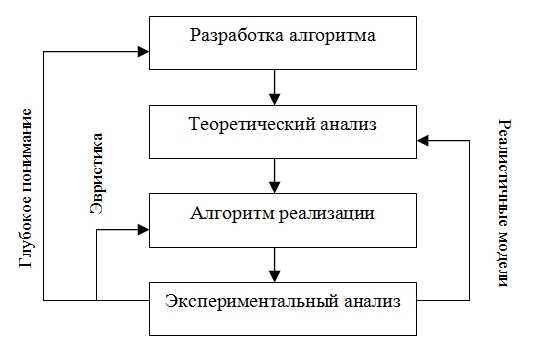
Рис. 1. Цикл разработки алгоритма.
В основе статьи собственный опыт по изучению основного принципа проблемы на графах - поиска оптимального пути. Рассматривается взаимодействие между теорией и практикой в разработке варианта поиска кратчайшего пути алгоритмом Дейкстры. В частности представлена простая эвристика, которая может существенно улучшить практическую производительность алгоритма во многих типичных проблемах. Затем показано, что более глубокое исследование этой эвристики может дать интересные комбинированные свойства путей в графе. Удивительно, использование таких свойств может привести к новым теоретически эффективным методам для того, чтобы обновить кратчайшие пути в графе, подвергающиеся изменению веса в динамике.
В 1959 Эдсгер Дейкстра разработал простой алгоритм для того, чтобы вычислять кратчайшие пути в графе [6]. Несмотря на последние достижения в области структур данных, которые привели к более быстрым реализациям (см., например, кучи Фибоначчи Фридмана [7]), алгоритмическое изобретение Дейкстры все еще актуально спустя 45 лет, обеспечивая повсеместно стандартный алгоритм эффективного поиска кратчайшего пути. Основной метод вычисляет кратчайшие пути из данной исходной вершины за время O(m+n log n), время худшего случая в графе с n вершинами и m ребрами. Чтобы вычислить все пары кратчайшего пути, мы получаем O(mn + n2 log n), в худшем случае просто повторяется алгоритм одного источника от каждой вершины.

Рис. 2. Алгоритм Дейкстры. w (x, y) обозначает вес вершины(x, y) в G.
На рисунке 2 показан простой вариант алгоритма Дейкстры, где все пары кратчайшаго пути вычислены поочередно. Алгоритм использует матрицу d, которая соответствует верхней границе расстояния в графе. Верхняя граница d [x, y] для любой пары из вершины (x, y) первоначально равно граничному весу w (x, y), если есть ребро между x и y, и +∞ в противном случае. Алгоритм также поддерживает приоритетную очередь H каждой пары (x, y) с приоритетом d [x, y]. Основной цикл алгоритма неоднократно извлекает из H пару (x, y) с минимальным приоритетом и совершает попытку к расширению при каждой итерации соответствующего кратчайшего пути ровно на одно ребро во все возможные направления. Это требует сканирования всех ребер, покидая y и используя x, выполняя классический релаксационный шаг, чтобы уменьшить верхние границы расстояния d. Не трудно доказать, что если граничные веса неотрицательны, d содержит точные расстояния. Время, необходимое для загрузки и разгрузки приоритетной очереди в худшем случае равно O(n2 log n). Каждое ребро отсканировано за время O(n), и для каждой отсканированной вершины мы тратим постоянное время, если H – например, куча Фибоначчи, это равно O(mn + n2 log n), время худшего случая.
В то время как более быстрые алгоритмы существуют для очень разбросанных графов [8 – 10], алгоритм Дейкстры, кажется, все еще хороший практический выбор для решения многих задач. Поэтому поиски быстрых реализаций привели исследователей к изучию методы для ускорения алгоритма Дейкстры на основе приоритетных очередей. Например, теперь понятно, что эффективные структуры данных играют важную роль в случае разбросанных графов, в то время как граничное сканирование имеет типичные слабые места в густых графах [1]. В остальной части этого раздела мы фокусируемся на алгоритме рисунка 2, и мы исследуем эвристические методы для того, чтобы сократить количество проверяемых вершин.

Рис. 3. Расширение кратчайшего пути от x до y одного ребра.
Рассмотрим строку 7 из рисунка 2 (или, аналогично, строка 11): цикл сканирует все ребра (y, z), ищет предварительные кратчайшие пути вида х→у→z c весом d [x, y] + w (y, z). Нужно ли нам сканировать все ребра (y, z), оставляя у? Пусть πxy кратчайший путь из х в у, и пусть πxy = πxy • (y, z) получены путем перехода от х к у через xy, и от y к z через ребро (y, z) (см. рисунок 3). Рассмотрим теперь известное свойство оптимальной подструктуры кратчайших путей (см. например, [2]):
Лемма 1. Каждый подпуть кратчайшего пути – кратчайший путь.
Это свойство подразумевает, что, если πxy – кратчайший путь и мы удаляем любой из его конечных точек мы все еще получаем кратчайший путь. Таким образом ребро (y, z) может быть последним ребром кратчайшего пути πxy, только если и πxy ⊂ πxy и πaz ⊂ πxy являются самыми короткими, где (x, a) первое ребро в πxy. Давайте теперь использовать это свойство в нашем алгоритме поиска кратчайшего пути во избежании сканирования "ненужных" ребер. Предположем, что кратчайший путь в графе является уникальным. Мы можем просто поддержать для каждой пары вершин (x, y) список ребер
Rxy = {(y, z) πxy = πxy • (y, z), кратчайший путь}, и список ребер
Lxy = {(z, x) πzy = (z, x) • πxy – кратчайший путь},
где πxy кратчайший путь от x до y. Такие списки могут быть легко созданы, так алгоритм работает на каждой паре извлечения из приоритетной очереди H. Допустим, необходимо изменить строку 7 и строку 11 из рисунка 2, чтобы отсканировать просто ребра в Ray и Lxb, соответственно, где (x, a) первая точка и (b, y) последняя точка в πxy. Не трудно увидеть, что таким образом мы рассматриваем на релаксационном шаге только пути, которые являются подпутями кратчайших путей. Назовем такие пути локально кратчайшими [5]:
Определение 1. Путь xy является локально самым коротким в G если также:
1. xy состоит из единственной вершины, или
2. каждый надлежащий подпуть xy – кратчайший путь в G.
С модификациями выше, алгоритм требует O (|LSP | + n2, log n), времени в худшим случае, где |LSP | является числом локально кратчайших путей в графе. И естественным вопросом будет: сколько локально кратчайших путей может быть в графе?
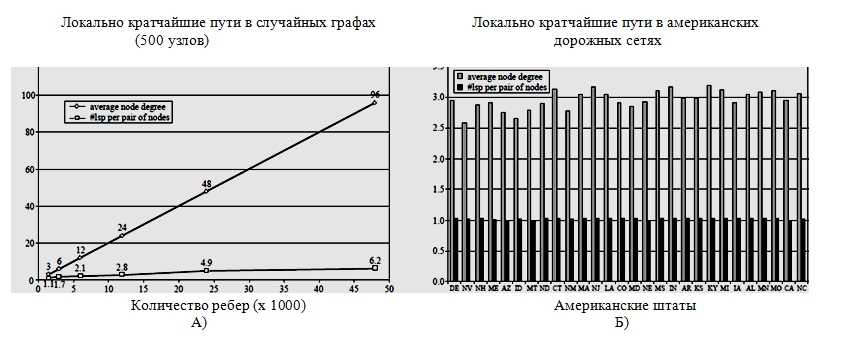
Рис. 4. Среднее число локально кратчайших путей, соединяющих пару вершин в: (А) сеть случайных графов с увеличивающейся плотностью; (Б) комплект американских дорожных сетей
Лемма 2. Если кратчайшие пути уникальны в G, то может быть не более mn локально кратчайших путей в G.[5]
Это означает, что наша модификация алгоритма Дейкстры не производит асимптотически более быстрый метод. В работе [3], произведен некоторый подсчет экспериментов и на случайных и на реальных графах (включая дорожные сети и интернет – подграфы Автономных систем), и мы обнаружили, что в этих графах |LSP | на удивление очень близко к n2. На рисунке 4 показано среднее количество локально кратчайших путей, соединяющих пары вершин в сети случайных графов с 500 вершинами и растущее число ребер, а в США набор дорожных сетей. На рисунке 5 мы сравниваем фактическое время работы алгоритма приведенного на рис 2 (S – DIJ), и тот же алгоритм, с локальной эвристической кратчайшего пути (S – LSP). Наши реализации описаны в [3]. Обратите внимание, что в случайном графе с плотностью 20% S – LSP может быть в 16 раз быстрее, чем S – DIJ. Это подтверждает наши ожидания основанные на подсчете результатов, приведенных на рисунке 4. В очень разреженных графах, S – LSP кажется немного медленнее, чем S – DIJ из–за издержек структуры данных поддержания списков Lxy и Rxy для каждой пары вершин х и у.
Рассмотрим сценарий, в котором входной граф изменяется в течении долгого времени, подвергаясь последовательности граничного обновления веса. Цель динамического алгоритма поиска кратчайшего пути - это обновление расстояния в графе эффективнее, чем перерасчет всего решения с нуля после каждого изменения веса ребра.
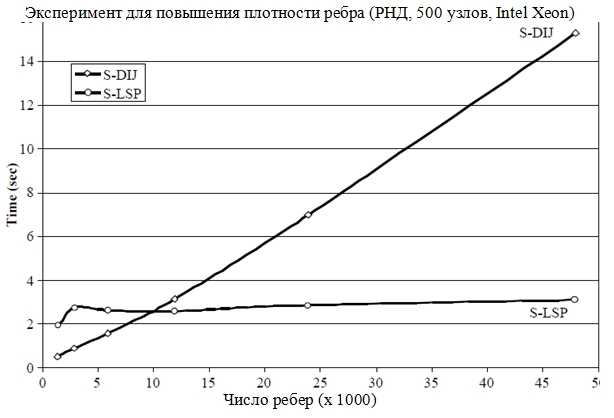
Рис. 5. Сравнение фактического времени выполнения реализации алгоритма Дейкстры с (S – LSP) и без (S – DIJ) локально кратчайшим эвристическим семейством случайных графов с 500 вершинами, при увеличении граничной плотности и веса ребра на [1, 1000]. Эксперименты выполнялись на Intel Xeon 500MHz, 512 КБ L2 кэш, RAM 512 МБ.
Идея использования локально кратчайшие пути, которая оказывается полезной для вычисления всех пар кратчайших путей, как показано в разделе 2, может сыграть решающую роль в разработке асимптотически быстрых алгоритмов обновления для динамического решения этой проблемы. Рассмотрим случай когда вес ребер может быть увеличен (уменьшен). Обратим внимание, что после увеличения веса ребра, некоторые из кратчайших путей содержащих это ребро, могут перестать быть самыми короткими, в то время как другие пути могут стать самыми короткими, заменяя старые. Цель динамического обновления алгоритма – эффективно находить такие пути замены. Локально кратчайший путь является или самым коротким или нет. Поэтому локально кратчайшие пути являются наиболее подходящими для того, чтобы стать заменой после граничного увеличения веса. Один из возможных подходов имеет в структуре данных все локально кратчайшие пути, так, чтобы замена пути могла быть найдена максимально быстро после обновления ребра. С другой стороны, хранение таких структур данных не должно быть затруднительным. То есть, в первую очередь необходимо понять сколько путей могут быть локально кратчайшими и сколько путей могут перестать быть локально кратчайшими после увеличения веса ребра?
Теорема 2. Пусть G граф с последовательным увеличением веса ребер. Если
кратчайшие пути уникальны в G, то при каждом обновлении:
1. O (n2) пути могут перестать быть локально кратчайшими;
2. O (n2) пути могут быть локально кратчайшими, за Ω(n) операций.[5]
В соответствии с теоремой 1, возможно сохранение явного множества локально кратчайших путей в графе за квадратичное амортизируемое время на операцию. Если кратчайший путь в графе локально кратчайший, то сохранение такого набора позволит нам хранить информацию и о кратчайших путях. Действительно, динамический вариант алгоритма приведенный на рис 2, показывает возможность обновления локального кратчайшего пути (и, следовательно, кратчайшего пути) графа за время O(n2 log n) с учетом увеличения веса [5]. Для графов с ребрами m = Ω(n log n), это асимптотически быстрее, чем пересчет решения с нуля, используя алгоритм Дейкстры. Кроме того, если матрица расстояний должна сохраняться явно, это лишь полилогарифмический фактор далеко не наилучший.
Для нахождения всех пар кратчайших путей в динамике в общем случае, где последовательность обновления может содержать увеличение и уменьшение, локально кротчайший путь не может быть использован непосредственно. Действительно, если увеличение и уменьшение могут быть перемешаны, возможен наихудший случай с Ω(mn) изменений в наборе локально кратчайших путей во время каждого обновления. Однако, используя обобщение из локально кратчайших путей, которое содержит историю последовательности обновления чтобы справиться с патологическими экземплярами, разработан метот, для обновления кратчайшего пути за время обновления O(n2 log3 n) [5]. Эта оценка была улучшина на O(n2 • (log n + log2(m/n))) по Thorup [11].
В статье описана методика резработки алгоритмов кратчайших путей на основе алгоритма Дейкстры. Взаимодействие между теорией и практикой привело к существенным результатам. Введено понятие локально кратчайших путей, что позволило улучшить производительность алгоритма Дейкстры для нахождения кратчайшего пути в графе. Несмотря на то, что проблема кратчайших путей изучается достаточно долгое время, на некоторые вопросы однозначно дать ответ нельзя, требуются дополнительные исследования. Например, можем ли мы вычислить все пары кратчайших путей в О(mn) графах с густой сетью? Другая интересная нерешенная проблема, возможно ли обновлить дерево кратчайших путей асимптотически быстрее, чем пересчетать его с нуля после граничного изменения веса?
1.B.V. Cherkassky, A.V. Goldberg, and T. Radzik. Shortest paths algorithms: Theory and experimental evaluation. Mathematical Programming, 73:129–174, 1996.
2. T.H. Cormen, C.E. Leiserson, R.L. Rivest, and C. Stein. Introduction to Algorithms. McGraw – Hill, 2001.
3. C. Demetrescu, S. Emiliozzi, and G.F. Italiano. Experimental analysis of dynamic
all pairs shortest path algorithms. In Proceedings of the 15th Annual ACM – SIAM
Symposium on Discrete Algorithms (SODA’04), 2004.
4. C. Demetrescu, I. Finocchi, and G.F. Italiano. Algorithm engineering. The Algo –
rithmics Column (J. Diaz), Bulletin of the EATCS, 79:48–63, 2003.
5. C. Demetrescu and G.F. Italiano. A new approach to dynamic all pairs shortest
paths. In Proceedings of the 35th Annual ACM Symposium on Theory of Computing
(STOC’03), San Diego, CA, pages 159–166, 2003.
6. E.W. Dijkstra. A note on two problems in connexion with graphs. Numerische
Mathematik, 1:269–271, 1959.
7. M.L. Fredman and R.E. Tarjan. Fibonacci heaps and their use in improved network
optimization algorithms. Journal of the ACM, 34:596–615, 1987.
8. S. Pettie. A faster all – pairs shortest path algorithm for real – weighted sparse graphs.
In Proceedings of 29th International Colloquium on Automata, Languages, and
Programming (ICALP’02), LNCS Vol. 2380, pages 85–97, 2002.br>
9. S. Pettie and V. Ramachandran. Computing shortest paths with comparisons and
additions. In Proceedings of the 13th Annual ACM – SIAM Symposium on Discrete
Algorithms (SODA’02), pages 267–276. SIAM, January 6–8 2002.
10. S. Pettie, V. Ramachandran, and S. Sridhar. Experimental evaluation of a new
shortest path algorithm. In 4th Workshop on Algorithm Engineering and Experi –
ments (ALENEX’02), LNCS Vol. 2409, pages 126–142, 2002.
11. M. Thorup. Tighter fully – dynamic all pairs shortest paths, 2003. Unpublished
manuscript.