Общая постановка проблемы

За последние 10 лет Интернет распространился в десятки, сотни и даже в тысячи раз (в некоторых странах). И согласно последним данным — сегодня каждый 3 человек на планете находится в интернете. Количество пользователей продолжает увеличиваться.

В тоже время объем данных, хранящихся в Интернете, вплотную приблизился к отметке в 1500 экзабайтов (1500 млрд Гб). По прогнозам аналитиков, через полтора года количество данных вырастет еще в 2 раза. Аналитики подчеркивают, что объем хранящейся в Интернете информации удваивается приблизительно каждые полтора года. Большой процент всех данных, хранящихся в Интернете, составляет геоинформация.

Геоинформационная система предназначена для сбора, хранения, анализа и графической визуализации пространственных данных и связанной с ними информации о представленных в ГИС объектах. Термин также используется в более узком смысле — ГИС как инструмент (программный продукт), позволяющий пользователям искать, анализировать и редактировать цифровые карты, а также дополнительную информацию об объектах.

Но, с ростом объема данных, хранящихся в Интернете, возникли проблемы визуализации большого объема пространственных данных.

В наше время, наиболее распространенной геоинформационной системой является Google Maps. Но и в данной системе существуют свои проблемы с отображением большого количества пространственных данных. Отображение геоинформационных данных может занять большое количество времени — даже для высокоскоростного Интернета такие операции могут стать серьезным испытанием, не говоря уже о скорости подключения у среднестатистического пользователя. Одним из решений данной проблемы является кластеризация.

На данный момент существует большое количество методов кластеризации, использующих разные меры и метрики. Но, несмотря на это, проблема актуальна, разрабатываются новые алгоритмы и подходы. Данная проблема достаточно сложная, поэтому полностью не решена, так как для каждой задачи необходимо выбрать соответствующий алгоритм и меры расстояний. Выбор метрики полностью лежит на исследователе, поскольку результаты кластеризации могут существенно отличаться при использовании разных мер.

Исследования

Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных групп должны быть отличны друг от друга. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.[4]

Кластерный анализ выполняет следующие основные задачи:

• Разработка типологии или классификации.
• Исследование полезных концептуальных схем группирования объектов.
• Порождение гипотез на основе исследования данных.
• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Независимо от предмета изучения, применение кластерного анализа предполагает следующие этапы:

• Отбор выборки для кластеризации.
• Определение множества переменных, по которым будут оцениваться объекты в выборке.
• Вычисление значений той или иной меры сходства между объектами.
• Применение метода кластерного анализа для создания групп сходных объектов.
• Проверка достоверности результатов кластерного решения.

Кластерный анализ предъявляет следующие требования к данным:

• показатели не должны коррелировать между собой.
• показатели должны быть безразмерными.
• распределение показателей должно быть близко к нормальному распределению.
• показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов.
• выборка должна быть однородна, не содержать «выбросов».

После получения и анализа результатов возможна корректировка выбранной метрики и метода кластеризации до получения оптимального результата.

Цели кластеризации:

• Понимание данных, путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).
• Сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
• Обнаружение новизны (англ. Novelty detection). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.[1]

Классификация кластеризации

Классифицировать алгоритмы кластеризации в широком смысле можно на два следующих класса.

1. Иерархические и плоские.

Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Таким образом, на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.

Так как основное требование к системе это быстродействие, то расчет иерархическими методами с вложенными кластерами только усложнит и замедлит процесс отображения пространственных данных.

Плоские алгоритмы строят одно разбиение объектов на кластеры.

Плоские алгоритмы считаются достаточно быстрыми и простыми в действии, что полностью отвечает поставленным требованиям. К тому же однократное разбиение позволяет избежать необходимости хранить большое количество промежуточных данных.

2. Четкие и нечеткие.

Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, то есть каждый объект принадлежит только одному кластеру.

Так как основным признаком объектов в кластерах является их географическое положение, то четкая кластеризация наилучшим образом решит проблему разделения объектов на четкие группы.

Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. То есть, каждый объект относится к каждому кластеру с некоторой вероятностью.

При работе с пространственными данными основной целью является наглядность геоинформации, поэтому, если один и тот же объект будет входить в разные кластеры, это значительно усложнит работу и запутает пользователя.

Меры расстояния между объектами

Существуют основные этапы распределения объектов по кластерам. Для начала необходимо составить вектор характеристик для каждого объекта — как правило, это набор числовых значений. Однако существуют также алгоритмы, работающие с качественными (категорийными) характеристиками.

В данном случае вектор характеристик будет хранить географические координаты пространственных данных.

После того, как мы определили вектор характеристик, можно провести нормализацию, чтобы все компоненты давали одинаковый вклад при расчете «расстояния». В процессе нормализации все значения приводятся к некоторому диапазону, например, [–1, –1] или [0, 1].

Для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик, вот лишь основные из них:

1. Евклидово расстояние.

Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:


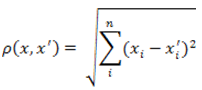
Рисунок 1 — Формула Евклидового расстояния



2. Квадрат евклидова расстояния.

Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:


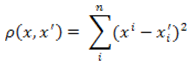
Рисунок 2 — Формула квадрата Евклидового расстояния



3. Расстояние городских кварталов (манхэттенское расстояние).

Это расстояние является средним разностей по координатам. В большинстве случаев, эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако, для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:


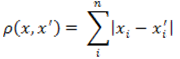
Рисунок 3 — Формула расстояния городских кварталов



4. Расстояние Чебышева.

Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой–либо одной координате. Расстояние Чебышева вычисляется по формуле:


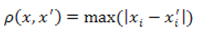
Рисунок 4 — Формула расстояния Чебышева



5. Степенное расстояние.

Применяется в случае, когда необходимо увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле:


Рисунок 5 — Формула степенного расстояния



Выбор метрики полностью лежит на исследователе, поскольку результаты кластеризации могут существенно отличаться при использовании разных мер.

Для данного случая наиболее подходящее «расстояние» — Евклидово, так как данная мера идеально подходит для расчета географических расстояний. Остальные «расстояния» менее подходящие, так как они решают специфические задачи, которые только усложнят кластеризацию пространственных данных.

Алгоритм кластеризации

Исходя из требований к системе и выбранных предпочтений, можно определиться с конкретным алгоритмом кластеризации.

Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:


Рисунок 6 — Формула среднеквадратической ошибки разбиения



Алгоритмы квадратичной ошибки относятся к типу плоских алгоритмов. Самым распространенным алгоритмом этой категории является метод k–средних. Этот алгоритм строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:

1. Случайно выбрать k точек, являющихся начальными «центрами масс» кластеров.
2. Отнести каждый объект к кластеру с ближайшим «центром масс».
3. Пересчитать «центры масс» кластеров согласно их текущему составу.
4. Если критерий остановки алгоритма не удовлетворен, вернуться к п. 2.



Рисунок 7 — Метод k–средних



В качестве критерия остановки работы алгоритма обычно выбирают минимальное изменение среднеквадратической ошибки. Так же возможно останавливать работу алгоритма, если на шаге 2 не было объектов, переместившихся из кластера в кластер.

К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения, но в данном случае это можно считать положительным свойством данного метода.

Метод k–средних также называют быстрым кластерным анализом, исходя из названия, можно определить, что данный метод наиболее подходящий для кластеризации пространственных данных. Так вычислительная сложность метода k–средних — O(nkl), где k — число кластеров, l — число итераций. Данный метод полностью отвечает поставленным требованиям: быстродействие, четкость распределения по кластерам. Также благодаря возможности изначально задавать число кластеров можно рассчитать оптимальное количество отображаемых объектов.[2:3].

Выводы

Так как основной задачей является сокращение количества отображаемых пространственных объектов без потери данных, основной целью кластеризации является понимание данных, путём выявления кластерной структуры. Так как она имеет преимущество, которое заключается в том, что число кластеров необходимо стараться сделать меньше.

Для эффективного решения данной проблемы необходимо реализовать алгоритм, который относится к плоской кластеризации, так как не будет необходимости во вложенных кластерах. Всю выборку пространственных данных необходимо единожды разбить на кластеры.

Также алгоритм должен относиться к четкой кластеризации, так как пересечение кластеров недопустимо. Один пространственный объект будет относиться только к одному кластеру.

Чтобы определить степень «похожести» пространственных объектов на основе их положения на карте, необходимо использовать Евклидово расстояние как меру расстояния между объектами для объединения их в кластеры.

По данным сравнительного анализа основных алгоритмов кластеризации можно сделать вывод, что наиболее подходящим алгоритм для разбиения на кластеры пространственных данных является алгоритм квадратичной ошибки. А именно, метод k–средних.

Данный метод наиболее эффективно минимизирует количество отображаемых данных без потери информации. Недостаток метода — необходимость указывать количество кластеров, никак не повлияет на результаты работы.

Остальные алгоритмы только усложнят работу, увеличат время обработки данных и нагрузку на трафик.

В целом, можно сказать, что кластеризация — наиболее эффективное решение проблемы отображения большого количества пространственных данных, так как данный метод позволит компактно распределить необходимую информацию без потери данных. Данное решение в большой мере повлияет на скорость работы геоинформационной системы, а следовательно и уменьшит затраты времени пользователя.

Литература

1. Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. Курс лекций. МГУ, 2007.
2. Jain A., Murty M., Flynn P. Data Clustering: A Review. // ACM Computing Surveys. 1999. Vol. 31, no. 3.
3. Котов А., Красильников Н. Кластеризация данных. 2006.
4. Мандель И. Д. Кластерный анализ. — М.: Финансы и Статистика, 1988.
5. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989.
6. Информационно–аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных — www.machinelearning.ru/
7. Чубукова И.А. Курс лекций «Data Mining», Интернет–университет информационных технологий — www.intuit.ru/department/database/datamining/
8. Интернет энциклопедия — http://ru.wikipedia.org/wiki/Кластерный_анализ
9. Журавлев Ю. И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006.