МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Автор: Steven J. Miller
Перевод: Сиротенко Е.И.
Steven J. Miller - Метод наименьших квадратов. Метод наименьших квадратов представляет собой процедуру, определяющую наиболее подходящие ряды данных; в качестве доказательства используются простые вычислительные методы линейной алгебры. Основная задача состоит в нахождении наилучшего решения уравнения 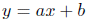 учитывая, что для
учитывая, что для 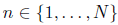 значения
значения 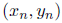 определяемые. Метод легко обобщаем для нахождения наилучшего значения из:
определяемые. Метод легко обобщаем для нахождения наилучшего значения из:
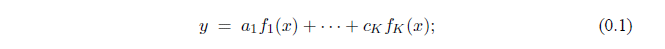
Это не является необходимым для функции 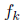 , линейной для х - все, что необходимо, это чтобы y был линейной комбинацией этих функций.
, линейной для х - все, что необходимо, это чтобы y был линейной комбинацией этих функций.
Часто в реальном мире можно найти линейные зависимости между величинами. Например, сила упругости линейно зависит от деформации тела: 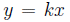 (где y - сила упругости, х - деформация тела, k - коэффициент пропорциональности). Для проверки предлагаемого соотношения исследователи в лаборатории измерили силу упругости при различных деформациях. Таким образом они собрали данные о
(где y - сила упругости, х - деформация тела, k - коэффициент пропорциональности). Для проверки предлагаемого соотношения исследователи в лаборатории измерили силу упругости при различных деформациях. Таким образом они собрали данные о 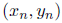 , изменяющихся от
, изменяющихся от 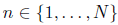 ; здесь
; здесь 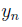 - определяемая сила в Ньютонах, когда
- определяемая сила в Ньютонах, когда 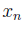 - величина деформации в метрах.
- величина деформации в метрах.
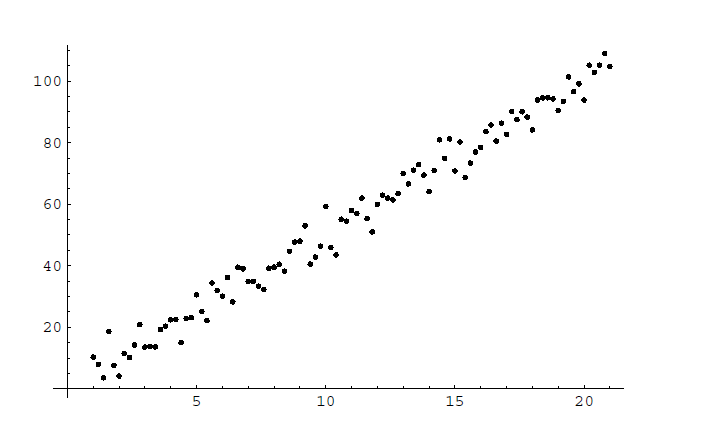
Рисунок 1 – Генератор 100 наблюдений зависимости изменения силы упругости от деформации (k=5).
К сожалению маловероятно, что мы будем наблюдать идеальные линейные зависимости. Этому есть две причины. Первая – экспериментальная ошибка; вторая – основные взаимосвязи не могут быть точно линейными, а только относительно линейными. Как видно на рисунке 1, моделируются наборы данных зависимости изменения силы упругости от деформации при коэффициенте пропорциональности равном 5.
Метод наименьших квадратов – процедура, требующая лишь некоторых вычислений линейной алгебры, позволяющая определить «наилучшее соответствие» линейной зависимости рядов данных. Конечно, нам необходимо количественное определение, того что мы подразумеваем под «наилучшим решением», для этого потребуется краткий обзор некоторых положений теории вероятности и математической статистики.
Тщательный анализ обоснования метода покажет, что он способен на значительные обобщения. Вместо того чтобы находить наиболее подходящую линию, мы могли бы найти наиболее подходящий вид любой конечной линейной комбинации указанных функций. Таким образом, общая проблема данной функции 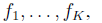 найти значения коэффициентов
найти значения коэффициентов 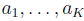 таких, что линейное соотношение
таких, что линейное соотношение
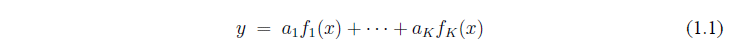
является наилучшим приближением.
Дадим краткое описание основных элементов теории вероятности и математической статистики, которые нам нужны в методе наименьших квадратов, для получения дополнительной информации см. [1, 2, 3, 4, 5, 6, 7]
Учитывая последовательность данных 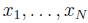 , определим среднее или ожидаемое значение
, определим среднее или ожидаемое значение 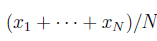 . Обозначим это. написав линию над х: таким образом
. Обозначим это. написав линию над х: таким образом
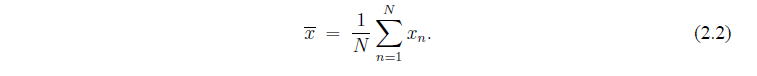
Получим среднее значение данных.
Рассмотрим следующие две последовательности данных: 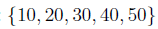 и
и 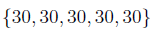 . Обе последователности содержат определенные значения, однако первый набор данных имеет больший разброс относительно среднего значения. Это приводит к понятию вариации, которое является полезным инструментом, чтобы количественно измерить насколько набор данных колеблется около своего среднего значения. Дисперсии
. Обе последователности содержат определенные значения, однако первый набор данных имеет больший разброс относительно среднего значения. Это приводит к понятию вариации, которое является полезным инструментом, чтобы количественно измерить насколько набор данных колеблется около своего среднего значения. Дисперсии 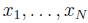 , обозначаемые
, обозначаемые 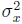 :
:
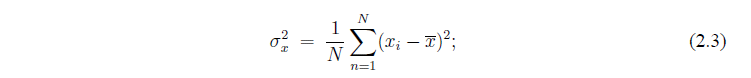
Стандартное отклонение 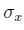 есть квадратный корень из дисперсии:
есть квадратный корень из дисперсии:
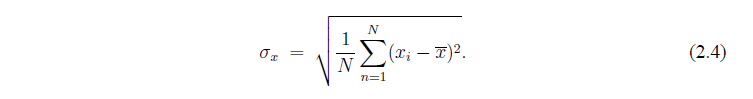
Заметим, что если единицы измерения х - метры, то дисперсия 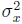 имеет единицы измерения м
имеет единицы измерения м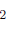 , а стандартное отклонение
, а стандартное отклонение 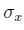 и среднее значение
и среднее значение 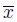 имеюи единицы измерения метры. Таким образом, стандартное отклонение дает хорошую меру отклонения х вокруг своего среднего значения.
имеюи единицы измерения метры. Таким образом, стандартное отклонение дает хорошую меру отклонения х вокруг своего среднего значения.
Конечно есть альтернативные меры, которые можно использовать.Например, можно было бы рассмотреть:
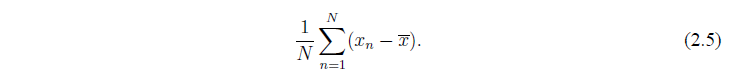
К сожалению здесь указано колличество и большие положительные отклонения могут исключать отрицательные. В самом деле, из определения среднего значения вытекает, что результат всегда больше нуля! Это затем стало бы страшной мерой разброса данных, так как оно равно нулю независимо от значений данных.
Мы можем решить эту проблему, используя абсолютные значения. Это приводит нас к рассмотрению
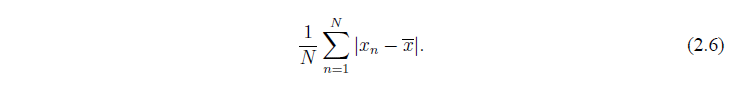
Хотя имеется преимущество, избежать наличия ошибок (в тех же единицах измерения, что и х) невозможно, функция абсолютно значения не очень хороша, как аналитическая функция. Она не дифференцируема. Это вызвано тем, что прежде всего мы вычисляем стандартное отклонение (квадратный корень из дисперсия) - это позволяет нам использовать стандартные средства исчисления.
Теперь мы можем определить количественно, что мы подразумеваем под наилучшим значением. Если мы считаем, что 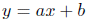 , тогда
, тогда 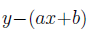 должно быть равно нулю. Таким образом, по данным наблюдений
должно быть равно нулю. Таким образом, по данным наблюдений
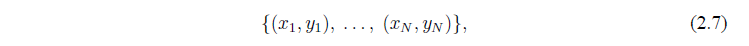
мы увидим
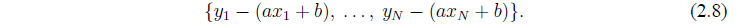
Среднее значение должно быть наибольшим (если оно подходит), а разница будет определять насколько хорошо подходящее значение у нас есть.
Следует отметить, что дисперсия для этого набора данных
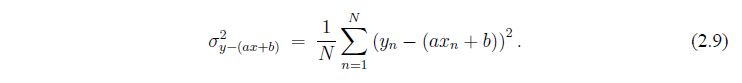
Большие ошибки имеют больший вес, чем меньшие (из-за возведения в квадрат). Таким образом, наша процедура приводит к большим средним ошибкам при наличии больших ошибок отдельных величин. Если бы мы использовали абсолютные значения измерения (см. уравнение (2.6)), то все ошибки имели бы одинаковый вес, однако абсолютные значения функции недифференцируемы, таким образом средства исчисления становятся недоступными.
Учитывая данные 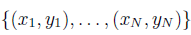 , мы можем определить ошибки, связанные с
, мы можем определить ошибки, связанные с 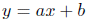 соотношением
соотношением
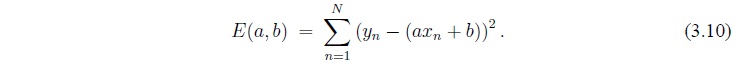
Здесь N раз значения дисперсии набора данных 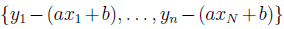 . Не имеет значения действительно ли мы изучаем дисперсию или N раз разности наших ошибок, важно, что ошибка является функцией двух переменных.
. Не имеет значения действительно ли мы изучаем дисперсию или N раз разности наших ошибок, важно, что ошибка является функцией двух переменных.
Цель состоит в том, чтобы найти значения a и b, которые минимизируют ошибки. В многомерном исчислении мы получаем, что это требует от нас найти значения (a и b) такие что
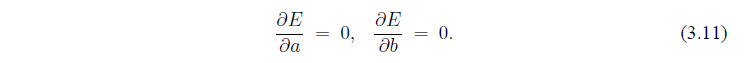
Обратите внимание, мы не должны беспокоиться о граничных точках: если 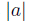 и
и 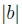 станут большими, значения подходят все хуже и хуже. Таким образом, нам не нужно проверять на границе.
станут большими, значения подходят все хуже и хуже. Таким образом, нам не нужно проверять на границе.
Дифференцирование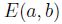 дает
дает
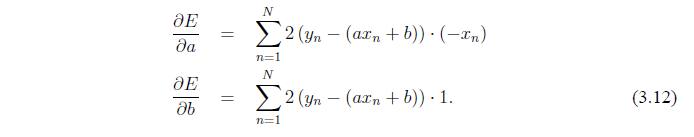
Установление 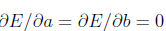 (и деления на 2) дает
(и деления на 2) дает
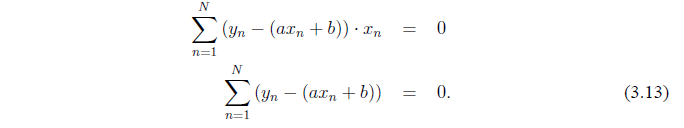
Мы можем переписать эти уравнения, как
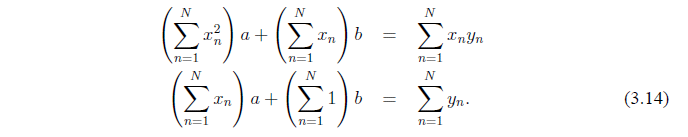
Мы получили, что значения a и b, сводящие к минимуму ошибки (определенные в (3.10)) удовлетворяют следующим матричным выражениям:
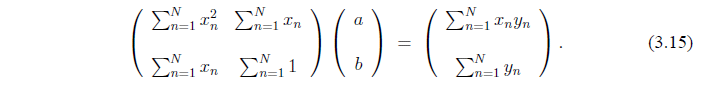
Мы покажем,что матрица обратима, что подразумевает
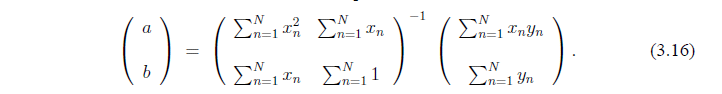
Обозначим матрицу М. Определитель М
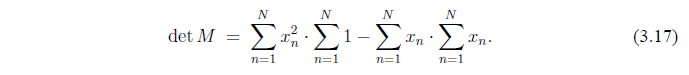
где
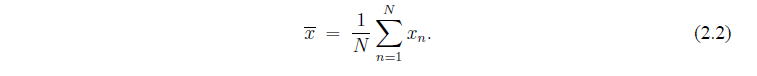
найдем что
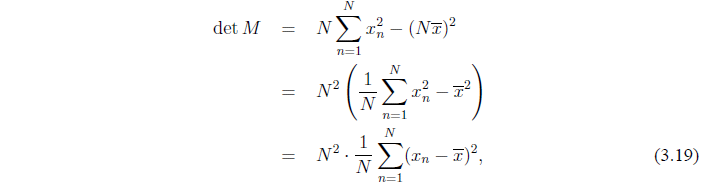
где последнее равенство следует из элементарной алгебры. Таким образом, пока все 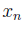 не равны
не равны 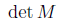 будут отличны от нуля и M будет обратима.
будут отличны от нуля и M будет обратима.
Данные на рисунке 1 получены из выражения 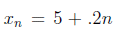 и выражения
и выражения 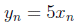 прюс ошибка, случайно сгенерированная из нормального распределения с нулевым средним значением и стандартным отклонением
прюс ошибка, случайно сгенерированная из нормального распределения с нулевым средним значением и стандартным отклонением 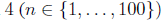 . Используя эти значения, мы найдем наилучшее соответствие линии
. Используя эти значения, мы найдем наилучшее соответствие линии
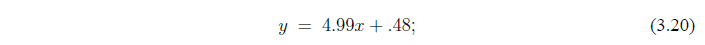
где a=4.99 и b=0.48. Как видно по соотношению 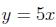 мы ожидали наилучшее значение а=5 и b=0.
мы ожидали наилучшее значение а=5 и b=0.
В то время, как наши значения а близки к истиному значению. значения b значительно отличаются от него. Мы сознательно выбрали данных такого рода для обозначения опасности при использовании метода наименьших квадратов. Только потому, что мы знаем, что 4.99 лучшее значение уклона, и 0.48 лучшее значение для y-перехвата, не означает, что это хорошие оценки истиного значения. Теория должна быть дополнена методами, которые обеспечивают оценки погрешности. Таким образом, если мы хотим узнать что-то с учетом этих данных, с вероятностью 99%, что истиное значение а находится в диапазоне (4.96 - 5.02), а истиное значение b - в диапазоне (-0.22 - 1.18); это гораздо полезнее, чем просто знать наилучшее значение.
Если бы вместо этого мы использовали
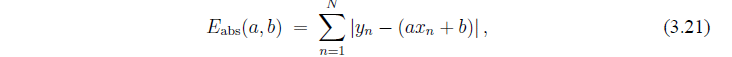
то численные методы дают, что лучше подходит значение а=5.03 и лучшее значение b меньше чем 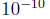 по абсолютной величине. Разница между этими величинами и полученными из метода наименьших квадратов в наилучшем значении b (наименее важный из этих двух параметров), и в связи с различными способами взвешивания ошибок.
по абсолютной величине. Разница между этими величинами и полученными из метода наименьших квадратов в наилучшем значении b (наименее важный из этих двух параметров), и в связи с различными способами взвешивания ошибок.
Обобщить метод наименьших квадратов, чтобы найти наиболее подходящий для квадратичной формы 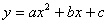 (или вообще наиболее подходящий полином степени m
(или вообще наиболее подходящий полином степени m 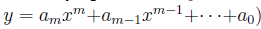 .
.
В то время как для любой реальной проблемы мира, непосредственное вычисление определяет, будет ли в результате матрица обратима, это положительный момент, так как есть возможность доказать, что определитель всегда отличен от нуля для наилучшего решения (если все х не одинаковы).
Если х не одинаковы, должен ли определитель бы отличным от нуля для наилучшего решения квадратичной или кубической формы?
Посмотрим на доказательство метода наименьших квадратов, отметим что это несущественно, если у нас есть 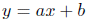 ; мы могли бы иметь
; мы могли бы иметь 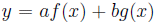 , где аргументы определены аналогичным образом. Разница в том, что мы получаем
, где аргументы определены аналогичным образом. Разница в том, что мы получаем
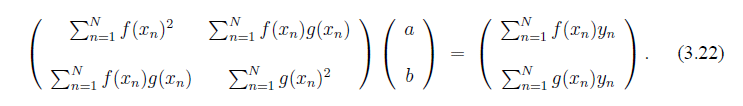
Рассмотрим обобщение метода наименьших квадратов, приведенные в (3.22). При каких условиях матрица обратима?
Метод доказательства обобщает далее случай, когда можно ожидать, что у является линейной комбинацией К определенных функций. Функции не должны быть линейными; все что необходимо - иметь линейную комбинацию, например  . Они определяются
. Они определяются 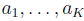 , которые минимизируют дисперсию (сумма квадратов ошибок) метолами линейной алгебры. Найдем матричное выражение, которому лучше всего подходят коэффициенты (
, которые минимизируют дисперсию (сумма квадратов ошибок) метолами линейной алгебры. Найдем матричное выражение, которому лучше всего подходят коэффициенты (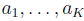 ).
).
Рассмотрим лучшее решение по методу наименьших квадратов, таким образом значения наилучшего решения получены из (3.16). Есть точка 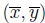 , где
, где 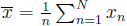 и
и 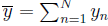 , является лучшим решением? Другими словами, лучшее решение проходит через среднюю точку?
, является лучшим решением? Другими словами, лучшее решение проходит через среднюю точку?
1. P. Bickel and K. Doksum, Mathematical Statistics: Basic Ideas and Selected Topics,
Holden-Day, San Francisco, 1977.
2. G. Casella and R. Berger, Statistical Inference, 2nd edition, Duxbury Advanced Series, Pacific Grove, CA, 2002.
3. R. Durrett, Probability: Theory and Examples, 2nd edition, Duxbury Press, 1996.
4. W. Feller, An Introduction to Probability Theory and Its Applications, 2nd edition, Vol. II, John Wiley & Sons, New York, 1971.
5. D. Kelley, Introduction to Probability, Macmillan Publishing Company, London, 1994.
6. R. Larson and B. Farber, Elementary Statistics: Picturing the World, Prentice-Hall, Englewood Cliffs, NJ, 2003.
7. D. Moore and G. McCabe, Introduction to the Practice of Statistics,W. H. Freeman and Co., London, 2003.