Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Наукова значимість роботи
- 3. Мета дослідження
- 4. Огляд досліджень та розробок
- 4.1 Огляд міжнародних джерел
- 4.2 Огляд національних джерел
- 4.3 Огляд локальних джерел
- 5. Ізоморфізм графів
- 6. Інваріанти графа
- 7. Результати магістерської роботи
- Висновки
- Примітка
- Перелік посилань
Вступ
Теорія графів в нинішній час активно застосовується в хімії, інформатиці та програмуванні, комунікаційних і транспортних системах, економіці, логістиці, схемотехніці для розв'язання різноманітних задач. Одним з найважливіших і найскладніших завдань теорії графів є знаходження топологічної еквівалентності. Це завдання в тій чи іншій мірі незмінно зачіпає всі області повпов'язані з теорією графів. Необхідно так само відзначити, що на даний момент ще не розроблено універсального, якісного і швидкого методу визначення топологічної еквівалентності вершин графа.
Складність цього завдання полягає в тому, що необхідно визначити момент, зупинки агента. У зв'язку з цією проблемою видається неможливим застосування генетичних і нейромережевих алгоритмів, що значно ускладнює процес знаходження оптимального рішення.
1. Актуальність теми
В даний час проблема топології виникає все частіше і частіше як в програмуванні, так і в хімії. Здебільшого поставлена задача розглядається програмістами, бо виникає вона при програмуванні руху робота по місцевості, якому необхідно створити карту місцевості і визначити де саме він знаходиться на місцевості, карта яка дана спочатку, або це інша місцевість і карту необхідно зберегти. Так само перевірку на бісімуляцію активно використовують при тестуванні, в мережах Петрі і LTS. Топологія є природною мовою для вивчення систем пов'язаних з побудовою схеми пов'язаності атомів в молекулі.
2. Наукова значимість роботи
В ході дослідження буде отримано алгоритм руху агента по орієнтованому графу з поміченими вершинами, який дозволить максимально спростити процес тестування з використанням LTS, а так само при порівнянні мереж Петрі на завершальному етапі розробки систем.
3. Мета дослідження
Об'єктом дослідження даної роботи є вивчення існуючих на даний момент методик визначення топології, її недоліки та переваги. В процесі дослідження будуть сформульовані базові гіпотези і закони для розробки методу визначення топологічної еквівалентності вершин графа. Даний метод дозволить розробити програмний комплекс який спростить роботу хіміків, а також дозволить звіряти результати тестування програмних комплексів швидше і ефективніше.
4. Огляд досліджень і розробок
Так як теорія графів є невід'ємною частиною тестування програмного продукту, а так само широко застосовується при розробці систем різного рівня. Проблеми виникають визначенням бісімуляції вершин графа пов'язані безпосередньо з робототехнічними системами, тобто пересуванню робота на місцевості. Ці питання широко досліджують американські, європейські і російські вчені, а так само вітчизняні фахівці в цій галузі. Питанням визначення топологічної еквівалентності вершин графа присвячений ряд робіт, головним чином, дослідників західної школи.
4.1 Огляд міжнародних джерел
У доповіді В.М. Бухштабера Торична топологія
[3]
викладено ключові результати і додатки торічної топології, як нової галузі
досліджень на стику еквіваріантной топології, комбінаторики багатогранників,
алгебраїчної, комплексної і сімплектичної геометрії, яка активно розвивається
останні 15 років. Так само це питання широко висвітлюється Т.Є. Пановим, який
займається розробками в цій галузі разом з В.М. Бухштабером [4].
В роботі В.А. Башкіна поданний метод наближення найбільшої бісімуляціі в однолічильної мережі, заснований на використанні одноперіодичної символьної арифметики і поняття розшарованої бісімуляціі [2].
Визначення топологічної еквівалентності одного типу, локальних особливостей
динамічних систем, було доведено в теоремі про топологічну еквівалентність в
роботі С.П. Горбікова Топологічна еквівалентність одного типу локальних
особливостей динамічних систем з ударними взаємодіями
[5].
4.2 Огляд національних джерел
Стаття В.П. Пінчука (Запорізький національний технічний університет) присвячена використанню базових графів для побудови топології багатопроцесорних систем. Автор пропонує метод отримання повних наборів неорієнтованих, непозначених графів, із заданими властивостями, а О.А. Пришляк (Київський університет ім. Т.Г. Шевченка) запропонований метод визначення топологічної еквівалентності векторних полів Морса-Смейла beh-2 на тривимірних многовидах [12].
Аналіз процесних алгебр та їх використання в задачах розподіленого імітаційного моделювання розглянуто в роботах С.А. Оліщук, М.А. Вовк (Харківський національний університет радіоелектроніки) [11].
4.3 Огляд локальних джерел
Статті Е.А. Пряничникова присвячені алгебрі мов представленої в графах, в них висвітлюються такі питання:
Про алгебрі мов, представимо в графах із зазначеними вершинами
в якій розглядаються властивості алгебри мов, представимо орієнтованими графами із зазначеними вершинами [16].Характеризація мов, представимо в графах c зазначеними вершинами
в якій доводиться теорема, аналогична теоремі Майхілла-Неруда для мов, які розпізнаються кінцевими автоматами. На основі доведення теореми показано, що будь-якій мові, породженої графом із зазначеними вершинами, відповідає єдиний з точністю до ізоморфізму повний детермінований граф [15].Алгебри мов, асоційовані з зазначеними графами
в якій дається визначення поняття мову, допустимому в зазначеному графі, запроваджується система операцій на формальних мовах [17].Про повноту системи аксіом для алгебри мов, які представлені кінцевими орієнтованими графами із зазначеними вершинами
в якій розробляється система аксіом алгебри мов представленої в графах із зазначеними вершинами і доводиться її повнота [14].Взаємозв'язок алгебр мов, які представлені у зазначених графах
в якій показано, що алгебра мов, яка представлена в графах із зазначеними вершинами, не є алгеброю Кліні, і між цією алгеброю і алгеброю регулярних мов немає гомоморфізму [13].- Спільно з І.С. Грунським видана стаття присвячена алгебрі мов, яка представлена графами із зазначеними вершинами. В якій висвітлюються властивості алгебри мов, які представлені орієнтованими графами із зазначеними вершинами [8].
І.С. Грунським, Е.А. Татаріновим був запропонований метод розпізнавання
кінцевого графа блукаючим по ньому агентом [7]. А також
розпізнавання лабіринту за допомогою кінцевих автоматів [6].
У співавторстві з Грунський І.С. Сапунов С.В. і Татаринов Е.А. видали статтю
Про експерименти з поміченими графами
. В якій проводиться експеримент з агентами
взаімодествіі між собою і графом [9].
5. Ізоморфізм графів
На малюнку 1 зображені два графа з однією і тїєю ж кількістю вершин {a, b, c, d}.
При уважному розгляді можна виявити, що це різні графи – в лівому є ребро (a, c),
у правому ж такого немає. У той же час, якщо не звертати уваги на найменування
вершин, то ці графи явно однаково влаштовані: кожен з них – цикл з чотирьох вершин.
У багатьох випадках при дослідженні будови графів імена або номери вершин не
рають ролі, і такі графи, один з яких виходить з іншого перейменуванням вершин,
зручніше було б вважати однаковими. Для того щоб це можна було робити
на законній підставі
, вводиться поняття ізоморфізму графів.
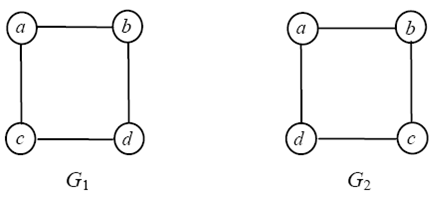
Рисунок 1 – Ізоморфні графи
Визначення. Графи G1 і G2 називаються ізоморфними, якщо існує така бієкція f множини VG1 на множину VG2, що (a, b) ∈ G1 тоді і тільки тоді, коли (f (a), f (b))∈ G2. Відображення f в цьому случаї називається ізоморфізмом графа G1 на граф G2. Той факт, що графи G1 і G2 ізоморфні, записується так: G1 ≅ G2.
Той факт, що графи G1 і G2 ізоморфні, записується так: G1 ≅ G2.
Для графів, зображених на рисунку 1, изоморфизмом є наприклад, відображення, що задається наступним чином:
x (вершина графа G1): a, b, c, d;
f(x) (вершина графа G2): a, b, d, c.
Зауважимо, що в цьому прикладі є й інші ізоморфізми, першого графа на другий. Сформульоване визначення ізоморфізму годиться і для орієнтованих графів, потрібно тільки обидві згадані в ньому пари вершин вважати впорядкованими.
Ізоморфізм – бінарне відношення на множині графів. Очевидно, це відношення рефлексивні, симетричні і транзитивні, тобто є відношеннями еквівалентності. Класи еквівалентності називаються абстрактними графами. Коли говорять, що розглядаються абстрактні графи, це означає, що ізоморфні графи вважаються однаковими. Абстрактний граф можна уявляти собі як граф, у котрого стерті імена (позначки) вершин, тому абстрактні графи іноді називають також не поміченими графами [1].
6. Інваріанти графа
У загальному випадку дізнатися, ізоморфні чи два графа, досить складно. Якщо буквально слідувати визначенням, то потрібно перебрати всі бієкції множини вершин одного з них на множину вершин іншого, і для кожної з них перевірити бієкцію, чи є вона ізоморфізмом. Для n вершин є n! бієкція і ця робота стає практично нездійсненою вже для не дуже великих n (наприклад, 20!> 2 * 1018 ). Однак у багатьох випадках буває досить легко встановити, що два даних графа не ізоморфні. Розглянемо, наприклад, графи, зображені на рисунку 2.
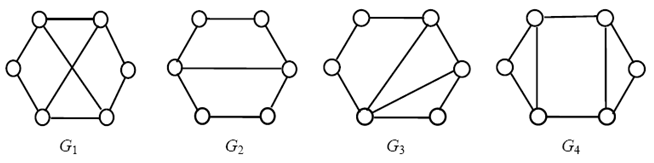
Рисунок 2 – Ізоморфні графи
Так як при ізоморфізмі пара суміжних вершин переходить в пару суміжних, а пара несуміжних – в пару несуміжних, то зрозуміло, що число ребер у двох ізоморфних графів має бути однаковим. Тому відразу можна сказати, що графи G1 і G2, у яких різна кількість ребер, не ізоморфні. У графів G1 і G3 однакове число ребер, але вони теж не ізоморфні. Це можна встановити, порівнюючи ступені вершин. Очевидно, при ізоморфізмі кожна вершина переходить у вершину тій же мірі. Отже, ізоморфні графи повинні мати однакові набори ступенів, а у графів G1 і G3 ці набори різні. З графами G1 і G4 справа йде трохи складніше – у них однакові набори ступенів. Але і ці графи не ізоморфні. Можно помітити, що в графі G4 є цикл довжини 3, а в графі G1 таких циклів немає. Ясно, що при ізоморфізмі кожен подграф одного графа переходить в ізоморфний йому подграф іншого.
Характеристики графів, які зберігаються при ізоморфізмі, називаються інваріантами. У цьому прикладі бачимо деякі прості інваріанти – число ребер, набір ступенів, число циклів заданої довжини, надалі будуть введені ще багато інших. Якщо вдається встановити, що для двох досліджуваних графів деякий інваріант приймає різні значення, то графи не ізоморфні. Для того щоб довести, що два графа ізоморфні, необхідно пред'явити відповідну бієкцію [10].
7. Результати магістерської роботи
В данній магістерській роботі будуть розглянуті і проаналізовані існуючі алгоритми визначення ізоморфізму графів. Метою даної роботи є створення більш ефективного алгоритму визначення топологічної еквівалентності і порівняння його з існуючими.
Вхід: графи G1(s) і G2(t). Графи: орієнтовані, без кратних дуг, детерміновані.
Матрицею суміжності MATRi задані графи G1 і G2, вихідні вершини s і t, L1 і L2 безліч відміток графа, Vi(G1,G2), Vn(Gn) – вершини графа, Gn – новий граф, масив нових вершин Smeg (Vn).
Вихід: Графи топологічно еквівалентні чи ні.
Метод: Будуємо Gn (Vn) по ярусах.
Алгоритм.
- Якщо L (G1) = L (G2), то переходимо до 2, інакше до 15. Граф G1 і G2 починаємо досліджувати з вершин V1(s0) і V1(t0).
- Якщо L(s)=L(t), то переходимо до 3, інакше до 15.
- Створюємо вершину графа Vn і присвоюємо їй такий же номер, як і у графа G1 і переходимо до 4.
- Побудуємо всі суміжні вершини Vi(s) і Vi(t). Будуємо стільки ребер скільки букв в алфавіті міток. Переходимо до 5.
- Якщо серед отриманих результатів буде Vsi=0 і Vti=Vi(t) або Vsi=Vi(s) і Vti=0, то переходимо до 15, інакше 6.
- Якщо лист Vsi=0 и Vti=0 то видаляємо поперечні і зворотні ребра, і вершину, інакше 7.
- Якщо листи в графі Gn повторяютcя то переходимо до 8, інакше 12.
- Склеюємо вершини Vn(si,ti)=Vn(si,ti) ) і преходимо до 9.
- Зберігаємо номера вершин Vsi , Vti і мітку вершини L графа G1 в масив нових вершин Smeg (Vn) і переходимо до 10.
- Заповнюємо матрицю суміжності MatrGn і переходимо до 11.
- Якщо з Vi не можна побудувати новий ярус, то переходимо до шагу 12, інакше 4.
- Переміщаємося на ярус тому і перевіряємо, чи можемо з будь-якої вершини
побудувати ярус. Якщо
так
то переходимо до 4. Якщоні
, то так рухаємося поки не потрапимо в початок, і переходимо до кроку 13. - Якщо G1=Gn переходимо до 14, інакше 15.
- Графи топологічно еквівалентні.
- Графи топологічно не еквівалентні.
В загальному вигляді процес роботи алгоритму показаний на малюнку 3.
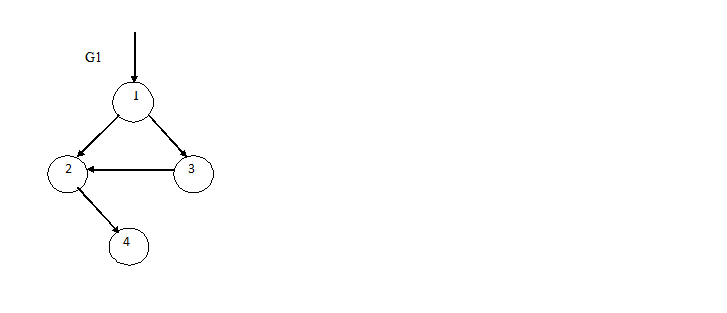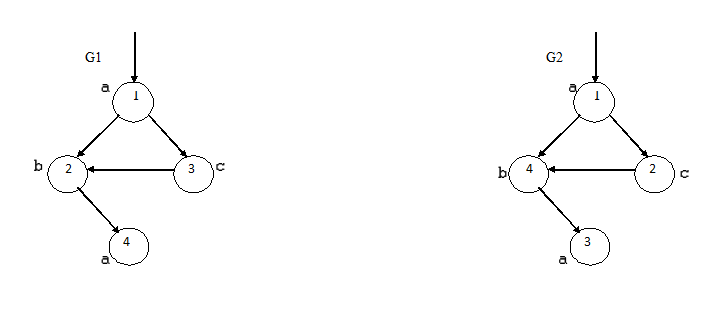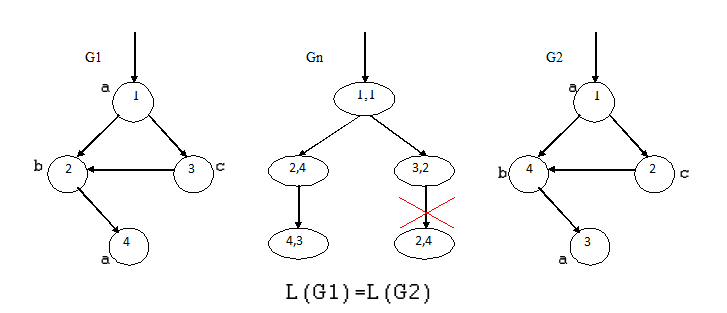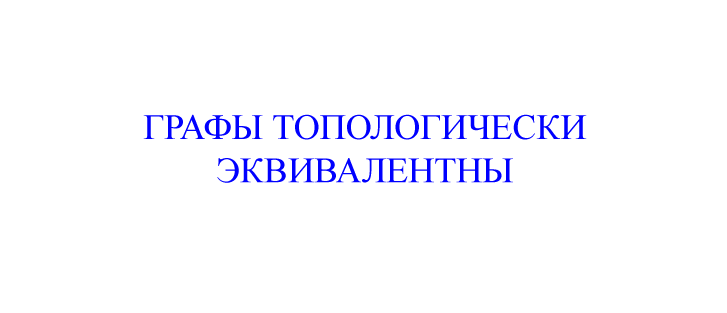
Рисунок 3 – Алгоритм визначення топологічної еквівалентності
(анімація: 8 кадрів, 10 циклів повторення, 30,4 кілобайт)
(G1 и G2 – графи, Gn – граф відображає топологічну еквівалентність G1, G2)
Висновки
Розроблювальний алгоритм є одним з напрямків теорії графів, а саме ізоморфізм графів і представляє не тільки теоретико-дослідний, але і практичний інтерес. Розробка алгоритму відкриє шлях до більш широкого застосування теорії графів при проектуванні робототехніки.
Магістерська робота присвячена актуальній науковій задачі об'єднання основних методів визначення ізоморфізму графів і алгебри мови розмітки. У рамках проведених досліджень отримані наступні результати:
- Досліджені основні принципи ізоморфізму.
- Розроблена постановка задачі.
- На підставі аналізу літературних джерел виділено основні алгоритми, які можуть бути використані в запропонованому підході до визначення біссімуляцї дерев.
Подальші дослідження спрямовані на доопрацювання базових алгоритмів під задану специфікацію, визначення меж ефективності розробленого алгоритму,проведення математичного розрахунку витрат часу і пам'яті на реалізацію.
Примітка
При написанні даного автореферату випускна робота ще не завершена. Остаточне завершення: січні 2013. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список джерел
- Алексеев В.Е. Графы. Модели Вычислительных структур данных / В.Е. Алексеев, В.А. Таланов. – Нижний Новгород. : НижГУ, 2004. – 294 с.
- Башкин В.А. Построение приближений бисимуляции в одноточечных сетях / В.А. Башкин // Труды конференции «Моделирование и анализ информационных систем» – Ярославль: Ярославский государственный университет им. Демидова, 2011. – С. 34–44
- Бухштабер В.М. Торическая топология / В.М. Бухштабер // Общеинститутский семинар « Математика и ее приложения» М : Институт им. В.А. Стеклова, 1990. – 35 с.
- Бухштабер В.М. Торические действия в топологии и комбинаторике / В. М. Бухштабер, Т. Е. Панов – М : МЦ-НМО, 2004. – 272 с.
- Горбиков С.П. Топологической эквивалентности одного типа локальных особенностей динамических систем с ударными взаимодействиями / С.П. Горбиков // Математические заметки, – т.70. – №2. – 2001. – 14 с.
- Грунский И.С. Распознавание лабиринтов при помощи конечных автоматов / И.С. Грунский, Е.А. Татаринов // Труды 4 междунар. конф. «Параллельные вычисления и задачи управления», РАСО’2008, 27–29 октября 2008 г., Москва. – М: ИПУ РАН им. В. А. Трапезникова, 2008. – С. 1483–1498.
- Грунский И.С. Распознавание конечного графа блуждающим по нему агентом / И.С. Грунский, Е.А. Татаринов // Труды 6 междунар. конф. «Параллельные вычисления и задачи управления», РАСО’2009, 27–29 октября 2009 г., Москва. – М: ИПУ РАН им. В.А. Трапезникова, 2008. – С. 483–498.
- Грунский И.С. Об алгебре языков, представимых графами с отмеченными вершинами / И.С. Грунский, Е.А. Пряничникова // Труды Ин-та прикл. математики и механики НАН Украины. – 2009. – т.18. – С. 37–46.
- Грунский И.С. Эксперементы с помечеными графами / И. С. Грунский, С. В. Сапунов, Е.А. Татаринов // Восьмая международная научная конференция «Дискретные модели в теории управляющих систем» М: МГУ 2009. – С. 43–45.
- Москинова Г.И. Дискретная математика / Москинова Г. И. – М.: Логос, 2000. – 198 с.
- Олищук С.А. Базовые графы для построения топологии многопроцессорных систем / С.А. Олищук, М.А. Волк // Конференция «Системы управления, навигации и связи» – Харьков: ХНУР, 2010. – т.16, вып.4. – С.150–158.
- Пинчук. В.П. Базовые графы для построения топологии многопроцессорных систем / В.П. Пинчук // Труды 4 конф. «Искусственный интеллект» – Донецк: ГУИиИИ, 2004. – № 4. – С.46–58.
- Пришляк А.О. Топологическая эквивалентность векторных полей морса-смейла c beh-2 на трехмерных многообразиях / А.О.Пришляк // Успехи математической науки – т.56. – №2. – 2001. – С. 211–212.
- Пряничникова Е.А. О полноте системы аксиом для алгебры языков, представимых ориентированными графами с отмеченными вершинами / Е.А. Пряничникова // Вісник донецького національного університету. Сер. А: Природничі науки. – 2010. – №.1. – С. 259–267.
- Пряничникова Е.А. Характеризация языков, представимых в графах с отмеченными вершинами / Е.А. Пряничникова // Труды Ин-та прикл. математики и механики НАН Украины. – 2010. – т.19. – С. 37–46.
- Пряничникова Е.А. О полноте системы аксиом для алгебры языков, представимых ориентированными графами с отмеченными вершинами / Е.А. Пряничникова // Вісник донецького національного університету. Сер. А: Природничі науки. – 2010. – №.1. – С. 259–267.
- Пряничникова Е.А. Алгебра языков, представимых в отмеченных графах / Е.А. Пряничникова // Theoretical and Applied Aspects of Cybernetics: International Scientific Conference of Students and Young Scientists. – Kyiv. – 2011. – P. 177–179.
