Анотація

M. Wim , N. Silviu-Iulian Аналіз стабільності гідродинамічної моделі потоку для поведінки ТСР Ця стаття зосереджується на аналізі стабільності деяких класів нелінійних моделей із затримкою, з якими стикається гідродинамічна модель для мережі TCP/AQM. Об'єднуючи аналітичні і чисельні інструменти цих моделей, вивчається як і місцева, так і глобальна поведінка рішень. Серед інших, показана присутність хаотичного фактору , який безпосередньо підтримує пропозицію TCP, оскільки детермінований процес може викликати або сприяти хаотичній поведінці в мережі.

Головні цілі статті: по-перше забезпечувати якісну і кількісну інформацію відносно динаміки моделей, і по-друге, пояснити можливості обчислювальних інструментів для стабільності і аналізу роздвоєння вирівнювань диференціала затримки.

Ключові слова:

Системи з затримкою; контроль затору.

1 Введення

Аналіз гідродинамічної моделі потоку для опису швидкохідної поведінки мережі представляє цікаву тему, що повертається, до минулих років, переважно для простоти моделей, і для хорошої і легкої інтерпретації завдання зворотного зв'язку як контролю стандарту.

Недавно, в [Misra і інші., 2000; Hollot і інші., 2002; Kelly, 2001] були представлені деякі моделі, що описують поведінку переповнених роутерів в мережах TCP/ AQM. Як очікується, такий вигляд моделей описуються нелінійними диференціальними рівнянями із затримкою, де затримка представляє час операцій передачі в мережі.

Модель [Misra і інші., 2000; Hollot і інші., 2002; Kelly, 2001] включає такі поєднанні нелінійних диференціальних рівнянь з затримкою, яка змінюється з часом:

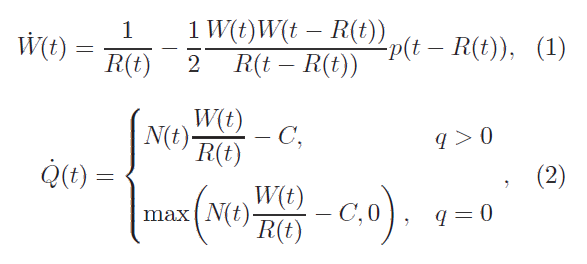
де W(t) позначає середній розмір вікна TCP [пакети], Q(t) - середня довжина черги [пакети], R(t) - RTT [секунди], C – пропускна спроможність каналу [пакет/с], N(t) - кількість TCP сесій p(t) - ймовірнісна функція маркірування пакету .

Довжина черги Q(t) і розмір вікна W(t) є позитивними. Ймовірнісна функція маркірування пакету p(t) приймає значення лише у [0, 1]. RTT може бути представлена як

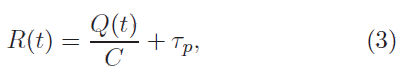
де tp-затримка розповсюдження [с].

Перше диференціальне рівняння описує динамічне керування вікна TCP. Перший елемент 1/Ri описує у вікні адитивне збільшення фази і другий елемент W (t)/2 мультиплікативне зменшення фази (в тому числі ймовірнісна функція маркірування пакету).

2. Розробити реалізацію математичної гідродинамічної моделі для обраних противоперевантажних алгоритмів та провести моделювання роботи цих алгоритмів при різних вхідних параметрах. Рівняння (2) описує довжину черги вузьким місцем, як різниця між швидкістю прибуття пакету NW/R і пропускною спроможністю C, припускаючи, що там є немає внутрішньої динаміки в вузькому місці (грубо кажучи, простих інтеграторів).

За допомогою гідродинамічної моделі потоку, як (1)–(3), активне керування чергою можна інтерпретувати як зворотній зв'язок проблеми контролю, де дія контролю складається з маркування пакетів (з ймовірністю p) в залежності від довжини виміряної черги Q.

Кількість TCP сесій N(t) і RTT R(t) постійні, тобто N(t) = N і R(t) = R. Пізніше це може бути гарним наближення, коли в RTT переважає затримка розповсюдження. Це відбувається, коли пропускною спроможністю C велика. Також врахуємо, що ймовірнісна функція маркірування пакету p(t) є пропорційна довжині черги, тобто p(t) = K q(t),рівняння (1) та (2) набувають вигляду:

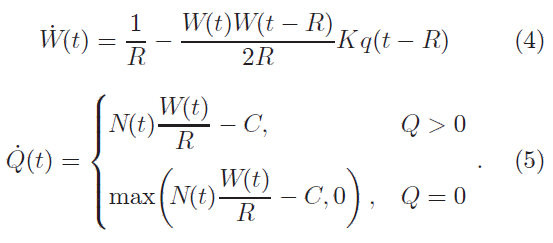
де Qmax – максимальне значення черги [пакети].

В унікальний точка рівноваги (4) і (5) надає:

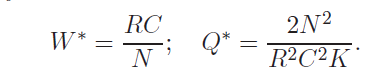
У гол. 5 з [Hollot співавт., 2002] лінеарізований аналіз стійкості точки рівноваги проводили в частотній області, де зміну часу обробки циклу було враховано, але деякі ефекти затримки розглядалися як висока ступінь невизначеності частоти. Посилання [Hollot & Chait, 2001; Melchor-Aguillar & Niculescu, 2003] містить аналіз стабільності рівноваги на основі формули Ляпунова. В ході додаткового спрощення рівняння (4) має вигляд

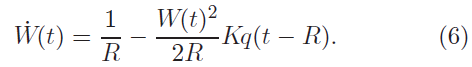
У роботі [Hollot & Chait, 2001] автори довели, що коли затримка дорівнює нулю у рівноважній точці системи, (6) і (5) асимптотично стабільні для всіх K> 0. Коли затримка відрізняється від нуля, підхід Ляпунова-Розуміхіна використовується, щоб показати асимптотичну стійкість точки рівноваги (6) при досить малих (K / N)> 0. У роботі [Melchor-Aguillar & Niculescu, 2003] цей результат був уточнений і достатні умови для параметрів забезпечення місцевої стійкості та оцінки області тяжіння були отримані за допомогою менш консервативного підходу Ляпунова-Красовського.

Структура роботи полягає в наступному: після опису перетворення місця і часу, ми повністю характеризуємо лінійні області стійкості стаціонарного рішення рівняння (4) - (5) як функцію параметрів моделі. Більш докладно, тільки один інтервал затримки гарантує асимптотичну стійкість лінеарізованної моделі. Потім беремо нелінійності до уваги і вивчати глобальний алгоритм прийняття рішень.

Трансформація

Коли час обробки циклу R важається постійним, можна застосувати перетворення місця і часу (4) - (5), що дає:

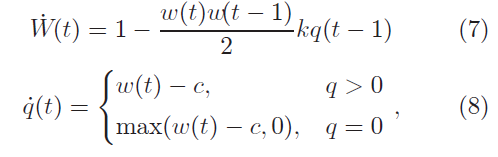
де

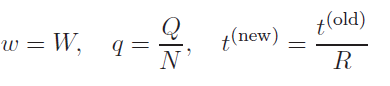
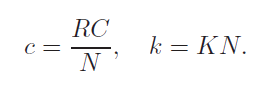
Важливість цього перетворення полягає в тому, що чотири модельних параметри (K, N, C, R) зводяться тільки до двох параметрів (k, c). Це полегшує дослідження залежності приймачів та властивості їх стабільності від параметрів системи.

Перелік посилань

1. Cooke, K. L. & Grossman, Z. [1982] “Discrete delay, distributed delay and stability switches,” J. Math. Anal. Appl. 86, 592–627.
2. Engelborghs, K., Luzyanina, T. & Samaey, G. [2001] “DDE-BIFTOOL v. 2.00: A Matlab package for bifurcation analysis of delay differential equation,” TW Report 330, Department of Computer Science, Katholieke Universiteit Leuven, Belgium.
3. Engelborghs, K., Luzyanina, T. & Roose, D. [2002] “Numerical bifurcation analysis of delay differential equations using DDE-BIFTOOL,” ACM Trans. Math. Softw. 28, 1–21.
4. Fall, K. & Varadhan, K. [2003] “The ns manual,” available from http://www-mash.cs.berkeley.edu/ns.
5. Hollot, C. V. & Chait, Y. [2001] “Nonlinear stability analysis for a class of TCP/AQM networks,” in Proc. 40th IEEE Conf. Decision and Control, ed. Zhu, J. J., pp. 2309–2314.
6. Hollot, C. V., Misra, V., Towsley, D. & Gong, W. B. [2002] “Analysis and design of controllers for AQM routers supporting TCP flows,” IEEE Trans. Autom. Contr. 47, 945–956.
7. Kelly, F. P. [2001] “Mathematical modelling of the internet,” in Mathematics Unlimited — 2001 and Beyond, eds. Engquist, B. & Schmid, W. (Springer-Verlag, Berlin), pp. 685–702.
8. Kolmanovskii, V. & Myshkis, A. [1992] Applied Theory of Functional Differential Equations (Kluwer Academic Publishers, Dordrecht).
9. Low, S., Paganini, F. & Doyle, J. C. [2002] “Internet congestion control,” IEEE Contr. Syst. Mag. 22, 28–43. Melchor-Aguillar, D. & Niculescu, S.-I. [2003] “Remarks on non-linear stability analysis for a class of TCP/ AQM networks,” in Proc. 4th IFAC Workshop on Time-Delay Systems.
10. Misra, V., Gong, W. B. & Towsley, D. [2000] “Fluid based analysis of a network of AQM routers supporting TCP flows with an application to RED,” in Proc. ACM/SIGCOMM’00. Niculescu, S.-I. [2001] Delay Effects on Stability: A Robust Control Approach, Lecture Notes in Control and Information Sciences, Vol. 269 (Springer-Verlag, Heidelberg).
11. Seydel, R. [1994] Practical Bifurcation and Stability Analysis: From Equilibrum to Chaos, Interdisciplinary Applied Mathematics, Vol. 5 (Springer, NY).
12. Tian, Y. & Gao, F. [1998] “Adaptive control of chaotic continuous-time systems with delay,” Physica D117, 1–12.
13. Veres, A. & Boda, M. [2000] “The chaotic nature of TCP-AQM congestion control,” in Proc. IEEE INFOCOM 2000.