Analysis of the cyclic properties of the automaton graph
Сontents
ExordiumComplex systems that interact with the environment may be exposed to the deforming effects of her. These effects can lead to changes in the structure of the system and, as a consequence, to change their behavior. In this regard, there are problems in analysis of system behavior, which have undergone such distorting influences. One of the basic mathematical models of the system is a model of a state machine. The above-mentioned problems of the analysis of behavior in the automaton model are studied in experiments with automata theory, technical diagnostics, synthesis theory of discrete systems, where they are key. 1. TopicalityIn particular, the task of analyzing the behavior becomes more and more important due to the widespread introduction of various microelectronic systems and components critical applications and increased requirements to achieve the necessary level of safety [1]. Many of these classes can be described as the result of generation of machines from a given class reference automaton by the operation of transfer arcs in its transition graph. For example, the class of locally generated automata [2], the classes of automata generated by the stuck—at faults in their circuit implementation, and others can be described in this way. In some cases, the system, the structure of which was subjected to distortions may be resistant to the distortive effects, keeping the same behavior. Thus, the problem arises of studying such structural changes in the behavior of the new system which does not change in comparison with the old. The formalization of the task can be carried out within the framework of the theory of automata. The system defined by a finite automaton, and structural changes — the transfer of arcs in this machine. The behavior of automata, which are generated from each other by means of rendition arcs, has been studied for a long time. Basically, this problem was considered in the framework of the experiments with machine guns [3]. In graph theory, is also considered related problems, which is regarded as the problem of determining when one of the graphs (automatic) can be obtained from the other by a sequence of arcs rendition [2]. In [4] it was shown that the transfer of exactly one arc in the above machine always causes a change in his behavior — the machine is not equivalent to the original machine. Later influence rendition of arcs on the behavior of the machine has been studied in [5, 6]. In this paper we continue the investigation of the properties of machines that allow transfer arcs while maintaining the behavior, in terms of the cyclic structure of their transition graphs. 2. Statement of the problemBasic definitions of automata theory can be found in [7]. Under automatic Mealy will be understood that a finite state machine, the output sequence of which is (unlike the Moore machine) depends on the machine and the input signals. This means that the graph of states each edge corresponds to a certain value (output symbol). At the top of the graph Mealy output signals are recorded, and the arcs of the graph is credited with the condition of transition from one state to another, as well as the incoming signals. At the top of the graph Mealy output signals are recorded, and the arcs of the graph is credited with the condition of transition from one state to another, as well as the incoming signals. Mealy can describe the five A = (S, X, Y, δ, λ), where S, X, Y — alphabets states of input and output symbols, respectively, and δ, λ – the transition and output. The functions δ and λ normally apply to a lot of X* all input words of finite length. For convenience, the set of states of the automaton itself and will be denoted by a single letter: A = (A, X, Y, δ, λ). Machine A will be considered as the set of edges Ea, where the arc — a quadruple (s, x, y, t), where s — the initial vertex, x—character input, y — output symbol, t — the end of the arc, if δ(s, x) = t, λ(s, x) = y. We say that an input-output word w = (p, q) is generated by a state of the automaton A if λ(a, p) = q. The two states a and b of the same machine A or two different machines, respectively, A and B, are equivalent if for any input word p∈X *, the equality λ(a, p) = λ′(b, p) where λ′ — the output function of the automaton A or B. With each state and the associated automaton mapping λa plurality of input words to a set of output, defined by the equation λa(p) = λ(a, p) for all p∈X*. An automaton is said to be reduced if all its conditions are pairwise equivalent. Below we consider machines A and B, in which the input and the output alphabet are the same, i.e. A = (A, X, Y, δ′, λ′) and B = (B, X, Y, δ′, λ′). In this case, as usual, the map φ : A → B is called a homomorphism of an automaton A is an automaton B, if for all a a∈ A and x∈>X: 1)φ(δ(a,x))=δ(φ(a)x). 2)λ(a,x)=λ′(φ(a)x). Let e = (a, x, y, b) — automatic arc A and e′(φ(a),x,yφ(b)) — arm automaton, i.e. homomorphism φ induces a mapping of the set of arcs in the set of edges EA EB. This map is also denoted φ and write φ(e)=e′. Doug e′ is called the image of the arc from the homomorphism f φ, and the arc e is called a prototype e′ on φ. The homomorphism φ is complete if every arc of a prototype in an arc of A. A full one–to–one homomorphism A to B is called an isomorphism machines A and B are isomorphic and denote A = B. In its structure, automatic – is a finite directed graph. Path machine – a sequence of arcs (a1, x1,y1, b1 ) (a2, x2,y2, b2 ) … (an, xn,yn, bn ), which arcs have a common neighboring incident vertices: a2=b1, a3=b2…an=bn-1, and each Arm occurs exactly one viewed. n is the number of edges of the path length. a1 condition called the beginning of the path, and bn – its end. Then it is said that the state bn reachable from a1. Path, each vertex of which belongs to no more than two of its arcs is called simple. Cycle (a simple cycle) is a path (easy way), in which the initial and final vertices are the same. Machine in which each pair of states reachable from each other, said to be strongly connected. A pair of states, each of which is accessible from the other, said one achievable. Relation of mutual reachability is an equivalence on the set of states. Classes relationship of mutual reachability called strongly connected components of the machine or strong components. Let A = (A, X, Y, δ, λ) — shown automatic, and e = (s, x′, y′, s1) — its arc. By switching the arc e, e.g., the state s2, other than s1, we mean the replacement of the arc to the arc (s, x′, y′, s2). Let the automaton A′ is derived from the automaton A redeployment of a set of arcs in the EA. The aim is to investigate the structure of the machine cycles and based on this determine the conditions under which the automaton A′ is isomorphic to the original automaton A. 3. Examples of transfer arcsRecall that the transfer of one arc always leads to non-isomorphic to the automaton. It is easy to give examples where the transfer of the two arcs in the machine also generates a new machine is not isomorphic to the original. In [4] were sufficient conditions for the preservation of the behavior of an automaton for the transfer of the two arcs, and it was shown that for any positive integer k > 1, there is a reduced automaton in which there is a subset of k arcs, the simultaneous transfer of which leads to an isomorphic machine. In [5] it was proved that the transfer of the two arcs of the input – output mark on these arcs are the same. There were also examples of not strongly connected automata, allowing transfer of multiple arcs, and it has been suggested that the state of being transferred arc which is not reachable from the states, where the movement is directed. In this paper, an example of rendition in a strongly connected machine that refutes this assumption. Here are some examples where transfer does not change the behavior of the original machine. Automaton A′(see Figure 1) is the result of transfer of the two arcs in the automaton A: arm (6, 0, 0, 8) being transferred to a state 9, and is replaced by the arc (6′, 0, 0, 9′), the arc (7, 0, 0, 9) is replaced by an arc (7′, 0, 0, 8′). It is easy to see the mapping φ: A → A′, wherein φ(1) = 1′; <φ(2) = 2′; φ(3) = 3′; φ(4) = 4′; φ(5) = 5′; φ(6) = 7′; φ(7) = 6′; φ(8) = 8′; φ(9) = 9′, is an isomorphism of the automaton A on machine A′. 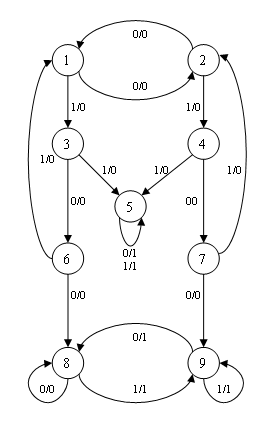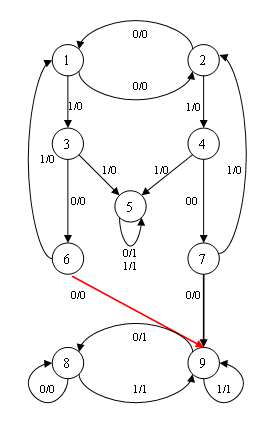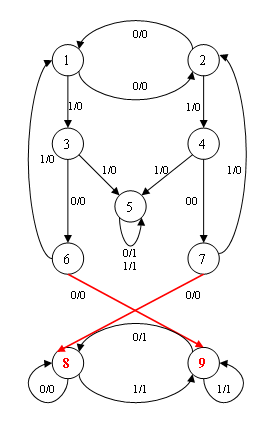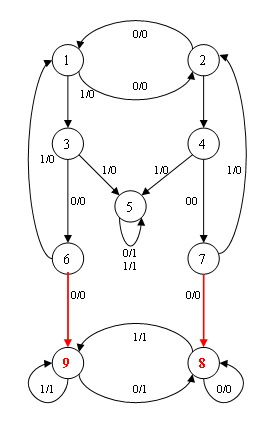
Figure – 1. Example isomorphism machines at the transfer of the two arcs In this example, the strongly connected components of the automaton A - is the set of states {1,2,3,4,6,7}, {5}, {8,9}, and throws the arc prilezhat different components. The following example (see Figure 2) shows the ferrying of arcs within a strong component because he automaton A is strongly connected. The automaton A′ is obtained by replacing the following arcs: (3, 1, 0, 5) to (3′, 1, 0, 6′), (4, 1, 0, 6) to (4′, 1, 0, 5′), (5, 1, 0, 1) to (5′, 1, 0, 2′), (6, 1, 0, 2) to (6′, 1, 0, 1′). It is easy to see that mapping φ: A → A′, wherein φ(1) = 2′; φ(2) = 1′; φ(3) = 4′; φ(4) = 3′; φ(5) = 5′; φ(6) = 6′ is an isomorphism of the automaton A on machine A′. 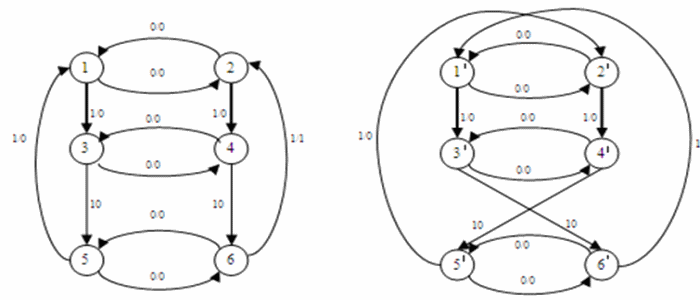
Figure – 2. Example isomorphism machines at the transfer of the four arcs in a strongly connected machine 4. Communication cyclic structure and the behavior of an automatonAnalysis of the cyclic properties of the machine allows the following conclusions. 1) Let A – standalone machine, ie its set of inputs consists of a single character: X = {x}. Transition graph of autonomous machine in general is a collection of connected components, each of which is a cycle with its member trees. Each state machine generates a stand–alone component that is either a cycle or a cycle with its affiliated «tail». For isomorphism necessary that a plurality of such components over all states in the machine before and after the transfer the same. This is possible only when being transferred arc belonging to the tail and the earlier «first» of the cycle. In this transfer should take place in such a state that produces exactly the same cyclic sequence as the «first» state of the cycle. But then A — unreduced machine comprising a pair of equivalent states, which contradicts the hypothesis. Thus, the analysis of the cyclic structure in a stand–alone machine allows us to prove that the transfer of one arch in the offline machine is not possible. It is easy to build a stand–alone machine, which can be flown, for example, the two arcs in the «tail» and get isomorphic machine. 2) Let A — non–autonomous machine. Stand–alone machines form Ai = (A, {xi}, Y, δi, λi) is said to be autonomous components of the automaton A. And then the machine can be set to specify its stand–alone component. The question is: how does transfer to the many self–contained component of the machine. The following example (see Figure 3) shows that this transfer is possible, which saves a lot of stand–alone component of the machine, but it leads to non–isomorphic to the automaton. 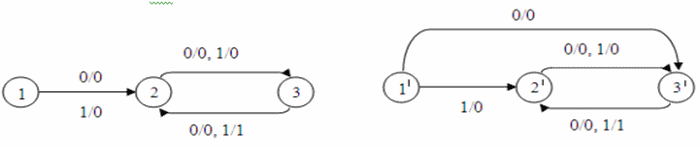
Figure – 3. Example storing a plurality of stand-alone component and violations of isomorphism automata transfer of one arc 1 in the automaton A has two equally directed arc (leading to state 2). A in the automaton A' such states one less. This implies a violation of isomorphism of A and A '. 3) The examples show that there are strongly connected machine transfer, preserving isomorphism, but have not been able to build a machine with two such redeployment. 5. Overview of resultsWe obtained the following results: 1. Analysis of the cyclic structure in the case of an autonomous automaton (in which |X| = 1) allowed to show that the transfer of one arc are not autonomous automaton (Example 3); 2. found examples of strongly connected automata, in which there are ≥4–rendition–preserving isomorphism (Example 2); 3. have not been able to build a automaton with two such redeployment; 4. shows that the transfer may be more than 2 arcs, at which the input–output mark on the different arcs of thrown (Example 2). FindingsThe results will continue to analyze the relationship between the cyclic structure of automaton and the preservation of its behavior in the transfer arcs. As the examples show, the transfer arcs preserving isomorphism, it is possible to machines that have a certain symmetry of the transition graph, which is also reflected in the cyclic structure of the graph. However, the example in Fig. 3 shows that only the combination of the analysis cycle in the automaton is not enough. Should be involved and other invariants of the transition graph. In writing this essay master's work is not yet complete. Final completion: January 2014. Full text of the work and materials on the topic can be obtained from the author or his manager after that date. Literature
|
