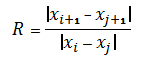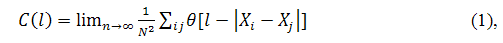Автор: Денисенко М.И., Беловодский В.Н.
Источник: Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС КМ - 2013) - 2013 / Матерiали IV мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. — Донецьк, ДонНТУ — 2013, Том 1.
Денисенко М.И., Беловодский В.Н. Определение размерности при реконструкции модели: подходы, методы, сравнительный анализ. Рассмотрены основные этапы реконструкции обыкновенных дифференциальных уравнений на базе временных рядов. Выполнено исследование и сравнительный анализ методов определения размерности модели.
В данной работе предполагается, что формирование математической модели будет проводится на базе временных рядов, получаемых с метеостанции Vantage Pro 2, установленной на факультете КНТ ДонНТУ. Данная метеостанция проводит определение ряда показателей (температуру, влажность воздуха, давление, скорость ветра) и передачу их на сервер. Все кафедры КСМ с помощью системы «АКИАМ». Интервал замеров составляет 10 минут. Таким образом, в процессе ее эксплуатации постоянно формируется и постепенно накапливается совокупность временных рядов. Наличие этой информации делает вполне реальной задачу разработки прогностического комплекса.
Процедуру получения модельных уравнений по временным рядам, которая достаточно часто обсуждается в научной литературе последнего десятилетия, называют реконструкцией уравнений.
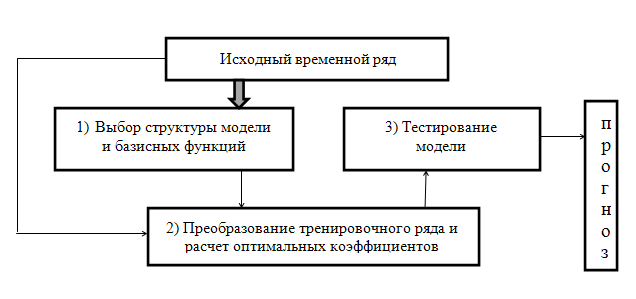
Рисунок 1 – Схема процесса моделирования по временному ряду.
Реконструкция дифференциальных уравнений проводится по схеме (рис.1). На первом этапе (1) на основании априорных данных, по оценке размерности множественной структурой модели: ослабляются шумы, с необходимой частотой выбираются точки, восстанавливаются дополнительные переменные и т.п. Далее, искомую функцию F представляют с помощью выбранных на первом этапе базисных функций с неизвестными коэффициентами и находят значения коэффициентов, которые обеспечивают наилучшее соответствие модели и экспериментальных данных. На третьем этапе результаты предсказания с помощью полученной модели сравниваются с данными тестовой части ряда. При этом оценивают качество получившейся модели, для чего используются критерии, определяемые целью моделирования. [1]
На кафедре КСМ в течение последних четырех лет выполнен ряд магистерских работ в этом направлении, в частности, выпускниками Гриценко А.В и Сивяковым А.С. была разработана программная система Fcomplex, предназначенная для краткосрочного прогнозирования метеопараметров по временным рядам с использованием конечных математических моделей. Прогнозирование в ней осуществляется на базе временных рядов, снимаемых с метеостанции Vantage Pro 2. Fcomplex - это программная система для составления краткосрочных прогнозов значений метеопараметров "Температура", "Давление", "Влажность" и "Скорость ветра". Для определения размерности модели в ней используются методы – главных компонент и ложных соседей, а для построения аппроксимирующих зависимостей, – искусственные нейронные сети и метод Эглайса. [5]
В данной работе расчет прогноза предполагается проводить по традиционной схеме путем выполнения следующих этапов:
1. получение временного ряда из базы данных (БД), содержащей данные снимаемые с метеостанции Vantage Pro 2;
2. анализ данных;
3. определение размерности модели;
4. прогнозирование;
5. проверка эффективности модели.
В данной работе хотелось бы остановиться на третьем из перечисленных этапов, так как он является одним из важнейших при реконструкции уравнений.
Выбор размерности модели D можно осуществлять на основе предварительного анализа временного ряда. В литературе описаны различные подходы к решению этой задачи. Рассмотрим некоторые из них, которые можно отнести к числу основных. Это метод Брумхеда-Кинга, оценка корреляционной размерности методом Грассбергера-Прокаччиа и метод ложных ближайших соседей.
Идея метода Брумхеда-Кинга состоит в следующем. Сначала по скалярному ряду восстанавливаются методом задержек векторы w(ti) в пространстве вложения достаточно большой размерности. Затем в этом пространстве производится преобразование поворота, причем направления новых осей координат выбираются в соответствии с теми направлениями, вдоль которых наиболее интенсивно развивается движение. Оценкой сверху для размерности служит количество направлений, вдоль которых имеется существенная протяженность траектории. Составляющие векторов вдоль тех направлений, которые слабо «осваиваются траекторией» списываются на влияние шума и ими пренебрегают. [1]
Метод ложных соседей основан на проверке того свойства, что фазовая траектория, восстановленная в пространстве достаточной размерности не должна иметь самопересечений. При пробной размерности D для каждого восстановленного вектора xk отыскивают одного (самого близкого) соседа; увеличив D на 1, определяют, какие из соседей оказались ложными (сильно разошлись), а какие – истинными. Подсчитывают отношение числа ложных соседей к общему числу восстановленных векторов. Если при увеличении D это число становится малым при некотором значении D*, то последнее и есть оценка размерности пространства, в котором достигается вложение траектории моделируемого движения [2].
Приведём один из алгоритмов вычисления относительного количества ложных ближайших соседей в восстановленном аттракторе. В лаговом пространстве выбираются две соседние точки, принадлежащие восстановленному аттрактору - хi и хj, вычисляется расстояние между ними, а также расстояние между следующими двумя точками - хi+1 и хj+1. Далее, определяется соотношение между этими расстояниями:
Поскольку мы имеем дело, как правило, с гладкими процессами, то после одной итерации точки сильно не разбегутся даже при больших значениях показателя Ляпунова ?. Поэтому если полученная величина превышает некоторое пороговое значение (обычно - 10), то точки хi и хj можно считать ложными соседями. Таким образом, в идеальном случае, минимально необходимой будет такая размерность лагового пространства, при которой число ложных соседей равно 0 [4].
Метод Грассбергера–Прокаччиа заключается в восстановлении аттрактора, «похожего» на исходный, последовательным сдвигом на величину ?. Для оценки размерности вложения последовательно получают новые размерности и измеряют некоторую характеристику получившегося многомерного ряда. После некоторого значения эта величина обычно перестает увеличиваться, что говорит о достижении размерности вложения. В качестве такой характеристики в нашем случае используется корреляционный интеграл C(?). Корреляционный интеграл (корреляционный показатель) – это вероятность того, что временной ряд содержит пару точек, расстояние между которыми не превышает ?.
Метод заключается в построении зависимости корреляционного интеграла от характеристического расстояния:
где l - характеристическое расстояние, ? - функция Хэвисайда, Xi и Xj точки d-мерного фазового пространства, N - количество экспериментально полученных точек фазовой траектории. Зависимость (1) может быть выражена как
где Dс корреляционная размерность исследуемого аттрактора. Как известно, для простых объектов, таких как линия или плоскость, корреляционная размерность будет равна размерности объекта. При увеличении размерности фазового пространства корреляционная размерность растет, выходя при определенном значении в насыщение. Уровень насыщения является фрактальной размерностью, а значение размерности фазового пространства - минимальной размерностью вложения аттрактора. [3].
Чаще всего для определения размерности модели при реконструкции уравнений используется метод Грассбергера-Прокаччиа, который является одним из наиболее распространенных для определения корреляционной размерности. Его использование позволяет анализировать исходный ряд, поместив его в n-мерное пространство, что дает основания для получения более точных данных. Кроме того, программная система Fcomplex составлялась на основе методов главных компонент и метода ложных соседей, поэтому для дальнейших исследований будет использован метод Грассбергера-Прокаччиа.
В работе описаны основные этапы реконструкции дифференциальных уравнений на базе временных рядов и методы определения размерности формируемой модели. В настоящее время результаты этого анализа уже используются при проектировании прогностической системы.
3. Исследователь. [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://ligis.ru/effects/stat/modules/sttimser.html – Анализ временных рядов.
4. M. B. Kennel, R. Brown, and H. D. I. Abarbanel. Determining embedding dimension for phasespace reconstruction using a geometrical construction// Phys. Rev. A, 45, 3403, 1992.
5. Гриценко А.В. Реконструкция уравнений и прогнозирование метеопараметров по их временным рядам. [Текст] – Донецк, ДонНТУ, 2010. – 149 с.