Сравнение алгоритмов планирования распределения задач для однородных распределенных вычислительных систем

Автор: Н.В. Морев 

 Аннотация

Проводится экспериментальное сравнение эффективности различных эвристик для решения NP-полной [1] задачи распределения подзадач в однородной распределенной вычислительной системе. Показатель, взятый за основу при сравнении – длина плана. Исследуется влияние характеристик исходного графа задач и вычислительной системы на эффективность алгоритмов. В качестве базовых характеристик использовано число вершин, число связей и число процессоров.

Введение

В наши дни создание высокопроизводительных вычислительных систем немыслимо без использования распределенных вычислительных ресурсов и параллельного выполнения множества задач. При этом разработчики алгоритмов планирования сталкиваются с рядом требований: обеспечение надежности вычислений, обеспечение приоритезации задач, обеспечение заданных уровней обслуживания и т.д. [2] В статье рассматривается проблема оптимизации распределения задач по узлам по критерию минимального общего времени выполнения всех задач. Сложность этой задачи связана с реализацией двух противоречащих требований: 1) необходимо как можно активнее использовать возможности параллелизма, 2) необходимо как можно сильнее снизить накладные расходы на пересылку данных между процессорами, на которых выполняются задачи. Так как рассматриваемая задача является NP-полной [3], то для ее решения на практике применяются различные эвристики, позволяющие за полиномиальное время получить результат близкий к оптимальному. Можно выделить несколько классов алгоритмов планирования по используемым подходам: списочное планирование, кластеризация, генетические алгоритмы [3], имитация отжига [4] и др. В статье рассматриваются алгоритмы, относящиеся к первым двум классам, с целью анализа эффективности их применения.

Постановка задачи

Используется модель, основанная на представлении приложения в виде ациклического ориентированного графа задач G=(V, E, w, c), где V – множество вершин-задач, E – связи между задачами, обозначающие какую-либо зависимость (например, зависимость по данным), влияющую на порядок выполнения, w – множество весов задач, условно обозначающих вычислительную сложность каждой задачи в виде времени, которое требуется на ее выполнение, c – множество весов связей между задачами, обозначающих накладные расходы, связанные с пересылкой информации между программными модулями, которые, выполняются на разных процессорах. Если задачи выполняются на одном процессоре, то вес связи принимают равным 0. Целевую распределенную вычислительную систему представляют в виде множества вычислительных узлов P. Время в задаче задается дискретно, т.е. каждый момент времени может быть обозначен числом из множества Q₀⁺ целых положительных чисел, включая 0. Считается, что: 1) каждый процессор в каждый момент времени может обрабатывать не более одной задачи, 2) пересылка информации между процессорами производится асинхронно с процессом вычисления и не влияет на него. Таким образом, учитывая вышеперечисленные условия, задачу можно отнести к типу P|prec|Cmax по предложенной в [5] классификации, т. е. к задачам минимизации длины плана с заданными ограничениями порядка выполнения задач на конечном множестве процессоров.

Задача планирования заключается в том, чтобы отобразить множество задач на множество процессоров и определить порядок выполнения задач на каждом из процессоров. Результатом планирования является план, заданный как пара отображений (ts, proc), где ts:V-> Q₀⁺ – функция времени начала выполнения вершин V, а proc: V->P - функция размещения вершин V на множестве P. Таким образом, план описывает временное и пространственное размещение задач.

Длину плана S задают как

 где tf(n) = ts(n) + w(n) — время окончания выполнения задачи.

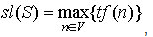
Исходя из свойств исходного графа задач и вычислительной системы, выполнимый план должен удовлетворять двум условиям. Необходимо удостовериться, чтобы ни на одном процессоре в ходе выполнения не оказалось одновременно более одной задачи. Для двух любых вершин n_i, n_j = V

 где ts(n, p) – время начала выполнения задачи на процессоре, tf(e_ij, p_i, p_j) – время окончания пересылки данных от задачи n_i к задаче n_j с заданными процессорными размещениями p_i, p_j.

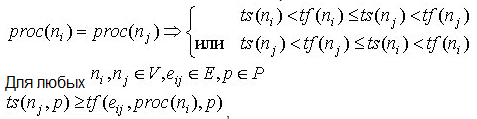
План, удовлетворяющий обоим условиям, называется выполнимым.

Очевидно, что для большинства встречающихся на практике графов задач и вычислительных систем, существует более одного выполнимого плана. Задача поиска оптимального плана состоит в том, чтобы минимизировать общее время выполнения (длину плана).

Реализация алгоритмов

Для сравнения в среде Matlab были реализованы 9 алгоритмов планирования, перечисленные в табл. 1, где P, V, E – обозначают соответственно число процессоров целевой вычислительной системы, число задач и число связей между ними. Пять из них относятся к классу алгоритмов списочного планирования, три – к классу алгоритмов кластеризации [3]. Отдельно рассматривается оптимальный алгоритм, т. к. в силу его большой вычислительной сложности, не представляется возможным исследовать его на той же области значений, что и предыдущие алгоритмы.

Таблица 1. Исследуемые алгоритмы планирования.

 Списочное планирование заключается в том, чтобы упорядочить вершины графа задач в список задач по какому-либо признаку и затем последовательно по одной задаче формировать план для данной задачи так, чтобы время начала ее выполнения было наименьшим. Порядок задач в списке определяется приоритетом задачи. В качестве приоритета может выступать топологический порядок задач в графе, верхний или нижний уровень вершины графа или их сумма (ВУ + НУ). Нижний уровень вершины в графе – это длина наибольшего пути в графе, начинающегося с данной вершины. Верхний уровень вершины – это длина наибольшего пути в графе, оканчивающегося данной вершиной. В алгоритмах со статическим приоритетом список вершин формируется один раз вначале выполнения алгоритма. В динамических алгоритмах следующая задача, подлежащая добавлению в план, вычисляется на каждой итерации.

Алгоритмы кластеризации задач направлены на минимизацию межпроцессорного взаимодействия за счет объединения сильно связанных между собой задач в кластеры, которые затем отображаются на процессоры заданной вычислительной системы. Здесь объектом рассмотрения на каждой итерации являются не вершины, а ребра графа задач. В алгоритме линейной кластеризации из графа задач сразу выделяют критический путь и формируют из него отдельный кластер, затем для всех оставшихся вершин итерация повторяется. В кластеризации по одному ребру на каждой итерации рассматривается одно ребро и определяется, приведет ли обнуление веса данного ребра к сокращению общей длины плана. Различия между алгоритмами кластеризации по одному ребру могут заключаться в определении порядка, в котором ведется рассмотрение ребер. Результат выполнения алгоритма кластеризации в общем случае еще не является искомым планом для задачи планирования, сначала получившиеся кластеры необходимо отобразить на процессоры целевой вычислительной системы.

Методология проведения эксперимента

Эксперимент проводится в системе Matlab версии 7.7.0. Графы задач генерируются случайным образом на основе равномерного распределения следующих характеристик графа: число вершин, число ребер.

Для каждого случайно сгенерированного графа задач выполняются все алгоритмы. Для каждого полученного плана проводится проверка его выполнимости.

Эффективность алгоритма для заданных исходных данных измеряется в виде длины получившегося плана и в виде соотношения длины плана к длине оптимального плана для выбранного графа там, где длина оптимального плана может быть вычислена.

Характеристики варьируются следующим образом. Число узлов: 1, 10, 100, 500, 1000. Число связей: 0, 1, 10, 100, 500, 1000 (но не больше (v²-v)/2, где v – число узлов). Число процессоров: 1, 2, 4, 10, 100, 1000 (но не больше числа задач). Выполнено по одному эксперименту для каждого алгоритма при всех указанных сочетаниях параметров.

Экспериментальные результаты

Зависимость от числа задач

 Рисунок 1. Зависимость длины плана от числа задач

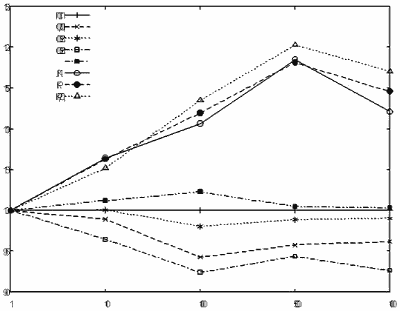
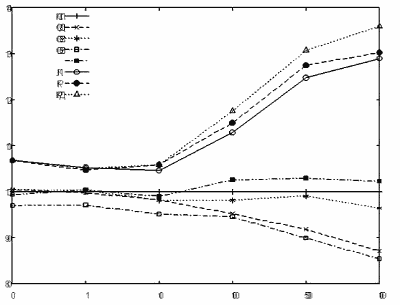
При сравнении зависимости длины плана от числа узлов в графе задачи, за основу для сравнения принят алгоритм ПСП. Результаты всех остальных алгоритмов показаны в процентном отношении к основному (рис. 1). При фиксированном числе узлов взято усредненное значение результата выполнения алгоритмов.

В вырожденном случае задачи с одной вершиной имеется единственное очевидное и оптимальное решение, поэтому все алгоритмы дают одинаковый результат и все графики выходят из одной точки. Из анализа графика сразу можно отметить, что с увеличением числа задач, алгоритмы разделяются на две обособленные группы с различными свойствами. Относительная длина плана, полученного с помощью кластерных алгоритмов растет, а у списочных алгоритмов уменьшается или остается в пределах 10% от базового результата.

Рост длины плана кластерных алгоритмов связан с тем, что при увеличении числа задач, увеличивается и число кластеров, которые затем необходимо разместить на процессоры вычислительной системы. Если процессоров меньше, чем кластеров, общая длина плана значительно увеличивается (в отдельных опытах в 2,5 раза по сравнению с алгоритмом ПСП).

Результаты алгоритмов списочного планирования слабо зависят от числа задач в графе. Начиная со 100 узлов их графики выходят на относительно стабильный уровень. Малые отклонения от базового показателя на числе узлов меньшем 100 объясняются меньшим числом проведенных опытов, а также тем, что для такого малого числа узлов случайно сгенерированные графы слабее отличаются друг от друга, чем при большом числе узлов.

Зависимость от числа связей

При сравнении зависимости длины плана от числа ребер в графе задачи, за основу для сравнения принят алгоритм ПСП (рис. 2). Результаты всех остальных алгоритмов показаны в процентном отношении к основному. При фиксированном числе ребер взято усредненное значение результата выполнения алгоритмов.

 Рисунок 2. Зависимость длины плана от числа связей

Из анализа графиков можно заключить, что при достаточно малом числе ребер в графе задач, все алгоритмы показывают слабо отличающуюся от базового алгоритма эффективность. Это связано с тем, что при практически полном отсутствии зависимостей задача упрощается за счет исключения одного из двух противоречащих друг другу требований – требования минимизации затрат на пересылку информации между процессорами.

Алгоритмы кластеризации пытаются минимизировать длину плана за счет

уменьшения связей между кластерами задач, однако, с ростом числа связей в графе, делать это становится сложнее, поэтому длина плана увеличивается.

 Рисунок 3. Зависимость длины плана от числа процессоров

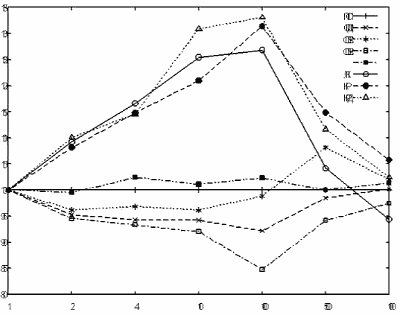
Среди алгоритмов списочного планирования наилучшие результаты показывают алгоритмы СПДП и СПСНУ. Алгоритм СПСНУ достигает этого за счет выбора в качестве наиболее приоритетных для планирования тех задач, которые относятся к критическому пути графа. Алгоритм СПДП достигает примерно того же результата путем последовательного перебора всех вершин графа и выбора из них наиболее приоритетной для планирования, что увеличивает сложность алгоритма на фактор равный числу узлов в графе и делает его непригодным для практического использования при достаточно большом числе узлов по сравнению с остальными алгоритмами.

Зависимость от числа процессоров

При сравнении зависимости длины плана от числа процессоров в целевой вычислительной за основу для сравнения принят алгоритм ПСП. Результаты всех остальных алгоритмов показаны в процентном отношении к основному (рис. 3). При фиксированном числе процессоров взято усредненное значение результата выполнения алгоритмов.

Анализ полученного графика показывает, что при увеличении числа процессоров целевой вычислительной системы эффективность всех алгоритмов становится примерно одинаковой. Это связано с тем, что с увеличением числа процессоров уменьшается и число проведенных опытов. Кроме того, число задач становится равным или близким к числу процессоров, т.е. практически неограниченным, что значительно упрощает этап отображения задач на процессоры для всех алгоритмов. Для алгоритмов кластеризации это также помогает исключить этап отображения кластеров на процессоры, что положительно влияет на эффективность этих алгоритмов.

Общее сравнение алгоритмов

Общее сравнение рассматриваемых алгоритмов проводилось по усредненным результатам всех проведенных экспериментов. Результаты работы алгоритма ПСП были взяты за основу для сравнения. Рисунок 4 показывает разницу в длине планов, получившихся в результате работы различных алгоритмов.

Выводы

В целом алгоритмы кластеризации показали худшие результаты, чем алгоритмы списочного планирования. Однако, из анализа зависимости от числа процессоров видно, что их эффективность увеличивается с ростом числа процессоров. Это связано с тем, что эти алгоритмы рассчитаны на среду с неограниченным числом процессоров и поэтому требуют дополнительного этапа приведения результата к вычислительной системе с заданным числом процессоров, на котором ухудшается конечный результат.

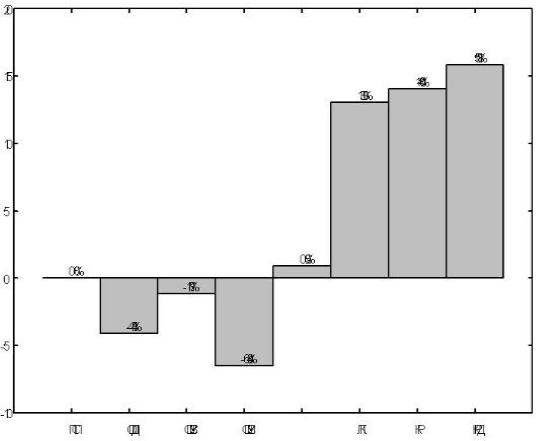
Рисунок 4. Сравнение по результатам всех экспериментов

Алгоритмы списочного планирования показывают примерно одинаковую эффективность. Даже алгоритм СПДП, имеющий большую вычислительную сложность по сравнению с остальными, не дает значительного выигрыша. Среди алгоритмов списочного планирования наилучшие результаты показывает алгоритм с приоритетом узлов по значению нижнего уровня.

Среди алгоритмов кластеризации наилучшую эффективность показала стратегия алгоритма ЛК - выделение критического пути в графе задач и отнесение всех его задач к отдельному процессору.

Список литературы

1. Томас Х. Кормен и др. Глава 34. NP-полнота // Алгоритмы: построение и анализ. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296.
2. Морев, Н. В. Планирование в грид-системах с неопределенными параметрами узлов. // Физика и радиотехника в медицине и экологии: Доклады 8-й межд. научн.-техн. конф. «ФРЭМЭ-2008». Книга 1. / ВлГУ – Владимир: 2008. – с. 302-305.
3. Sinnen, O. Task Scheduling for Parallel Systems. John Wiley & Sons – Hoboken, New Jersey, USA: 2007.
4. Калашников А. В., Костенко В. А. Параллельный алгоритм имитации отжига для построения многопроцессорных расписаний // Известия РАН. Теория и системы управления, 2008, №3, С. 101-110.
5. Graham R.L., Lawler E.L., Lenstra J.K. et al. Optimization and approximation in deterministic sequencing and scheduling: a survey // Ann. Discrete Math. 1979. № 5. P. 287–326.