Аннотация
Рассматриваются три метода выделения краев на цифровых изображениях: Собеля, Лапласа и математической морфологии. Результаты проведенных численных экспери- ментов позволили установить достоинства и недостатки применения указанных мето- дов в обработке цифровых изображений.
Ключевые слова: цифровое изображение, выделение краев.
Введение
Выделение краев играет важную роль в анализе изображений и распознавании обра- зов при решении проблемы компьютерного зрения. Края являются точками перепада зна- чений яркости в полутоновом изображении и поэтому важными характеристиками изо- бражения. Эти резкие точки перехода указывают местоположения контуров объектов на изображениях. Представление краев объектов на изображении позволяет уменьшить ко- личество данных, сохраняющих важную информацию о форме объектов в сцене. Выделе- ние краев является наиболее используемой технологий в процессе обработки цифрового изображения. При определении границ объекта производится вычисление двумерного пространственного градиента на изображении и выявляются области, соответствующие краям. При этом происходит оценка модуля градиента в каждой точке полутонового изо- бражения [1].
Выделение краев – термин в теории обработки изображения и компьютерного зрения, частично из области поиска объектов и выделения объектов, основывается на алгоритмах, которые выделяют точки цифрового изображения, в которых резко изменяется яркость или есть другие виды неоднородностей. Результатом выделения границ является набор связанных кривых, обозначающих границы объектов, граней и оттисков на поверхности, а также кривые, которые отображают изменения положения поверхностей. Объекты состоят из многочисленных частей различных цветных уровней. Перепад яркости – это связное множество пикселей, лежащих на границе между двумя областями (рис. 1) [1].
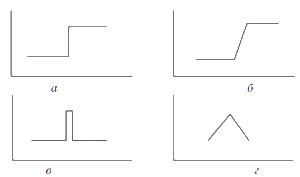
Рис. 1. Типы краев: а – край шага; б – край ската; в – край линии; г – край крыши
Край в изображении – это существенное местное изменение в интенсивности изображения, обычно связываемое с неоднородностью в интенсивности изображения. Как правило, указанное изменение описывается первой производной, характеризующей величину градиента. Предполагаемое расположение границы объекта на изображении обычно является перпендикуляром к вектору градиента.
Неоднородности в интенсивности изображения могут быть различного вида: краем шага, где интенсивность изображения резко изменяется от одного значения до другого, или краем линии, где интенсивность изображения резко изменяет значение, а затем быстро возвращается к начальному значению. Однако края типа шага и линии редко бывают в реальном изображении из-за того, что в сигнале превалируют низкочастотные компоненты вследствие сглаживания видеодатчиком. В результате край шага становится краем ската, а край линии – краем крыши, где изменения интенсивности не мгновенны и происходят в ограниченном интервале.
Этапы выделения краев
Выделение краев происходит за 3 этапа: фильтрация, улучшение и выделение.
Фильтрация. Первым шагом является фильтрация шума в исходном изображении. Случайные изменения значения интенсивности на изображении называются шумом. Наи- более распространенными типами шума являются: соль и перец, импульсный шум и га- уссовский шум. Алгоритмы шумоподавления обычно специализируются на подавлении одного конкретного вида шума. Не существует пока универсальных фильтров, детекти- рующих и подавляющих все виды шумов.
Улучшение. Чтобы облегчить обнаружение края, важно определить изменения в ин- тенсивности в соседней точке. Улучшение подчеркивают пиксели, которые имеют суще- ственное изменение значения интенсивности. Обычно на этом этапе происходит вычисле- ние градиента для пикселей изображения.
Выделение. У многих точек изображения имеются значения градиента, отличные от нуля, и не все эти точки являются краями. Поэтому должны использоваться некоторые методы, чтобы определить, какие точки являются краями.
Классические методы выделения краев
Для выделения краев на цифровых изображениях использованы классические методы Собеля и Лапласа [2].
Метод Собеля
Идея этого метода основана в наложении на каждую точку изображения двух масок вращения. Эти маски представляют собой две ортогональные матрицы размерностью 3x3 (рис. 2).
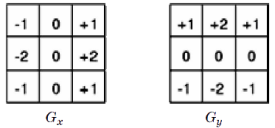
Рис. 2. Маски Собеля
Эти маски выявляют границы, расположенные вертикально и горизонтально на изображении. При раздельном наложении этих масок на изображение можно получить оценку градиента по каждому из направлений Gx, Gv. Конечное значение градиента определяется по формуле
Метод Лапласа
В методе Лапласа осуществляется умножение каждого элемента двумерной апертуры 3x3 на соответствующий элемент так называемой матрицы Лапласа (рис. 3):

Рис. 3. Матрицы Лапласа
Выделение краев на основе применения математической морфологии
Математическая морфология предназначена для исследования структуры некоторых множеств однотипных объектов. Любое изображение в компьютерной графике также обычно представляется в виде набора пикселей, поэтому операции математической мор- фологии могут быть применены и к изображению – для исследования некоторых свойств его формы и структуры, а также для его обработки [3].
Базовые операции
Перенос (translation) множества пикселей S на вектор b определяется как Sb=⟨S+b:s∈S.
Перенос t может быть определен как упорядоченная пара чисел ( δx,δy) , где δx – движение вдоль оси X, а δy – движение вдоль оси Y.
Расширение (Dilation) двоичного изображения B на структурный элемент S записыва- ется в виде B ⊕ S и определяется как

Сужение (Erosion) двоичного изображения B на структурный элемент S записывается как B – S и определяется как B-S={b|b+s∈B∀s∈S}
Сужение и расширение инвариантны относительно переноса:

Сравнение результатов применения различных методов выделения краев
Итогом исследования явилось создание приложения средствами C#, реализующего методы выделения краев. Это приложение обрабатывает файлы формата *.gif размером 256x256 пикселей. На рис. 4, 5 представлены результаты численных экспериментов по обработке изображений, а в таблице – их сравнение.

Рис. 4. Исходное изображение «House» – а; б – результат выделения краев методом Собеля; в – результат выделения краев методом Лапласа; г – результат выделения краев методом математической морфологии

Рис. 5. Исходное изображение «CameraMan» – а; б – результат выделения краев методом Собеля; в – результат выделения краев методом Лапласа; г – результат выделения краев методом математической морфологии
| Время | выполнения | , с | |
| Исходное изображение | Собеля | Лапласа | Математическая морфология |
| "House" | 2,57 | 1,12 | |
| "CamersMan" | 1,77 | 1,9 | 0,84 |
Заключение
Таким образом, в данной работе проведен анализ трех методов выделения краев: Со- беля, Лапласа и математической морфологии. Сравнение результатов обработки изобра- жений указанными алгоритмами показало, что метод на основе применения математиче- ской морфологии работает быстрее, чем остальные методы. Следует отметить, что наиболее четкие границы объектов на изображении получаются при обработке на основе применения оператора Собеля.
Список использованной литературы
- Senthilkumaran N. A. Study on Edge Detection Methods for Image Segmentation // N. Senthilkumaran, R. Rajesh // Proceedings of the International Conference on Mathematics and Computer Science (ICMCS-2009). – 2009. – Vol. 1. – P. 255–259.
- Гонсалес Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс. – М.: Тех- носфера, 2005. – 1070 с.
- Huang C.P. An Integrated Edge Detection Method Using Mathematical Morphology / C.P. Huang, R.Z. Wang // Pattern Recognition and Image Analysis. – 2006. – Vol. 16, № 3. – P. 406–412.