Аннотация
В работе показана возможность построения высокоэффективных вейвлет – преобразований ортогональными вейвлет – фильтрами Добеши по алгоритму Малла на базе свертки, вычисленной в системе остаточных классов.
Ключевые слова: вейвлет – преобразование, вейвлет – фильтр, вейвлет – функция, алгоритм Малла, свертка, цифровая обработка сигналов, система остаточных классов.
В настоящее время вейвлет – преобразование широко применяется в задачах обработки и кодирования сигналов и изображений самой различной природы (речь, спутниковые изображения, рентгенограммы внутренних органов и др.), распознавания образов, при изучении свойств поверхностей кристаллов и нанообъектов и во многих других случаях.
Появление в 1988 году ортогональных вейвлет-фильтров Добеши или так называемых фильтров с компактным носителем в значительной мере усилило интерес к вейвлет-анализу, т.к. открылись новые возможности не только для теоретического, но и для практического применения вейвлет-преобразования.
Важно отметить то, что вейвлет-фильтры Добеши строятся, исходя из критерия длины фильтров и, следовательно, являются фильтрами с конечным числом коэффициентов [1]. Вейвлет-функции Ψ(t) фильтров Добеши принято обозначать литерой D с добавлением цифры, соответствующей длине вейвлет-фильтра Добеши, т.е. D2, D4, D6 и т.д.
Пусть даны два фильтра h и g с ненулевыми элементами [2]:
 |
(1) |
Отметим соотношения между коэффициентами этих фильтров [2]:
h0+h1+h2+h3=1;
g0+g1+g2+g3=0;
g0=h3, g1=-h2, g2=h1, g3=-h0; (2)
h0+h2=h1+h3=0,5, 2h2=h1+3h3.
Найдём передаточные функции H(z) и G(z) в z -представлении:H(z)=h0+h1z+h2z2+h3z3; (3)
G(z)=g0+g1z+g2z2+g3z3=h0-h1z+h2z2-h3z3=-z3(-h3z-3+h2z-2-h1z-1+h0)=-z3H(-z1). (4)
Таким образом, мы получили
G(z)=-z3H(-z-1) (5)
Для восстановления сигнала требуются дополнительные фильтры H¯(z) и G¯(z) . Определим их как сопряжённые квадратурные фильтры по формулам:
H¯(z)=H(z-1), G¯(z)=G(z-1)=-z-3H(-z) (6)
Тогда второе соотношение H¯(z)H(-z)+G¯(z)G(-z)=0 из (3-4) выполняется. Первое соотношение H¯(z)H(z)+G¯(z)G(z)=1 принимает вид:
H(z-1)H(z)+G(z-1)G(z)=1 (7)
Вернёмся к частотной переменной z=e-iω . Поскольку коэффициенты {hn} – вещественные, то H(z-i)=H¯(ω). Поэтому последнее соотношение принимает вид |H(ω)|2+|G(ω)|2=1.
Найдём коэффициенты фильтров восстановления H¯(z) и G¯(z) из их определения H¯(z)=H(z-1), G¯(z)=G(z-1):
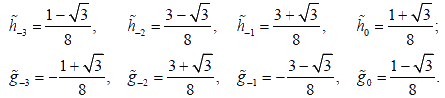 |
(8) |
Таким образом, метод одномерного дискретного вейвлет – преобразования (ДВП) N -го порядка последовательности nx определяется следующими рекуррентными соотношениями:
 |
(9) |
где an(i) и dn(i) являются аппроксимирующими и детализирующими коэффициентами i-го уровня, а gk и hk (k=0,1,...,N-1) – коэффициенты низкочастотного и высокочастотного анализирующих фильтров, соответственно.
С другой стороны, сигнал xn может быть восстановлен по коэффициентам {an(J),dn(J),...,dn(1)} путём последовательной итерации по формулам:
 |
(10) |
где g¯k и h¯k являются коэффициентами низкочастотного и высокочастотного синтезирующих фильтров, соответственно.
Для того, чтобы восстановленный сигнал соответствовал исходному, должны быть соответствующим образом подобраны анализирующий (раскладывающий) и синтезирующий (собирающий) фильтры.
Для вейвлет-преобразования функции f(x) необходимо вычислить серию коэффициентов {an,dn,dn-1,...,d1}, где an – аппроксимация функции, di – детазизирующие коэффициенты функции, i=1,...,n. Каждый коэффициент находится интегрированием (11, 12):
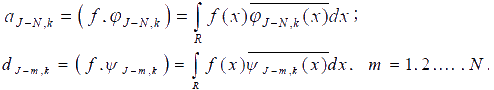 |
(11,12) |
Возникает проблема вычисления большого количества интегралов с необхо- димой точностью. Следует также учитывать, что при высоком уровне разрешения J носители функций, φJ,k(x) и, ψJ,k(x) становятся малыми порядка 2-J.
Быстрое вейвлет-преобразование, предложенное Мала позволяет решить эту проблему. Алгоритм Малла даёт возможность вычислять коэффициенты вейвлет- разложения без интегрирования, используя алгебраические операции на основе свёртки:
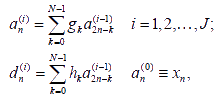 |
(13) |
где an(i) и dn(i) являются аппроксимирующими и детализирующими коэффициентами i-го уровня, а gk и hk (k=0,1,...,N-1) – коэффициенты низкочастотного и высокочастотного анализирующих фильтров, соответственно; xn – исходный сигнал; N – порядок фильтра.
Эти равенства обеспечивают быстрые алгоритмы вычисления вейвлет- коэффициентов (каскадные алгоритмы, алгоритмы Малла). Термин «быстрые» означает не только, что в (13) используются более быстрые алгебраические процедуры, но и то, что при каждом преобразовании общее число новых коэффициентов не увеличивается в два раза, а остаётся прежним.
Схема разложения сигнала по алгоритму Малла приведена на рис. 1.
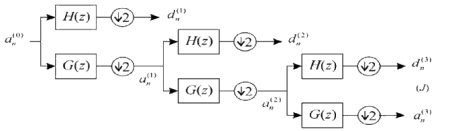
Рис. 1. Последовательность получения вейвлет-коэффициентов третьей октавы; H(z) и G(z), соответственно, высокочастотные и низкочастотные анализирующие фильтры в z -представлении
Единственное отличие фильтрации в алгоритме Малла от классического КИХфильтра, задаваемого уравнением
 [3], заключается в том, что значения фильтруемого ряда выбираются через один – индекс 2n-k в a2n-k(i-1). Это и есть
децимация 2↓ – исключение из обработки каждого второго элемента.
[3], заключается в том, что значения фильтруемого ряда выбираются через один – индекс 2n-k в a2n-k(i-1). Это и есть
децимация 2↓ – исключение из обработки каждого второго элемента.
Для двумерных сигналов – изображений – алгоритм разложения аналогичен тому, что применяется в одномерном случае (13). Пусть φ(x) – масштабирующая вейвлет-функция и ψ(x) – материнский вейвлет. Как известно, они порождают базисные функции φJ,n(x) и ψJ,n(x). Двумерный сигнал a(nq,n2) раскладывается по базисным в L2(R2) функциям φJ,n(x)φJ,m(y), φJ,n(x)ψJ,m(y), ψJ,n(x)φJ,m(y). Соответствующие коэффициенты принято называть следующим образом.
Аппроксимирующие коэффициенты a(J)(n1,n2) получаются как коэффициенты разложения по вейвлет-базису φJ,n(x)φJ,m(y). На рис. 2 (а) показано распределение пикселов после пошаговой обработки исходного изображения банком фильтров.
Горизонтальные детализирующие коэффициенты d2(J)(nq,n2) получаются как коэффициенты разложения по вейвлет-базису φJ,n(x)ψJ,m(y).
Вертикальные детализирующие коэффициенты d1(J)(nq,n2) получаются как коэффициенты разложения по вейвлет-базису ψJ,n(x)φJ,m(y).
Диагональные детализирующие коэффициенты d3(J)(nq,n2) получаются как коэффициенты разложения по вейвлет-базису ψJ,n(x)ψJ,m(y).
Схема разложения сигнала a0(n1,n2) изображена на рис. 2 (б).
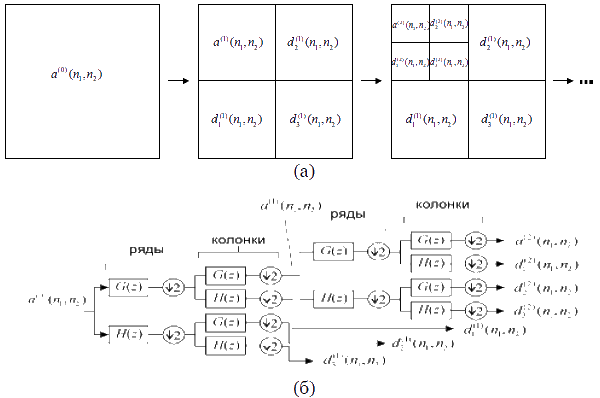
Рис. 2. Последовательность получения вейвлет-коэффициентов третьей октавы для двумерного сигнала: (а) –распределение пикселов после пошаговой обработки исходного изображения банком фильтров; (б) – в виде последовательности фильтров; H(z) и G(z), соответственно, высокочастотные и низкочастотные анализирующие фильтры в z -представлении
В аналитическом виде разложение двумерного сигнала фильтрами можно за- писать следующим образом:
 |
(14) |
В качестве собственно фильтров могут использоваться фильтры Добеши D4 четвёртого порядка. Вейвлеты Добеши являются вейвлетами с компактным носитeлем, что обеспечивает хорошие свойства приближения вейвлет-разложений. Они не имеют эксплицитного (явного) выражения, а задаются коэффициентами фильтрации. Анализирующие (разлагающие) высокочастотные (h) и низкочастотные (g) коэффициенты фильтра Добеши D4 задаются следующими коэффициентами [2]:
 |
(15) |
Графики вейвлетов Добеши D4 (db4) в среде MATLAB можно увидеть следующим образом (рис. 3):
[phi,psi,x]=wavefun('db4',10);
subplot(121); plot(x,phi);
title('y=\phi(x)'); axis square; grid on;
subplot(122); plot(x,psi);
title('y=\psi(x)'); axis square; grid on;
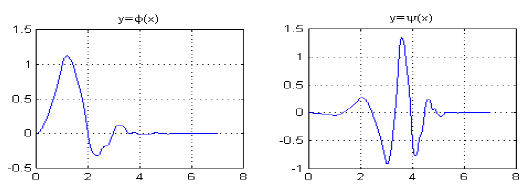
Рис. 3. Масштабирующая вейвлет-функция и материнский вейвлет Добеши D4
С целью повышения скорости вычисления свертки (13) предлагается её вычислять в системе остаточных классов, тогда выбирая модуль pj свертка может быть выражена как:
 |
(15) |
Система остаточных классов и модулярные вычисления являются практически иде- альным инструментом реализации линейной свертки, поскольку операции сложения, вы- читания и умножения выполняются очень просто, а именно, если даны два числа A и B, представленные в системе остаточных классов (с набором взаимно простых оснований m1, m2,...,mL) следующим образом:
A=(a1,a2,...,aL):A≡a1(mod m1), A≡a2(mod m2),...,A≡aL(mod mL),
B=(b1,b2,...,bL):B≡b1(mod m1), B≡b2(mod m2),...,B≡bL(mod mL), (17)
 |
(18) |
Математические модели (17-19) вычисляются на основе использования нейронных сетей конечного кольца [3], число которых определяется рядом каналов по числу оснований, работающих независимо друг от друга и параллельно во времени. Если каждую нейронную сеть конечного кольца отожествить с отдельным основанием системы остаточных классов, то образованная совокупность каналов будет представлять собой арифметическое устройство выполняющее с большой эффективностью вейвлет – преобразование сигналов.
Итак, система остаточных классов является наиболее подходящей технологи- ей для реализации высокоэффективного вейвлет – преобразования для задач цифро- вой обработки сигналов.
Для эффективной реализации операций вейвлет – преобразования по алго- ритму Малла на основе свертки предлагается использовать математическую модель вычислительного объекта, оперирующую числами, представленными в системе оста- точных классов.
Литература
- Добеши И. Десять лекций по вейвлетам. – М.: Ижевск: РХД, 2001.
- Daubechies I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis //IEEE Trans. Inform. Theory, 1990, № 5. P. 961-1005.
- Червяков Н. И., Сахнюк П. А., Шапошников А. В., Макоха А. Н. Под редакцией А. И. Га- лушкина. Учебное пособие для ВВУЗов. – М.: Радиотехника, 2003. – 272 с.
- Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 604 с.
- Астафьева Н.М. Вейвлет-анализ: основы теории и некоторые приложения // Успехи физических наук, 1996, № 11. С. 1145-1170.
- Goswami J.C., Chan A.K. Fundamentals of Wavelets. Theory, Algorithms, and Applications. Wiley, 2000. – 306 p.
- Прокис Дж. Цифровая связь. – М.: Радио и связь, 2000. – 800 с.
- Желудев В.А. О вейвлетах на базе периодических сплайнов // Докл. РАН, 1994, № 1. С. 9-13.
- Новиков Л.В. Основы вейвлет-анализа сигналов. Учебное пособие. – СПб., 1999. – 152 с.