Назад в библиотеку
Кластерная реализация параллельных итерационных методов решения жестких задач Коши
Автор: Никишин Р.Ю., Назарова И.А., Фельдман Л.П.
Источник: Информационные управляющие системы и компьютерный мониторинг (ИУС-2013) / Материалы IV международной научно-техническая конференции студентов, аспирантов и молодых ученых. — Донецк, ДонНТУ — 2013, Т. 2. – С. 235-241.
Аннотация
Никишин Р.Ю., Назарова И. А.,Фельдман Л.П. Кластерная реализация параллельных итерационных методов решения жестких задач Коши
Рассматриваются параллельные алгоритмы решения нелинейной задачи Коши. Выполняется анализ решения одного дифференциального уравнения и системы таких уравнений большой размерности. Приведены особенности выполнения параллельной реализации алгоритмов. Проанализированы аналитические оценки динамических характеристик и зависимости от топологии. Произведено сравнение аналитических и полученных экспериментально характеристик, а также определена эффективность параллельной реализации.
Постановка проблемы.
Применение параллельных
вычислительных систем является стратегическим направлением развития современной
компьютерной индустрии. Это обстоятельство вызвано не столько принципиальным
ограничением максимально возможного быстродействия последовательных машин, сколько
наличием вычислительных задач, для решения которых возможностей существующих
средств вычислительной техники является недостаточным. К таким задачам
относится решение систем обыкновенных дифференциальных уравнений большой
размерности, используемое при моделировании различных динамических процессов с
сосредоточенными параметрами.
В докладе рассматривается
реализация полностью неявных методов типа Рунге-Кутты на кластере.
Анализ реализации ПНМРК
Для системы из  обыкновенных дифференциальных
уравнений:
обыкновенных дифференциальных
уравнений:
 (1)
(1)
где 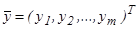 ,
,  - правая часть есть в общем случае
нелинейная функция
- правая часть есть в общем случае
нелинейная функция  , задающая отображение:
, задающая отображение:  .
.
Одношаговый многостадийный метод
для решения нелинейной задачи Коши, описываемой СОДУ (1), имеет вид:
 , (2)
, (2)
где s-размерные вектора  ,
,  и
и  матрица
матрица  ,
, описывают уникальный вариант метода и
выбираются из соображений точности.
описывают уникальный вариант метода и
выбираются из соображений точности.
Применение полностью неявных
многостадийных методов (ПНММ) требует для определения коэффициентов  решения системы
решения системы 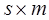 , в общем случае
нелинейных, уравнений:
, в общем случае
нелинейных, уравнений:
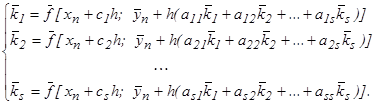 (3)
(3)
Решение системы (3) может быть
получено с использованием следующей итерационной схемы:
 (4)
(4)
где 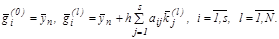
Здесь итерационный процесс,
повторенный  раз
представляет
раз
представляет 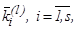 как
как  тую аппроксимацию для
шагового коэффициента
тую аппроксимацию для
шагового коэффициента  .
.
Решение уравнения
Для определения коэффициентов  необходимо решить систему
из s, в общем случае нелинейных,
уравнений:
необходимо решить систему
из s, в общем случае нелинейных,
уравнений:
 (5)
(5)
Для решения системы выбран метод
простой итерации с итерационной схемой, описанной (3).
Вычисление l-й итерации отображено на схеме:
 (6)
(6)
Количество итераций  равняется порядку метода r.
равняется порядку метода r.
Выполнение нулевой итерации, как
и последующих, разбивается на количество процессоров. При этом на каждом из
процессоров выполняется расчет s/p коэффициентов k. Где s – порядок метода, а p
– количество процессоров.
В параллельном алгоритме, после
каждой итерации (как нулевой, так и каждой из  последующих) выполняется множественная
пересылка типа «все-всем» между процессорами. Каждый процессор передает
коэффициенты, хранящиеся в переменной kproc всем процессорам, кроме себя. После
решения системы (4), на каждом процессоре выполняется вычисление
последующих) выполняется множественная
пересылка типа «все-всем» между процессорами. Каждый процессор передает
коэффициенты, хранящиеся в переменной kproc всем процессорам, кроме себя. После
решения системы (4), на каждом процессоре выполняется вычисление  по формуле:
по формуле:  .
.
Аналитические динамические
характеристики метода:
 (7)
(7)
Данные формулы были подтверждены
проведенным экспериментом на MPI-кластере. При проведении
эксперимента используется топология однонаправленное кольцо.
Экспериментальные значения
динамических характеристик последовательного и параллельного алгоритмов приведены в табл.1:
|
Порядок метода
|
Послед.
алгоритм
|
2 процессора
|
|
Время
|
Ускорение
|
|
2
|
0,0000164
|
0,0000302
|
0,543046
|
|
4
|
0,0000329
|
0,0000516
|
0,637597
|
|
6
|
0,000052
|
0,0000698
|
0,744986
|
|
8
|
0,00037
|
0,0000812
|
4,55665
|
|
10
|
0,000193
|
0,000203
|
0,950739
|
Табл. 1 Экспериментальные значения
динамических характеристик последовательного и параллельного алгоритмов
Решение системы уравнений
Для определения коэффициентов  необходимо решить систему
из
необходимо решить систему
из 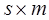 , в общем случае
нелинейных, уравнений:
, в общем случае
нелинейных, уравнений:
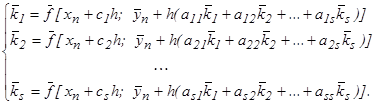 (8)
(8)
Для решения системы выбран метод
простой итерации с итерационной схемой, описанной (3).
На нулевой итерации выполняется
вычисление функций уравнений с аргументами  :
:
 (9)
(9)
На последующих  итерациях выполняется вычисление
коэффициентов
итерациях выполняется вычисление
коэффициентов 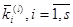 ,
используя коэффициенты
,
используя коэффициенты 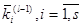 из
предыдущей
из
предыдущей  -й
итерации.
-й
итерации.
Количество процессоров равномерно
делится на порядок метода, таким образом составляя s групп. Каждая группа
вычисляет m уравнений в каждом векторе  . В случае, если процессоров больше, чем
порядок метода, уравнения в каждой группе соответственно делятся между
процессорами группы. Таким образом, каждый процессор в группе вычисляет d
элементов
. В случае, если процессоров больше, чем
порядок метода, уравнения в каждой группе соответственно делятся между
процессорами группы. Таким образом, каждый процессор в группе вычисляет d
элементов  , где
, где  , а
, а  Вычисление
Вычисление  разбивается на p процессоров. На
каждом процессоре вычисляется m/p элементов вектора
разбивается на p процессоров. На
каждом процессоре вычисляется m/p элементов вектора  .
.
Аналитические динамические
характеристики метода:
 (10)
(10)

Данные формулы были подтверждены
проведенным экспериментом на MPI-кластере. При проведении
эксперимента используется топология однонаправленное кольцо.
Экспериментальные значения
динамических характеристик последовательного и параллельного алгоритмов для
методов второго порядка представлены в табл. 2:
|
Кол-во уравнений
|
Послед.
алгоритм
|
2 процессора
|
4 процессора
|
|
Время
|
Ускорение
|
Время
|
Ускорение
|
|
4
|
0,0000115
|
0,0000736
|
0,15625
|
0,000333
|
0,034535
|
|
40
|
0,000624
|
0,00211
|
0,295735
|
0,000706
|
0,883853
|
|
400
|
0,10277
|
0,10517
|
0,97718
|
0,04925
|
2,086701
|
|
4000
|
7,90148
|
3,37831
|
2,338885
|
4,52561
|
1,745948
|
|
8000
|
32,92852
|
14,69011
|
2,241543
|
19,62485
|
1,677899
|
Табл. 2 Экспериментальные значения динамических характеристик последовательного и параллельного алгоритмов для методов второго порядка
Экспериментальные значения
динамических характеристик последовательного и параллельного алгоритмов для
методов четвертого порядка представлены в табл. 3:
|
Кол-во уравнений
|
Послед.
алгоритм
|
4 процессора
|
8 процессоров
|
|
Время
|
Ускорение
|
Время
|
Ускорение
|
|
4
|
0,0000334
|
0,000685
|
0,048759
|
0,0054
|
0,006185
|
|
40
|
0,00353
|
0,01237
|
0,285368
|
0,00436
|
0,809633
|
|
400
|
0,34222
|
0,588
|
0,582007
|
0,207955
|
1,645644
|
|
4000
|
25,8134
|
17,354
|
1,487461
|
15,496
|
1,665811
|
|
8000
|
108,9928
|
58,7362
|
1,855632
|
70,1942
|
1,552732
|
Табл. 3 Экспериментальные значения динамических характеристик последовательного и параллельного алгоритмов для методов четвертого порядка
Анализирую полученные в
результате эксперимента значения, можно сделать вывод о целесообразности
применения параллельных алгоритмов при решении жестких задач Коши ПНМРК.
Выводы
Рассмотрены параллельные
алгоритмы решения нелинейной задачи Коши. Выполнен анализ решения одного
дифференциального уравнения и системы таких уравнений большой размерности.
Оговорены особенности
выполнения параллельной реализации алгоритмов. Проанализированы аналитические
оценки динамических характеристик.
Проведены эксперименты на MPI-кластере, подтверждающие
аналитические оценки и позволяющие наглядно проиллюстрировать эффективность
использование параллельных алгоритмов при решении жестких задач Коши.
Список источников
- Хайрер Э., Нёрсетт С., Ваннер
Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с
англ. – М.: Мир, 1990. – 512с.
- Хайрер Э., Ваннер Г. Решение
обыкновенных дифференциальных уравнений. Жесткие и
дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.
- Фельдман Л.П., Назарова И.А. Эффективность параллельных алгоритмов оценки
локальной апостериорной погрешности для численного решения задачи Коши //
Электронное моделирование, т. 29, № 3, 2007. – С. 11-25.
 , (2)
, (2)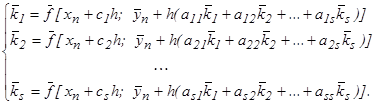 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (9)
(9) (10)
(10)
