Назад в библиотеку
Параллельные неявыные методы решения жестких задач Коши для систем обыкновенных дифференциальных уравнений
Автор: Никишин Р.Ю., Назарова И.А.,Фельдман Л.П.
Источник: Информатика и компьютерные технологии (ИУС-2012) / Материалы VIII международной научно-техническая конференции студентов, аспирантов и молодых ученых. — Донецк, 2012. – Т. 2. – С. 91-95.
Аннотация
Никишин Р.Ю., Назарова И.А., Фельдман Л.П. Параллельные неявыные методы решения жестких задач Коши для систем обыкновенных дифференциальных уравнений. Рассматриваются параллельные алгоритмы решения нелинейной задачи Коши и их отображение на параллельной архитектуре разной топологии, приведены результаты применения теории изоэффективного анализа для оценки масштабируемости параллельных вычислений.
Введение
Применение параллельных вычислительных систем является стратегическим направлением развития современной компьютерной индустрии.
Это обстоятельство вызвано не столько принципиальным ограничением максимально возможного быстродействия последовательных машин, сколько наличием вычислительных задач, для решения которых возможностей существующих средств вычислительной техники является недостаточным.
К таким задачам относится решение систем обыкновенных дифференциальных уравнений большой размерности, используемое при моделировании различных динамических процессов с сосредоточенными параметрами.
В докладе приводятся параллельные алгоритмы одношаговых методов численного решения задачи Коши, которые могут применяться для решения, как жестких, так и нежестких задач, а также исследуется эффективность их отображения на параллельные структуры различной архитектуры и топологии.
Для системы из m обыкновенных дифференциальных уравнений:
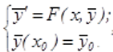
где 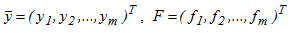 - правая часть есть в общем случае нелинейная функция
- правая часть есть в общем случае нелинейная функция 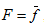 , задающая отображение:
, задающая отображение: 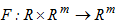 .
.
Одношаговый многостадийный метод для решения нелинейной задачи Коши, описываемой СОДУ, имеет вид:
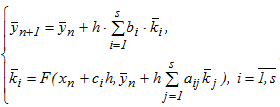
где s-размерные вектора 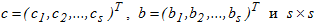 - матрица
- матрица 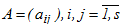 описывают уникальный вариант метода и выбираются из соображений точности. Вид матрицы A задает тип численной схемы, положенной в основу метода. Если ai,j=0 при i≤j, то метод является явным и при наличии малой степени параллелизма, обладает условной устойчивостью. При полностью заполненной матрице имеем полностью неявную схему, применяемую для решения жестких задач.
описывают уникальный вариант метода и выбираются из соображений точности. Вид матрицы A задает тип численной схемы, положенной в основу метода. Если ai,j=0 при i≤j, то метод является явным и при наличии малой степени параллелизма, обладает условной устойчивостью. При полностью заполненной матрице имеем полностью неявную схему, применяемую для решения жестких задач.
Класс неявных численных схем представлен в докладе двумя типами методов: блочные одношаговые методы и полностью неявные методы типа Рунге-Кутты (ПНМРК). К достоинствам полностью неявных, одношаговых методов общего вида (на основе квадратурных формул Радо и Лобатто [1]) следует отнести хорошие характеристики устойчивости и точности, достаточные для решения жестких задач. Недостатками этих методов является высокая вычислительная сложность, обусловленная итерационным процессом определения стадийных коэффициентов, которая не позволяет эффективно применять эти методы на последовательных машинах.
Очевидно, что в отличие от явных методов применение полностью неявных многостадийных методов (ПНММ) требует для определения коэффициентов 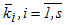 решения системы s x m , в общем случае нелинейных, уравнений:
решения системы s x m , в общем случае нелинейных, уравнений:
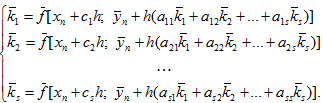
Решение данной системы может быть получено с использованием следующей итерационной схемы:
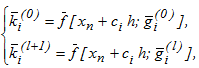
где 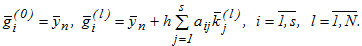
Здесь итерационный процесс, повторенный l-раз представляет 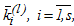 как l-тую аппроксимацию для шагового коэффициента
как l-тую аппроксимацию для шагового коэффициента 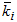 .
.
Скорость сходимости итерационного процесса может быть определена следующим образом: 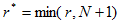 , где r-порядок используемого ПНММ.
, где r-порядок используемого ПНММ.
Блочные или многоточечные неявные методы решения задачи Коши особенно актуальны, поскольку хорошо согласуются с архитектурой параллельных ВС и не требуют вычисления значений в промежуточных точках, что значительно повышает эффективность счета. Данные методы обладают высокой устойчивостью и, что наиболее существенно, являются изначально параллельными, так как позволяют получать решение одновременно в нескольких точках сетки интегрирования.
Множество точек равномерной сетки 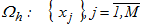 разбивается на N блоков, каждый из которых содержит k точек. Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из k точек может быть записано в виде:
разбивается на N блоков, каждый из которых содержит k точек. Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из k точек может быть записано в виде:
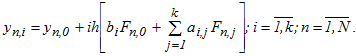
Разложением в ряд Тейлора входящих в невязку функций можно показать, что одношаговый k-точечный блочный метод имеет наивысший порядок аппроксимации равный k+1, следовательно, локальная ошибка в узлах блока имеет порядок 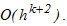 . Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений.
. Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений.
Одним из способов получения решения является метод простой функциональной итерации:
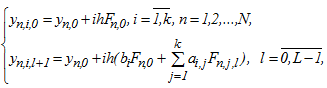
где 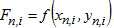 , n - номер блока, n = 1,2,…,N;
, n - номер блока, n = 1,2,…,N;
i - номер точки блока, 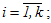 ;
;
l - номер текущей итерации 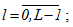 ;
;
L - максимальное число ненулевых итераций.
В отличие от явных методов решения СОДУ, реализация альтернативных способов оценки апостериорной локальной погрешности на основе блочных методов связана с рядом особенностей:
- нет соответствующих последовательных аналогов, следовательно, требуется разработать и обосновать метод оценки локальной погрешности;
- варьировать шаг интегрирования возможно только после вычисления всех значений в k узлах текущего n-го блока,
- при условии неудовлетворительной оценки локальной погрешности и необходимости изменения шага интегрирования практически все вычисления для точек блока окажутся напрасными (некоторые обращения к правой части могут быть использованы вновь).
Для минимизации вычислительные затраты и достижения некоторой заданной точности приближенного решения, численный алгоритм должен иметь механизм управления шагом интегрирования. Это возможно на основе информации об апостериорной локальной погрешности. Для реализации поставленной цели использовались альтернативные способы оценки погрешности на шаге:
- дублирование шага по правилу Рунге;
- вложенные пары схем;
- технология локальной экстраполяции Ричардсона.
Разработка параллельных алгоритмов осуществлялась по иерархической декомпозиционной методике с использованием аппарата графов влияния. Определение теоретических характеристик параллелизма выполнялось с помощью пакета Mathematica (Wolfram Research Inc.), программная реализация выполнена при использовании стандарта передачи сообщений MPI на языке С++.
Проведем сравнение двух классов неявных методов при последовательной и параллельной реализациях на основе наиболее эффективного способа оценки локальной погрешности, а, именно, вложенных формул. Основными параметрами, характеризующими ПНМРК, являются: порядок метода r и число стадий s, причем эти величины являются взаимосвязанными. Кроме того, при решении систем нелинейных алгебраических уравнений для определения стадийных коэффициентов появляется такой параметр, как необходимое число итераций: L. Соответственно, вычислительная сложность блочных методов зависит от порядка метода r, числа точек в блоке k и также числа итераций для получения решения СНАУ необходимой точности: 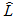 . Для того, чтобы сравнение численных методов на базе неявных одношаговых схем было корректным, необходимо:
. Для того, чтобы сравнение численных методов на базе неявных одношаговых схем было корректным, необходимо:
- обеспечить один и тот же порядок точности, r;
- получить решение в одинаковом числе новых точек, k;
- порождаемые итерационные процессы должны реализовывать предельное число итераций, предусмотренное каждым из рассматриваемых методов: L=2s и
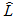 =k.
=k.
Для широко применяемых ПНМРК по теоремам Батчера число стадий связано с порядком метода одним из следующих соотношений [2]: метод Гаусса r=2s; методы Радо r=2s-1; методы Лобатто r=2s-2. Возьмем соотношение r=2s, тем самым намеренно выбирая лучший вариант для ПНМРК. В то же время для блочных одношаговых методов порядок может быть определен через число точек одного блока: r=k+1. Тогда, число стадий ПНМРК и число точек в блоке многоточечного метода связаны следующим соотношением: r=2s=k+1 ⇒ k=2s-1. Используя полученные соотношения, приведем все временные характеристики к одному параметру, пусть это будет число стадий s. Заметим, что среди множества неявных методов типа Рунге-Кутты для сравнения выбраны именно полностью неявные методы, поскольку они обладают идентичными характеристиками устойчивости, что и блочные одношаговые методы, а также в силу оптимального соотношения между порядком и числом стадий методов.
Сравним времена выполнения последовательных алгоритмов рассматриваемых методов. При доминировании в вычислениях времени обращения к правой части ОДУ объем вычислений для ПНМРК в s раз больше, чем для блочных методов, аналогично, для параллельного выполнения алгоритмов имеем - в 2s раз.
Для тривиальной правой части получается аналогичный результат, последовательная и параллельная реализации вычисления решения в новых k точках сетки интегрирования требуют больших накладных расходов для неявных методов Рунге-Кутты по сравнению с блочными методами. Заметим, что для параллельных алгоритмов эта разница увеличивается почти в 2 раза, что подтверждается проведенным экспериментом на тестовых задачах.
Оценка эффективности распараллеливания производится на основе показателей ускорения вычислений (рис. 1-2) по сравнению со своим последовательным алгоритмом (абсолютный коэффициент ускорения) и по сравнению с наилучшим из рассмотренных последовательных алгоритмов (относительный коэффициент ускорения) [3].
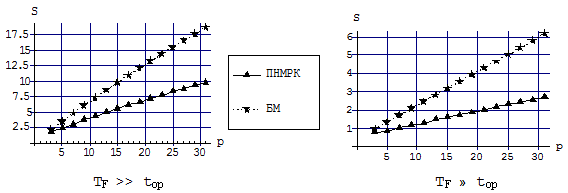 Рис. 1. Графики зависимости абсолютных коэффициентов ускорения вложенных ПНМРК и блочных одношаговых методов от числа процессоров
Рис. 1. Графики зависимости абсолютных коэффициентов ускорения вложенных ПНМРК и блочных одношаговых методов от числа процессоров
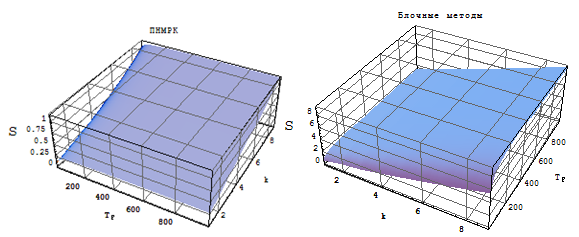 Рис. 2. Графики зависимости относительных коэффициентов ускорения вложенных ПНМРК и блочных одношаговых методов от сложности правых частей и числа точек в блоке
Рис. 2. Графики зависимости относительных коэффициентов ускорения вложенных ПНМРК и блочных одношаговых методов от сложности правых частей и числа точек в блоке
На основе аналогичных исследований можно сделать вывод, что для любых способов оценки локальной погрешности блочные многоточечные одношаговые методы являются наиболее эффективными с точки зрения вычислительных затрат по сравнению с полностью неявными методами Рунге-Кутты.
Выводы
Теоретические исследования и программная реализация параллельных численных методов решения задачи Коши осуществлялась в рамках государственной программы фундаментальных исследований кафедры прикладной математики и информатики по разработке библиотеки параллельного численного анализа для кластера WCCS-2003 Донецкого национального технического университета. Windows Computer Cluster Server-2003 представляет собой кластер, состоящий из головного и вычислительных узлов, следующей конфигурации: Intel Core 2 Duo 1,86 Ghz, 1Гб ОЗУ, HDD объемом 120 Гб, Realtek RTL8168/8111 PCI-E Gigabit Ethernet NIC.
Характерной особенностью WCCS является использование корпоративной структуры Active Directory для обеспечения безопасности, управления учетными записями пользователей. WCCS поддерживает различные сетевые топологии, представляющих собой объединение некоторых из сетей: сеть общего доступа, частная сеть, MPI-сеть. Тестирование параллельных приложений производилось на базе реализации MPICH-2.2 для OS Windows.
Список источников
- Хайрер Э., Нёрсетт С., Ваннер
Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с
англ. – М.: Мир, 1990. – 512с.
- Хайрер Э., Ваннер Г. Решение
обыкновенных дифференциальных уравнений. Жесткие и
дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.
- Фельдман Л.П., Назарова И.А. Эффективность параллельных алгоритмов оценки
локальной апостериорной погрешности для численного решения задачи Коши //
Электронное моделирование, т. 29, № 3, 2007. – С. 11-25.
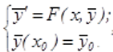
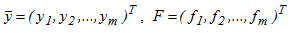 - правая часть есть в общем случае нелинейная функция
- правая часть есть в общем случае нелинейная функция 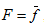 , задающая отображение:
, задающая отображение: 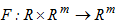 .
.
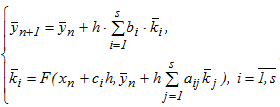
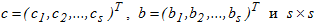 - матрица
- матрица 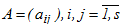 описывают уникальный вариант метода и выбираются из соображений точности. Вид матрицы A задает тип численной схемы, положенной в основу метода. Если ai,j=0 при i≤j, то метод является явным и при наличии малой степени параллелизма, обладает условной устойчивостью. При полностью заполненной матрице имеем полностью неявную схему, применяемую для решения жестких задач.
описывают уникальный вариант метода и выбираются из соображений точности. Вид матрицы A задает тип численной схемы, положенной в основу метода. Если ai,j=0 при i≤j, то метод является явным и при наличии малой степени параллелизма, обладает условной устойчивостью. При полностью заполненной матрице имеем полностью неявную схему, применяемую для решения жестких задач. 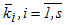 решения системы s x m , в общем случае нелинейных, уравнений:
решения системы s x m , в общем случае нелинейных, уравнений: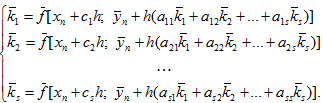
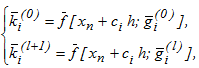
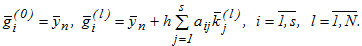
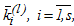 как l-тую аппроксимацию для шагового коэффициента
как l-тую аппроксимацию для шагового коэффициента 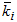 .
.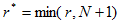 , где r-порядок используемого ПНММ.
, где r-порядок используемого ПНММ.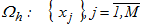 разбивается на N блоков, каждый из которых содержит k точек. Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из k точек может быть записано в виде:
разбивается на N блоков, каждый из которых содержит k точек. Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из k точек может быть записано в виде: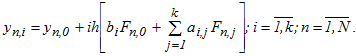
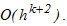 . Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений.
. Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений. 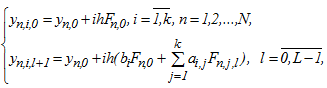
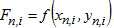 , n - номер блока, n = 1,2,…,N;
, n - номер блока, n = 1,2,…,N;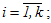 ;
;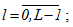 ;
;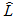 . Для того, чтобы сравнение численных методов на базе неявных одношаговых схем было корректным, необходимо:
. Для того, чтобы сравнение численных методов на базе неявных одношаговых схем было корректным, необходимо:
