Назад в библиотеку
Параллельные вложенные блочные неявные методы решения
жестких задач Коши
Автор:
Фельдман Л.П., Назарова И.А., Михайлова Т.В.
Источник:
Искусственный интеллект. Интеллектуальные системы (ИИ-2011) / Материалы
международной научно-технической конференции. - Донецк: ІПШІ «Наука і освіта», т.1, 2011. – С.
57–61.
Аннотация
Фельдман Л.П., Назарова И.А., Михайлова Т.В. Параллельные вложенные блочные
неявные методы решения жестких задач Коши.
Рассматриваются параллельные алгоритмы
решения нелинейной задачи Коши и их отображение на параллельной архитектуре разной
топологии, приведены результаты применения теории изоэффективного анализа для оценки
масштабируемости параллельных вычислений.
Введение
Исследование методов решения задачи Коши показало, что параллельные свойства таких
методов во многом определяются видом лежащей в их основе численной схемы. Наименее
трудоемкими являются явные методы, однако присущие этим схемам недостатки, в частности
условная устойчивость, существенно ограничивают область их применения. В этой связи
значительный интерес представляют неявные схемы, которые не имеют альтернативы при
решении жестких задач [1-2].
Данная статья посвящена разработке, обоснованию параллельных алгоритмов решения
задачи Коши с встроенными способами оценки локальной погрешности на основе неявных
одношаговых блочных многоточечных методов, а также построению и исследованию
эффективности их отображений на реальные параллельные системы SIMD, MIMD-архитектуры
и кластерные системы с распределенной памятью.
Блочные методы решения задачи Коши
Рассматривается численное решение задачи Коши, ассоциируемое с решением СОДУ
первого порядка с известными начальными условиями:
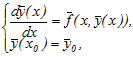 (1)
(1)где правая часть системы есть в общем случае нелинейная функция,
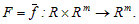 Блочные методы решения задачи Коши особенно актуальны, поскольку хорошо согласуются с
архитектурой параллельных систем и не требуют вычисления значений в промежуточных
точках, что значительно повышает эффективность счета. Данные методы обладают высокой
устойчивостью и являются изначально параллельными [2], так как позволяют получать решение
одновременно в нескольких точках сетки интегрирования.
Блочные методы решения задачи Коши особенно актуальны, поскольку хорошо согласуются с
архитектурой параллельных систем и не требуют вычисления значений в промежуточных
точках, что значительно повышает эффективность счета. Данные методы обладают высокой
устойчивостью и являются изначально параллельными [2], так как позволяют получать решение
одновременно в нескольких точках сетки интегрирования.
Пусть множество точек равномерной сетки
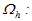
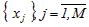 разбивается на
N блоков.
Каждый блок содержит
k точек и при этом
N≤M. В пределах блока все точки равноудалены друг
от друга:
разбивается на
N блоков.
Каждый блок содержит
k точек и при этом
N≤M. В пределах блока все точки равноудалены друг
от друга: 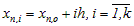 , где
, где 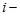 номер точки в блоке,
номер точки в блоке,
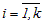 ;
; 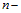 номер блока,
номер блока,
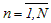 ;
; 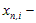 точка с номером
i, принадлежащая блоку
n;
точка с номером
i, принадлежащая блоку
n; 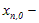 начальная точка
n-го блока;
начальная точка
n-го блока;
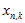 – конечная
точка n-го блока. Множество точек
– конечная
точка n-го блока. Множество точек
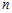 -го блока из
-го блока из 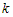 точек обозначается
точек обозначается
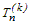 . При этом имеет
место равенство:
. При этом имеет
место равенство: 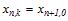 . Пусть
. Пусть 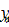 приближенное значение решения задачи Коши в точке
приближенное значение решения задачи Коши в точке
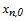 .
.
Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из
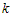 точек имеет вид:
точек имеет вид:
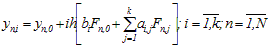 . (2)
. (2)Блочные параллельные методы относятся к классу неявных, поэтому для вычисления
приближенных значений решения задачи Коши необходимо разрешить систему нелинейных
уравнений. Одним из способов получения решения является метод простой функциональной
итерации:
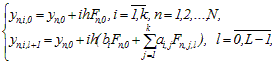 (3)
(3)где 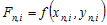 , n – номер блока,
n = 1,2,…,N;i – номер точки блока,
, n – номер блока,
n = 1,2,…,N;i – номер точки блока,
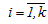 ;
; 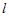 – номер
текущей итерации
– номер
текущей итерации 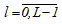 ;
; 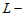 максимальное число ненулевых итераций.
максимальное число ненулевых итераций.
Вложенные блочные методы решения задачи Коши
Идея вложенных форм, предложенная для оценки локальной погрешности численного
решения обыкновенных дифференциальных уравнений методами типа Рунге-Кутты, может быть
использована и для одношаговых блочных многоточечных методов на основе двух различных
подходов:
1) комбинация независимых формул разных порядков точности;
2) комбинация специально подобранных формул разных порядков точности.
Первый подход заключается в применении двух различных независимых блочных
методов смежных порядков точности
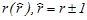 на одной и той же сетке интегрирования:
на одной и той же сетке интегрирования:
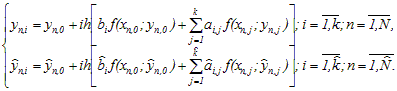 (4)
(4)Такой подход к оценке локальной погрешности является более эффективным по сравнению с
правилом Рунге, поскольку при достаточной простоте позволяет уменьшить вычислительные
затраты. Так, для применения правила дублирования шага необходимо решить три СНАУ
размерности 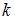 , а для применения вложенного метода две системы: одну той же размерности,
другую размерности
, а для применения вложенного метода две системы: одну той же размерности,
другую размерности
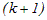 .
.
Второй подход к разработке блочных вложенных методов предполагает использование идеи
последовательного повышения порядка точности [3]. Таким образом, для оценки локальной
погрешности могут быть выбраны две произвольные, подряд идущие, аппроксимации решения.
При использовании 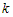 -точечного метода, все дополнительные вычислительные расходы на
определение локальной погрешности сводятся к дополнительному итерированию (в рамках
предельных значений) при решении системы нелинейных уравнений размерности
-точечного метода, все дополнительные вычислительные расходы на
определение локальной погрешности сводятся к дополнительному итерированию (в рамках
предельных значений) при решении системы нелинейных уравнений размерности
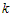 . Расчетные
формулы для одного,
. Расчетные
формулы для одного, 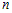 -го, блока вложенного многоточечного метода №2 имеют вид:
-го, блока вложенного многоточечного метода №2 имеют вид:
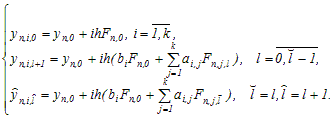 (5).
(5).Проведенные исследования качества параллельных одношаговых схем решения задачи Коши
позволяют сделать вывод, что из двух предложенных методов вложенных форм для блочных
способов решения нелинейной задачи Коши, второй метод обладает несомненными
преимуществами.
Выводы
Теоретические исследования и программная реализация параллельных численных методов
решения задачи Коши осуществлялась в рамках государственной программы фундаментальных
исследований кафедры прикладной математики и информатики по разработке библиотеки
параллельного численного анализа для кластера
WCCS-2003 Донецкого национального
технического университета.
Windows Computer Cluster Server-2003 представляет собой кластер,
состоящий из головного и вычислительных узлов, следующей конфигурации:
Intel Core 2 Duo
1,86 Ghz, 1Гб ОЗУ, HDD объемом 120 Гб,
Realtek RTL8168/8111 PCI-E Gigabit Ethernet NIC.
Характерной особенностью
WCCS является использование корпоративной структуры
Active
Directory для обеспечения безопасности, управления учетными записями пользователей.
WCCS
поддерживает различные сетевые топологии, представляющих собой объединение некоторых из
сетей: сеть общего доступа, частная сеть,
MPI-сеть. Тестирование параллельных приложений
производилось на базе реализации
MPICH-2.2 для
OS Windows.
Литература
1. Хайрер Э., Ваннер. Г. Решение ОДУ. Жесткие задачи. - М.: Мир, 1999.- 685с.
2. Фельдман Л.П., Назарова И.А
. Параллельные алгоритмы численного решения задачи Коши
для систем обыкновенных дифференциальных уравнений // Математическое моделирование,
т.18, № 9, 2006, с. 17-31.
3. Фельдман Л.П., Назарова И.А. Эффективность параллельных алгоритмов оценки локальной
апостериорной погрешности для численного решения задачи Коши // Электронное
моделирование, т. 29, № 3, 2007. - С.11-25.
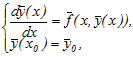 (1)
(1)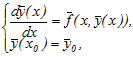 (1)
(1)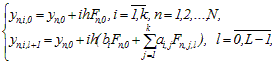 (3)
(3)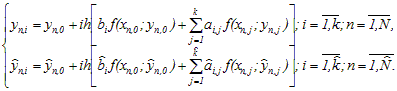 (4)
(4)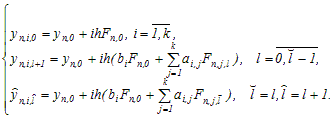 (5).
(5).