МУЛЬТИФРАКТАЛЬНЫЙ И ТОПОЛОГИЧЕСКИЙ АНАЛИЗ СЛОЖНОСТИ МАГНИТНОГО ПОЛЯ СОЛНЦА
Автор: А. МИЛЬКОВ, И.С. КНЯЗЕВА, Н.Г. МАКАРЕНКО
Источник: http://ru.convdocs.org/docs/index-64395.html
Анализируется динамика солнечных активных областей (АО) на основе MDI-магнитограмм полного диска. В основе подхода лежат методы фрактальной геометрии и вычислительной топологии. Мы оцениваем топологические инварианты – числа Бетти для временной последовательности магнитограмм и полученных из них гельдеровских карт для вспышечных и спокойных АО. Предварительные результаты указывают на существование возможных топологических предвестников перед Х-вспышками. Нашей основной целью является описание динамической эволюции активных областей (АО) Солнца в рамках геометрических и топологических инвариантов, извлеченных из Michelson-Doppler Imager (MDI)-данных. Исследование ориентировано на поиск предвестников сильных солнечных вспышек в контексте этих инвариантов[1-3] .
Основная идея описания эволюции АО заключаются в следующем. MDI представляет собой цифровое изображение, т.е. цифровую функцию яркости I(x)=RxZxZ->R, заданную на решетке целочисленных координат xєZxZ где уровнями серого
кодируется значение радиальной bz компоненты магнитного поля. Пространственное разрешение данных составляет приблизительно 1500x1500 км. Известно, что магнитные числа Рейнольдса в магнитосферных полях достигают значений ~108, что соответствует состоянию полностью развитой турбулентности. Следовательно, основные характеристики поля должны асимптотически удовлетворять степенным законам. Так, для достаточно малой области напряженность поля допускает аппроксимацию
 . Свойства масштабной инвариантности наследуются в текстуре цифрового изображения. Точнее, определим меру Радона m(A) для компактной области AєZxZ магнитограммы размером как |A|=r [3]
. Свойства масштабной инвариантности наследуются в текстуре цифрового изображения. Точнее, определим меру Радона m(A) для компактной области AєZxZ магнитограммы размером как |A|=r [3]

Тогда m(A)~rh(x), (2) где h(x) называют гельдеровскими показателями регулярности меры [2,3]. Преобразование I(x)->h(x) позволяет описать геометрию магнитограммы в масштабно-инвариантных переменных, и визуализацию полученной матрицы назовем гельдеровской картой.
Гельдеровский показатель h(x)=log m(A)/log|x| можно интерпретировать как коэффициент плавучести
[4] магнитных трубок образующие АО, с точностью до выбора логарифмической шкалы. Поэтому так называемые сингулярные многообразия [5]F(h)={x|h(x)=c} , т.е. линии уровня гельдеровских карт, можно рассматривать как топографию различной плавучести
. Многообразия F(h) характеризуют их фрактальной (бокс) размерностью D(h) . Если степенной закон (2) выполняется статистически в достаточно широком диапазоне масштабов, график (h,D(h)), который называют мультифрактальным спектром, является выпуклой кверху функцией, т.е. D(h)<0. Существуют многочисленные попытки (см. например, [6, 7]) использовать изменение формы этого спектра во времени, в рамках известной гипотезы о всплывающем магнитном потоке в АО, как предвестник солнечных вспышек. Однако наши эксперименты со спектрами, полученными с помощью емкостей Шоке [1, 2], не убеждают в существовании надежной статистической связи между вариациями спектра и вспышками [3].
Не исключено, однако, что поток, предваряющий вспышку, может быть обнаружен в изменении топологических характеристик магнитограммы или ее гельдеровской карты: дополнительное поле потока должно менять существующий баланс в текстурных паттернах АО. В качестве дескрипторов текстуры мы использовали топологические инварианты – числа Бетти – и методы вычислительной топологии [8] для получения их оценок. В качестве примера рассмотрим рис. 1. Контур (или цикл) на рис. 1, а является границей заштрихованной области: он может быть стянут в точку непрерывной деформацией. Цикл на рис. 1, б, напротив, границей не является: он может быть стянут только к дыре
– белому пикселю в центре. Число независимых циклов, не являющихся границами, определяет так называемое 1-мерное число Бетти b1. Число компонент связности, образованное пикселями выбранного цвета, определяет 0-мерное число Бетти b0. В нашем примере b1=1, b0=1, если белый цвет считать фоном. Для негативного
изображения (фон – серые пиксели) мы получим b0=1,b1=0.

Рис. 1. Пример построения топологических инвариантов: а – контур (или цикл) является границей заштрихованной области; б – цикл границей не является
Формально, в рамках теории гомологий, рассматривают абелеву группу p-цепей Cp, где p=0 – это точки, p=1 – ребра и p=2 – клетки. Ее подруппу Zp от Cp составляют циклы, т.е. цепи с нулевой границей. Подгруппой Zp являются границы Bp от Zp, т.е. циклы, являющиеся границами p+1 -цепей. Числа Бетти bp являются рангами фактор группы Hp=Zp/Bp.
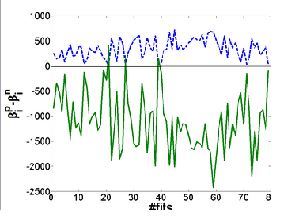
Рис. 2. Разности для вспышечно-спокойной области (АО10923.
На оси ^ Ox указаны номера магнитограмм
Для сечения магнитограммы плоскостью раздела полярностей пиксели черного цвета соответствуют северной полярности, т.е. N-полю, а белые пиксели – S-полю. Можно предположить, что для спокойной
АО разности чисел Бетти, подсчитанные для негатива и позитива MDI–изображений, должны колебаться относительно среднего уровня. Всплытие дополнительного потока, предшествующего вспышке, может приводить к заметному дисбалансу полярности, и, следовательно, проявляться в вариациях чисел Бетти.
Мы использовали магнитограммы (^ MDI-данные) [9] для выборки АО и пакет по обработке цифровых изображений CHomP [10] для получения оценок чисел Бетти и действительно обнаружили ожидаемый эффект всплытия потока для некоторых АО. Разности (позитив-негатив) ведут себя приблизительно симметрично в интервале времени продолжительностью в 60 часов.
Работа выполнена при поддержке гранта РФФИ 07-02-00379а
СПИСОК ЛИТЕРАТУРЫ
- Макаренко Н.Г., Круглун О.А., Каримова Л.М. // Тр. X Пулковской конф. по физике Солнца, Санкт-Петербург. 2006. С. 31.
- Макаренко Н.Г., Круглун О.А., Мухамеджанова С.А. // Тр. XI Пулковской конф. по Физике Солнца. С-Петербург 2007. С. 235
- Круглун О.А., Каримова Л.М, и др. // Солнечно-земная физика. 2007. T. 10. С. 32.
- Acheson D.J. // Solar Physics. 1979. V. 62. P. 23
- Turiel A., Parga N. // Neural Computation 2000. V.12. P. 763
- Salakhutdinova I. I., Golovko A. A. // Solar Physics. 2005. V.225. P. 59
- Conlon P. A., Gallagher P. T. et al. //Solar Physics. 2007. V.241. P.67
- Kaczynski K. Computational Homology / K. Kaczynski, M.M. Mischaikow. Springer-Verlag, 2004.
- MDI Daily Magnetic Field Synoptic Data [Электронный ресурс] ? Режим доступа: http://soi.stanford.edu/magnetic/index5.html
- Computational Homology Project [Электронный ресурс] Режим доступа: http://chomp.rutgers.edu