Задача прогнозирования временных рядов (ВР) может быть сформулирована как задача распознавания образов [1]. При такой формулировке нейронная сеть (НС) используется как универсальное средство аппроксимации дискретной функции, задаваемой наборами обучающей выборки (ОВ). Описание распознаваемой ситуации набора (ОРСН) задает параметры этой функции, а класс набора — ее значение. При задании аппроксимируемой функции, с помощью ОВ, предъявляются два требования — непротиворечивость и полнота задания ее значений.
Известны критерии качества, характеризующие выполнение этих требований для конкретной ОВ — противоречивость и повторяемость выборки [2]. Для их наглядного представления рассмотрим наборы ОВ в качестве точек в многомерном пространстве, задаваемом ОРСН (рис. 1).
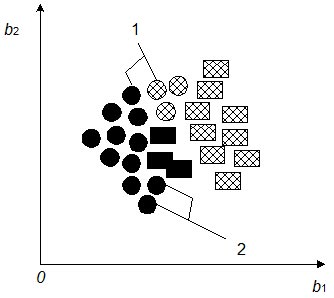
Рис. 1. Представление в многомерном пространстве описания распознаваемой ситуации противоречивых (1) и повторяющихся(2) наборов ОВ
Наборы ОВ, описывающие одинаковые ситуации, изображены в виде объектов одной формы. Закраска объекта определяет класс, к которому принадлежит данный набор. Повторяемость ОВ характеризует нормированное количество одинаковых ситуаций внутри классов — число объектов одной формы и одной закраски. Противоречивость ОВ характеризует нормированное количество одинаковых ситуаций в разных классах — число объектов одинаковой формы и разной закраски. Качество ОВ тем выше, чем меньше ее противоречивость и больше повторяемость [2].
Проблема противоречивого задания аппроксимируемой функции является одной из основных при формировании ОВ. Противоречивость формулировки в задачах распознавания и прогнозирования является признаком неполноты описания распознаваемого объекта. В задаче распознавания образов класс образует естественно сформированную группу объектов, и противоречивость ОВ может быть разрешена путем его изменения для противоречивых объектов. Классы, формируемые при решении задачи прогнозирования, являются искусственными образованиями, каждый из них описывает будущие значения прогнозируемой величины (ПВ) с точностью, не меньшей требуемой точности прогнозирования. Принудительное отнесение объектов, формирующих противоречивость ОВ, к одному из классов является достаточно грубым вмешательством в контекст задачи и приводит к существенному снижению точности прогнозирования [1]. Для задач прогнозирования высокая противоречивость ОВ является признаком того, что способ описания распознаваемой ситуации выбран неудачно. Рассмотрим влияние размера описания (глубины погружения) распознаваемой ситуации на противоречивость ОВ.
Для динамических систем доказана следующая теорема Такенса [3]: если временной ряд порождается динамической системой, т.е. значения ВР есть некоторая функция состояния системы, то ВР может быть рассмотрен как задающий зависимость
bi = ƒ( bk, bk+1,..., bk+(n-1) ) (1)
где { bk, bk+1,..., bk+(n-1) } — описание ситуации, в результате развития которой прогнозируемая величина (ПВ) приняла значение bi и обозначается bin;
n — размер описания ситуации;
k = i - p/t — номер измерения, принадлежащего ряду , с которого начинается описание ситуации;
p — период прогнозирования;
t — шаг временного ряда.
При этом для описания ситуации bin существует такая глубина погружения в прошлое n, которая обеспечивает однозначную зависимость значения ряда bi от его предыдущих значений. В соответствии с теоремой, размер описания ситуации n, обеспечивающий однозначность зависимости (1), приблизительно равен эффективному числу степеней свободы данной динамической системы [3].
Таким образом, изменение размера ОРСН может гарантировать получение непротиворечивой ОВ. Поскольку в задаче прогнозирования ВР размер описания образа не является фиксированной величиной, затраты на его изменение невелики по сравнению с задачей классификации. Увеличение размера описания образа не требует сбора дополнительной информации об объекте и проведения анализа взаимного влияния свойств объекта, а при уменьшении размера описания образа отсутствует опасность исключения существенных свойств объекта. В то же время снижение противоречивости ОВ за счет увеличения размера ОРСН имеет существенный недостаток — вместе с противоречивостью существенно снижается и повторяемость полученной ОВ. Малая повторяемость ОВ приводит к переобучению НС [4] и неспособности сети обобщать полученный опыт на будущие значения ПВ. Для различных участков ВР, различна глубина погружения в прошлое, которая достаточна для обеспечения однозначности зависимости (1). В следствии этого происходит снижение повторяемости ОВ при увеличении размера ОРСН. Таким образом, с одной стороны, на разных участках ВР необходимо формировать образы с разным размером ОРСН, а с другой стороны, размер входных векторов возбуждения обучающих наборов ОВ для НС должен быть одинаков. Описанное противоречие создает проблему выбора размера описания ситуации для нестационарных ВР. Рассмотрим данную проблему и возможные пути ее решения.
Для формального описания проблемы выбора размера ОРСН введем понятия сложности: участка ВР, набора ОВ и ОВ. Для определения сложности участка ВР рассмотрим участок Ak = { astart, astart+1,..., afin } ряда A = { a1, a2,..., an }.
Существует функция ƒ, такая что a'i = ƒ(i, p1, p2,..., pn), где pj(j ∈ 1;s) — параметры функции ƒ; s — количество параметров функции ƒ; i — номер члена ряда Ak. Эта функция задает ряд A'k = { a'start, a'start+1,..., a'fin }, который является аппроксимацией ряда Ak. Рассмотрим случайную величину Xk = Ak - A'k. Значение среднего квадратичного отклонения σxk этой случайной величины есть мера рассеяния значений ряда Ak относительно его аппроксимации A'k.
Вид функции ƒ задает единицу измерения сложности. В качестве единицы измерения может использоваться линейная функция, параболическая, гармонический ряд и т.д. Поскольку наиболее простым типом поведения является линейный тип, в качестве единицы сложности поведения предложено использовать функцию a'i = ip1 + p2,
где i — номер члена ряда A участка k;
p1, p2 — коэффициенты аппроксимации.
Сложность участка ВР εk определяется величиной дисперсии DXk , увеличение значения которой на участке означает усложнение поведения ВР на этом участке. Тогда сложность участка ВР
εk = D(Ak - A'k).
Сложность εi обучающего набора li = { bni, ci } ОВ L = { l1, l2,...,lnl }, где nl — число наборов в ОВ, определим как сложность участка ВР, который писывается вектором bni.
Сложность ОВ L определяется через сложность обучающего набора li.

В соответствии с определением сложности ВР размер формируемых на участке k ряда A ОРСН, необходимый для обеспечения однозначности зависимости (1), зависит от сложности ВР на этом участке. Проанализируем зависимость критериев качества ОВ от ее сложности. Сложность, как следует из определения, зависит от размера участка ряда, на котором она вычисляется.
Чем меньше размер ОРСН, тем меньше сложность и тем выше повторяемость и противоречивость полученной ОВ. Например, при минимальном размере ОРСН, равном одному измерению ВР, максимально число одинаковых образов. Поэтому сложность ОВ — минимальна, повторяемость и противоречивость — максимальны.
Чем больше размер ОРСН, тем выше сложность и тем меньше повторяемость и противоречивость полученной ОВ. При размере описания образа, например, в половину длины ВР, максимально число разных образов. Поэтому сложность ОВ — максимальна, повторяемость и противоречивость — минимальны.
На основании вероятностных параметров процесса формирования ОВ можно доказать, что с ростом сложности образа, повторяемость ОВ падает медленнее, чем ее противоречивость.
Для выявления характера зависимости повторяемости и противоречивости ОВ от сложности образов было исследовано более 40 ВР различного вида (рис. 2). Для каждого из рядов, для различных размеров описания ситуации, производились формирование ОВ и ее анализ. Для каждого ВР, обладающего равномерной сложностью описания, эксперименты показали существование оптимальной сложности образов ОВ, при которой повторяемость и противоречивость ОВ находятся в диапазоне своих оптимальных значений и достигается их оптимальное [2] сочетание, гарантирующее качественное обучение НС.
Таким образом, эксперименты показали, что для ВР, отличие в сложности которого на различных участках не превышает 20%, ОРСН может быть выбран однозначно, что обеспечивает снижение противоречивости и естественную повторяемость ОВ. Последняя в свою очередь отображает реальную полноту описания аппроксимируемой функции.
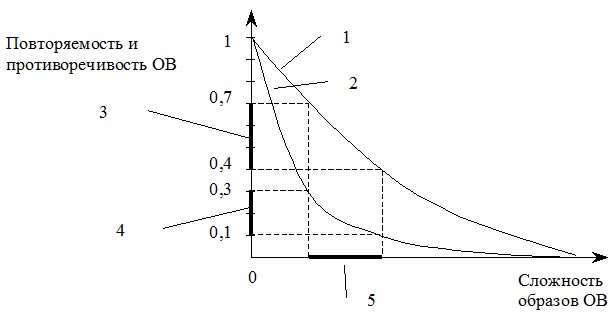
Рис. 2. Зависимость повторяемости(1) и противоречивости (2) ОВ от сложности ее образов; 3,4,5 — оптимальные диапазоны повторяемости, противоречивости и сложности, соответственно
Предложим общий способ получения ВР, обладающих равномерной сложностью, на основании ВР, не обладающих ею. Так как нестационарные ВР обладают различной сложностью на разных участках, предлагается проводить формирование ОВ на основании ВР, содержащего векторы параметров непересекающихся участков исходного ВР. Для получения такого описания, на каждом участке одинаковой сложности, получают его описание с помощью метода сжатия описания функции. К методам сжатия описания функции, которые могут использоваться для получения такого описания, предъявляется ряд требований: обеспечение сжатия описания для обрабатываемого ВР; обеспечение формирования ВР, обладающего равномерной сложностью; минимум вычислительных затрат для перехода к сжатому описанию и обратно.
Эффективным критерием выбора размера описания ситуации в задачах прогнозирования нестационарных ВР методами нейровычислений является сложность образов ОВ. Однако этот критерий не несет информации о путях повышения качества ОВ. В то же время, понятие сложности позволяет выполнить численное обоснование проблемы выбора размера описания ситуации, дополняет предложенные параметры повторяемости и противоречивости, формируя систему показателей, на основании которых возможно построение методики повышения качества ОВ.
Литература
- Weigend A.S., Gershenfield N. A. (Editor) Time series prediction: Forecasting the future and understanding the past. — Boston: Addison—Wesley, 1994.
- Тарасенко Р.А. Крисилов В.А. Предварительная оценка качества обучающей выборки для нейронных сетей в задачах прогнозирования временных рядов. //Тр. Одес. политехн. ун—та. — Одесса, 2001. — Вып. 1. — С.
- Sauer T., Yorke J.A., Casdagli M., Embedology // J. of Statistical Physics. — 1991. — Vol. 65.— P. 579 — 616.
- Fausett L. Fundamentals of Neural Networks. — New York: Prentice Hall, 1994.