К вопросу о границах применимости аналитических и численных решателей уравнений, описывающих движение воздуха в шахтных вентиляционных сетях

Авторы: Гоголенко С.Ю., Святный В.А.
Источник: Наукові праці Донецького національного технічного університету. Серiя "Проблеми моделювання та автоматизації проектування" (МАП-2008). Випуск 7(150): – Донецьк: ДонНТУ. – 2008. – 290 с.

Аннотация

Гоголенко С. Ю., Святный В. А. К вопросу о границах применимости аналитических и численных решателей уравнений, описывающих движение воздуха в шахтных вентиляционных сетях. Движение воздуха в шахтных вентиляционных сетях (ШВС) математически описывается моделями, основанными на нелинейных дифференциальных уравнениях в частных производных (ДУЧП) на геометрических графах. Аналитическое решение таких ДУЧП существует лишь в некоторых специальных случаях. Основным методом численного моделирования динамики воздуха является метод прямых, который позволяет перейти от ДУЧП на графе к гомогенной слабо связной системе обыкновенных дифференциальных уравнений (ОДУ) высокой размерности. В данной статье содержится краткий обзор аналитических решений и теоретический анализ метода прямых в применении к решению ДУЧП, которые описывают динамику воздуха в ШВС. Основное внимание уделено исследованию устойчивости по Ляпунову полудискретизированных ДУЧП и анализу устойчивости численных методов их интегрирования. В статье также приведены с доказательствами некоторые неравенства, которые обеспечивают устойчивость численных методов решения ДУЧП, описывающих движение воздуха в ШВС.

Анотація

Гоголенко С. Ю., Святный В. А. Про межі застосовності аналітичних і чисельних розвязувачів рівнянь, що описують рух повітря в шахтних вентиляційних мережах. Рух повітря в шахтних вентиляційних мережах (ШВМ) математично описується моделями, що ґрунтуються на нелінійних диференціальних рівняннях у частинних похідних (ДРЧП) на геометричних графах. Аналітичне рішення таких ДРЧП існує лише в деяких спеціальних випадках. Основним методом чисельного моделювання динаміки повітря є метод прямих, що дозволяє перейти від ДРЧП на графі до гомогенної слабко зв'язної системи звичайних диференціальних рівнянь (ЗДР) високої розмірності. У даній статті міститься короткий огляд аналітичних рішень і теоретичний аналіз методу прямих у застосуванні до рішення ДРЧП, які описують динаміку повітря у ШВС. Основна увага приділена дослідженню стійкості за Ляпуновим напівдискретизованих ДРЧП і аналізі стійкості чисельних методів їхнього інтегрування. У статті також наведено з доказами ряд нерівностей, що забезпечують стійкість чисельних методів рішення ДРЧП, які описують рух повітря у ШВС.

Abstract

Gogolenko S. Yu., Svjatnyj V. A. To the bounds of usage analytical and numerical solvers of equations that describe air dynamics in mine ventilation networks. Air flow in mine ventilation network is described mathematically by models based on nonlinear PDEs on geometrical graphs. Analytical solutions for such type of PDEs exist only in some special cases. Prevalent method for simulation of these models is half discretization of PDEs using method of lines (MOL) approach. It leads to large homogenous weakly connected ODE systems. This paper contains brief overview of analytical solutions and theoretical analysis of MOL approach for solving of PDEs on graphs that describe air dynamics in mine ventilation networks. The main attention is given on investigation of Lyapunov stability of half discretized PDEs and stability analysis of numerical methods for solving of half discretized PDEs. Some inequalities that provide stability of numerical methods are represented with their proofs in this paper.

Условные обозначения:

Г – граф, описывающий топологию шахтной вентиляционной сети (ШВС);

δГ – граничные (тупиковые) узлы сети;

L(G) – рёберный граф графа G;

G, G_Δξ(Г) – граф вторичной топологи шага для сети Г;

k • i – отношение инцидентности k-го ребра i-му, либо множество рёбер k, инцидентных i-му;

u_k, u(i, j) – k-ое ребро графа исходящее из вершины i и входящее в вершину j;

V – вершинно-рёберная матрица (0, 1, -1)-инциденций;

ℑ, ℑ(G) – лапласиан (матрица полных проводимостей) графа G;

I_n – единичная матрица размерности n х n;

P_A (λ) – характеристический полином матрицы A ;

S_A – множество всех собственных чисел (спектр) матрицы A;

ρ_а – плотность воздуха;

a – скорость звука в воздухе;

p – давление воздуха;

Q – поток воздуха;

S(x) – площадь поперечного сечения выработки.

Введение

Модель движения воздуха в ШВС задаётся нелинейными дифференциальными уравнениями в частных производных (ДУЧП) на геометрических графах. Точные аналитические решения для подобных задач удаётся получить лишь в исключительных случаях. Основным же аппаратом для решения ДУЧП на геометрических графах являются численные методы, среди которых наибольшее распространение получил метод прямых. Данная работа реализует попытку рассмотреть все известные на текущий момент аналитические методы, а также очертить границы применимости численных методов решения ДУЧП, описывающих движение воздуха в ШВС. Как известно, получение адекватного численного решения системы ОДУ возможно лишь при обеспечении сходимости численных методов. Поэтому значительное внимание в статье уделяется вопросам аппроксимации и устойчивости, а также связанному с ними вопросу о максимально точной оценке разброса спектра матриц, характеризующих якобиан системы ОДУ.

Уравнения движения воздуха в ШВС

Уравнения движения воздуха по отдельным выработкам были получены Л. П. Фельдманом [1]. В. А. Святный [2] распространил эти уравнения на случай ШВС. Как показано в [1], основу разработанного Л. П. Фельдманом и В. А. Святным математического описания движения воздуха по ШВС в случае отсутствия выработанных пространств составляет система из двух дифференциальных уравнений в частных производных на геометрическом графе:

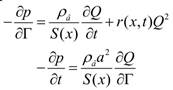(1)

Первое из них объединяет множество уравнений движения, а второе – уравнений неразрывности. Уравнения движения строятся для каждой ветви графа Г, а уравнения неразрывности для каждого узла соответственно. При этом в i-ой ветви ∂p/∂Г выражается через ∂p_i/∂x_ui, где x_ui – пространственная координата вдоль i-ой ветви, а в i-ом узле ∂Q/∂Г – через

Уравнения (1) выводились с учётом следующих допущений [1]:

• режим движения воздуха изотермический;
• сечения и длины выработок постоянны во времени;
• поперечные сечения выработок постоянны вдоль выработок;
• влияние метана на динамику воздушных потоков пренебрежимо мало.

Аналитическое решение для ветви графа ШВС

Продифференцировав первое уравнение системы (1) по времени dt, а второе по пространственной координате dx и далее приравняв левые части полученных соотношений, после незначительных упрощений приходим в случае отдельной выработки к равенству:

(2)

которое соответствует нелинейному гиперболическому уравнению для функции Q(x, t). Если положить, что площадь S не зависит от координаты x, а сопротивление r от времени t, то уравнение (2) значительно упрощается:

(3)

Физически данные предположения обозначают постоянство площади поперечного сечения вдоль выработки и отсутствие регулируемых сопротивлений. Довольно часто подобные условия точно либо приближённо выполняются для отдельных выработок и их участков, а поэтому построение аналитического решения уравнения (3) имеет практическую ценность. При некоторых начальных условиях и значениях параметров a и b для уравнения (3) такие аналитические решения удаётся получить [3]. Автомодальное решение (3) строится посредством замены Q = t^-1u(z), z = x/t, где u(z) описывается ОДУ второго порядка

Часть решений данного ОДУ выражается следующей формулой, по-лученной с использованием пакета Mathematica

Замена τ = bt, y = (b/a)x позволяет перейти от уравнения (2) к уравнению

(4)

которое имеет две группы аналитических решений. Решение уравнения (4) типа бегущей волны в явном виде описывается формулами:

где c₁, c₂, c₃ – произвольные постоянные. Автомодальное решение уравнения (4) имеет вид Q = τ^-1u(z), z = y/τ, где u(z) описывается ОДУ второго порядка

Таким образом, при выполнении ряда упрощающих условий для отдельных выработок можно найти аналитическое решение уравнения (2), либо перейти от (2) к более простой задаче решения ОДУ второго порядка. В общем же случае аналитического решения уравнения (2) построить не удаётся. Нетривиальным также является вопрос о переходе от аналитического решения для отдельной выработки (ветви) к решению на целой сети. Основные сложности при этом возникают во время учёта узловых уравнений.

Аппроксимация уравнений по методу прямых

Полудискретизированные по пространству в соответствии с методом прямых уравнения, описывающие ШВС, были получены и приведены к удобной для моделирования на ЭВМ форме В. А. Святным [1] и О. В. Молдовановой [4]. В частности, для случая, соответствующего уравнениям (1), согласно [4] полудискретизированная система уравнений принимает вид:

(5)

где _Δξ – шаг дискретизации по пространственной координате.

Система уравнений (5) имеет порядок аппроксимации O(_Δξ). С целью повышения точности аппроксимации в выражениях для α_i и β(t) значения сечений S_i целесообразно брать усреднёнными вдоль участков, аппроксимирующих часть выработки, а для вычисления γ_i сечение S_i необходимо брать равным сечению в точке, для которой строится соответствующее ОДУ. В том случае, если это узловая точка графа Г, существует несколько вариантов рационального выбора сечения S_t при вычислении γ_i. Из физических соображений S_i следует выбирать таким, каково среднее сечение на соответствующем узлу участке сочленения выработок. Если же это сечение определить не удаётся, то в качестве S_i можно брать величину, равную среднему арифметическому сечений на участках, инцидентных данному узлу.

Систему уравнений (5) можно переписать в матрично-векторном виде, используя понятие вторичной топологии.

Определение. Графом вторичной топологии G_Δξ(Г) шага дискретизации по пространству Δξ для сети Г будем называть невзвешенный граф G, полученный из исходного графа сети Г путём замены каждого ребра u простой цепью длины (l_u/Δξ)+1, где l_u – длина ребра u в графе Г, или, что равносильно, помещением l_u/Δξ дополнительных вершин на ребре u.

Если принять, что V – вершинно-рёберная матрица (0, 1, -1)- инциденций вторичного графа G_Δξ(Г), то система (5) в матрично-векторной записи будет выглядеть следующим образом:

(6)

где α = diag(α_i,i=1,m) и β = diag(β_i,i=1,m) – диагональные матрицы размер-ности m x m с элементами α_i и β_i ставящимися в соответствие ветвям графа вторичной топологии; а γ = diag(γ_i,i=1,n) – диагональная матрица размерности (n x n) с элементами γ_і, ставящимися в соответствие узлам графа вторичной топологии. Если ввести в рассмотрение матрицу

то система (6) принимает вид

(7)

где x = (Q, p)^T.

Спектр матрицы M

Перед непосредственным переходом к вопросу об устойчивости системы уравнений (7) следует рассмотреть свойства спектра матрицы M. Некоторое представление об особенностях спектра матрицы M даёт изучение характеристического полинома.

Утверждение 1. Характеристический полином матрицы M определяется выражением:

(8)

где γ(Г) – количество независимых контуров в графе Г, а матрица S = (s_ij)^m(G)_i,j=1 имеет следующие элементы

Правильность этого утверждения доказывает следующая последовательность равенств

и два очевидных тождества

в которых c_i – транспонированный i-ый столбец матрицы V.

Использование утверждения 1 позволяет точно определять спектр матрицы M для некоторых вариантов топологий, значений параметров и режимов работы ШВС. В частности, имеет место

Следствие 1. Если все элементы диагональной матрицы βdiag(|Q|) равны d, т.е. βdiag(|Q|) = dIm(G), выражение (8) переходит в

Если кроме того сечение вдоль ветвей постоянно по длине и по времени, то

и собственными числами соответственно являются значения

где λ_i(ℑ) – собственные числа лапласиана графа вторичной топологии G_Δξ(Г).

Из утверждения 1 также следует ряд фактов, отражающих связь между матрицей S и рёберным графом L(G_Δξ(Г)) графа вторичной топологии.

Следствие 2. В случае непрерывности сечения вдоль пространственной координаты по всему графу имеет место оценка

и следующее из неё предельное соотношение

Следствие 3. В случае непрерывности сечения вдоль пространственной координаты по всему графу имеет место соотношение

Для отдельных специальных классов графов и групп параметров ШВС собственные числа матрицы M могут быть точно вычислены из спектра лапласиана графа G_Δξ(Г) в соответствии со следствием 1, либо исходя из других соображений. Однако в большинстве случаев удается получить лишь некоторые неравенства для собственных чисел. Основная масса подобных соотношений получается посредством прямого применения неравенств к матрице M, известных из линейной алгебры [5, 6].

Часть результатов, полученных с использованием этого подхода, приведена в таблице 1. В неравенствах из таблицы 1 приняты следующие обозначения: m_ij – элемент матрицы M; R_i = ∑^N_j=1|m_ij| – сумма модулей элементов i-ой строки матрицы C_i = ∑^N_j=1|m_ji| – сумма модулей элементов i-ого столбца матрицы M; L = ∑_u=GΔξ(Г)l_u – суммарная длина ветвей графа ШВС Г; N = n(G) + m(G) = (2L/Δξ) – γ(Г) – 1 – размерность матрицы M.

Среди неравенств для модуля собственного числа, приведённых в таблице 1, наибольшую ценность представляют неравенство Брауэра [5] и следствие теоремы Островского [5, 6] при α = 1/2, поскольку они сильнее остальных. Кроме того, в том случае, когда Q принимает небольшое по модулю значение, следствие теоремы Островского при α = 1/2 даёт оценку, зависящую лишь от максимальной степени вершины графа ШВС pmax(Г) константы α и величины шага Δξ.

Ряд неравенств можно получить, адаптируя к специальному виду матрицы M идеи вывода известных неравенств. Так, аналог теоремы Гершгорина (Gersgorin’s theorem) [5, 6], в котором учитывается специфика матрицы M , задаётся утверждением

Утверждение 2. Все собственные числа матрицы M лежат в объединении множеств точек комплексной плоскости, задаваемых неравенствами

(9)

Годографы, отображающие области, в которых достоверно расположен спектр матрицы M согласно неравенству (9), приведены на рис.1.

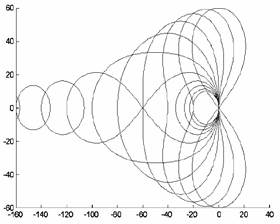
Вообще говоря, все приведенные выше неравенства довольно грубы, но для каждого из них можно указать графы ШВС или иные условия, при которых неравенство даёт хорошую оценку разброса спектра. Поэтому все известные оценки могут быть применены к матрице M, а затем из них следует выбрать наилучшую.

При построении неравенств перспективным является направление, связанное с получением оценок для спектра лапласиана графа вторичной топологий на основе информации о длине рёбер графа ШВС и значения шага по координате.

Устойчивость полудискретизированной системы по Ляпунову

Выводы об устойчивости полудискретизированной системы по Ляпунову можно сделать на основе теоремы Ляпунова об устойчивости не-линейных стационарных систем, а также утверждения 1 и его следствий. Согласно теореме Ляпунова система ОДУ, представимая в виде

(9)

в которой λ_і ∈ S_A : Re λ_і < 0 и для любого ε > 0 существует такое δ > 0, что ||g(t, x)|| ≤ ε||x|| при ||g(t, x)|| < ε||x||, t ≥ t₀, является асимптотически устойчивой. В том случае, когда в теореме Ляпунова для собственных чисел матрицы А вместо строгого выполняется нестрогое неравенство λ_і ∈ S_A : Re λ_і ≤ 0, дополнительным достаточным для асимптотической устойчивости условием является sign х_i (t) = -sign g(t, x_i(t)). В свою очередь система (7) представима в виде (9) с

(10)

откуда следует

Утверждение 3. Для асимптотической устойчивости по Ляпунову системы ОДУ (7), полученной из (1) в результате аппроксимации по методу прямых, достаточно, чтобы матрица S совпадала с лапласианом рёберного графа вторичной топологии ℑ(L(G_Δξ(Г))).

Комбинируя данное утверждение со следствиями 1 и 2, получаем

Следствие 4. В случае постоянства по длине и по времени сечения вдоль ветвей система ОДУ (7) является асимптотически устойчивой по Ляпунову.

Следствие 5. В пределе при Δξ → 0 система ОДУ (7) асимптотически устойчива по Ляпунову.

Устойчивость явных и неявных методов

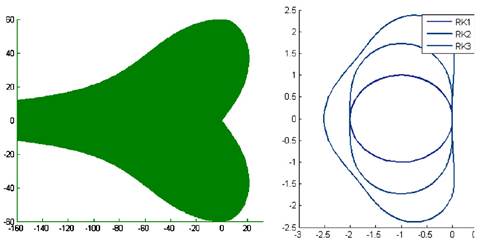
Утверждения 1 и 2 с их следствиями, а также неравенства из таблицы 1 позволяют задать условия, накладываемые на величину шага по времени, которые обеспечивают устойчивость численных методов решения системы ОДУ (7). Порядок построения таких условий следующий. Для заданной системы ДУЧП, интервала изменения значений потока Q ∈ [0, Q_max] и шага дискретизации по пространству Δξ на основе выводов из пункта 4 статьи строится система неравенств, которые задают возможный разброс спектра. Далее необходимо воспользоваться условием устойчивости для выбранного численного метода, и путём изменения шага по времени достичь полного вхождения области достоверного расположения спектра системы в область устойчивости метода.

Выводы

В данной работе приведены аналитические решения ДУЧП, описывающих движение воздуха в отдельной выработке, для случая постоянства сопротивления и поперечного сечения вдоль выработки. На основе классических неравенств линейной алгебры получен ряд утверждений о границах устойчивости численных решателей ДУЧП для моделирования динамики воздушного потока в сети, состоящей из нескольких выработок. Также приведена методика выбора шага по времени, применение которой гарантирует достижение сходимости численного метода моделирования движения воздуха в ШВС.

Литература

1. Абрамов Ф. А., Фельдман Л. П., Святный В. А. Моделирование динамических процессов рудничной аэрологии. – Киев: Наук. думка, 1981. – 284 с.
2. Святный В. А. Моделирование аэрогазодинамических процессов и разработка систем управления проветриванием угольных шахт: дис. на соискание науч. степени док. техн. наук: спец. 05.13.07 "Автоматизация технологических процессов и производств (промышленность)" / В. А. Святный; ДПИ. – Донецк, 1985. – 440 с. – Библиогр.: с. 420-440.
3. Полянин А. Д., Зайцев В. Ф. Справочник по нелинейным уравнениям математической физики: Точные решения. – М.: Физматлит, 2002. – С. 147-148 (3.3.5.1-2), С.154 (3.4.2.3); С.157 (3.4.2.13); С.158(3.4.2.14).
4. Молдованова О. В. Способы организации параллельных вычислений в задачах математического моделирования шахтных вентиляционных сетей : дис. на соискание науч. степени канд. техн. наук: спец. 01.05.02 "Математическое моделирование и численные методы" / О. В. Молдованова; ДонНТУ. – Донецк, 2008. – 140 с. – Библиогр.: с. 120-140.
5. Маркус М., Минк Х. Обзор по теории матриц и матричных неравенств [Текст] / Пер. с англ., под ред. В.Б. Лидского. – 2-е изд., стер. Москва: Эдиториал УРСС, 2004. – 232 с.
6. Гантмахер Ф.Р. Теория матриц [Текст] / Ф. Р. Гантмахер. – 5-е изд. – Москва: Физматлит, 2004. – 559 с. – Библиогр.: с.539-554(302 назв.). Предм. указ.: с.555-559 . – ISBN 5-9221-0524-8
7. Цветкович Д., Дуб М., Захс X. Спектры графов. Теория и применение / Пер. с англ. канд. физ.-мат. наук В. В. Строка; Под ред. акад. АН УССР В. С. Королюка. – Киев : Наук. думка. Ред. физ.-мат. лит., 1984. – 384 с. – Ил. 44. Библиогр.: с. 338 – 372.
8. Haemers W.H. Matrices and Graphs // In: Handbook of Linear Algebra (Discrete Mathematics and Its Applications) / Ed. by Hogben L. – Chap-man & Hall/CRC, 2006-11-02. – Ch. 28. – P.440-453. – ISBN-10 / ASIN: 1584885106; ISBN-13 / EAN: 9781584885108.
9. Doob M. Spectral Graph Theory // In: Handbook of Graph Theory (Discrete Mathematics and Its Applications) / Ed. by Gross J.L., Yellen J. – Ch.6.5 – CRC, 2003-12-29. – P. 557-574. – ISBN-10 / ASIN: 1584880902; ISBN-13 / EAN: 9781584880905.