Введение
Комбинаторные алгоритмы уже давно играют решающую роль в параллельных вычислений. Распределение разреженной матрицы и векторов среди процессоров является важной проблемой в разреженных матричных вычислений. Мы рассмотрим граф, двудольный граф, и модели гиперграфов для обеих 1D (строки или столбца) распределений и 2D распределений. Разметка гиперграфа является очень ценным инструментом. Для представления результатов мы используем параллельные разметки из инструментария Zoltan, который способен эффективно разбить очень большие наборы данных (матрицы).
Основной текст статьи
Распределение нагрузки между процессорами является важной проблемой в параллельных научных вычислениях. Наша цель — минимизировать стоимость связи при сохранении баланса приблизительное нагрузки. Эта проблема часто моделируется как граф (или гиперграф) разбиение, где вершины вычислительные задачи и края представляют зависимости данных.
Во многих численных алгоритмах мы сосредотачиваем внимание на общем ядре: умножение из разреженной матрицы на вектор. Эта операция, например, является вычислительно наиболее дорогостоящей частью итерационных методов для линейных систем. Большинство зависимостей данных в научных расчетов могут быть смоделированы в виде графиков или гиперграфах, которые снова могут быть представлены как матрицы. Вопрос в том, как распределить ненулевую матрицу записи среди процессоров. Разряженные случаи являются достаточно сложными и представляют собой богатый источник комбинаторных задач. Эта проблема была подробно изучены в [1] и [2].
Одномерное (1D) разложение матрицы является наиболее распространенным и представляет собой либо матричные строки, либо столбцы. Для перемножения матрицы-вектора с 1D распространения необходима связь, показаная на рисунке 1. Эта структура может быть смоделированы в виде графа, двудольного графа, или гиперграфа, обобщенного графа. Модель гиперграф точно отображает объем связи и, следовательно, превосходит стандартную модель графа. Тем не менее, модель двудольного графа также может быть использована. У модели двудольного и гиперграфа есть еще одно преимущество — они работают на несимметричных матрицах в то время как модель графа предполагает симметричную. Связность часто может быть уменьшена с помощью более сложных 2D распределений, что опять приведет к новому графу и модели гиперграфа.
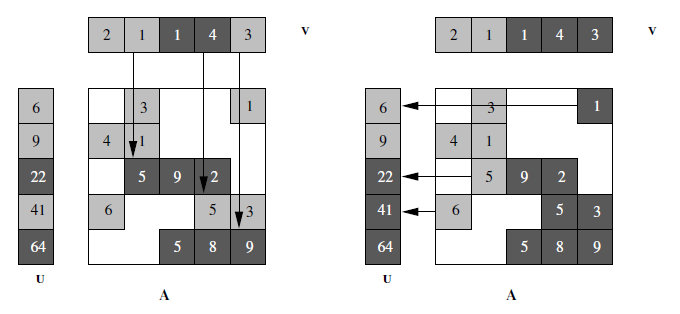
Рисунок 1 — Распределение разреженной матрицы по ряду (слева) и колонке (справа) для умножение u = Av
Есть только два процессора, обозначенные темным и светлым участками. Связь между ними показаны стрелками.
Инструментарий Zoltan был разработан в Sandia National Labs и содержит широкий ассортимент разбиений и методов балансировки нагрузки, в том числе, разметку параллельного гиперграфа [3]. Результаты трех различных областей применения показаны далее:
- код Tramonto DFT для моделирования наноразмерных жидкости,
- моделирования электронных схем,
- код DNA.
Результатом для всех областей является структурная симметричная разреженная матрица. С помощью разбиения графа (ParMetis) и разбиения гиперграфа (Zoltan) мы вычисляем необходимое разбиение. Уменьшение связности зависит от структуры матрицы. Фактический, время выполнения также уменьшается, но менее резко, чем указывает связность. Прирост производительности для матрицы–вектора ядра в примерах TRAMONTO и Xyce был с 13% до 18%, соответственно, по сравнению с разбиением графов на 64-процессорном кластере.
Список использованной литературы
1. U. Catalyurek and C. Aykanat. Hypergraph—partitioning—based decomposition for parallel sparse—matrix vector multiplication. IEEE Trans.
Parallel Dist. Systems, 10(7):673—693, 1999.
2. R. H. Bisseling. Parallel Scientific Computing: A structured approach using BSP and MPI. Oxford University Press, 2004.
3. K.D. Devine, E.G. Boman, R.T. Heaphy, R.H. Bisseling, and U.V. Catalyurek. Parallel hypergraph partitioning for scientific computing. In Proc. of IPDPS’06. IEEE, 2006. To appear.