УДК 001.1

Исследование алгоритмов разбиения чисел на простые множители

Братуха М.А., Мирошкин А.Н., Белецкий О.В, Мальчева Р.В.

ГВУЗ Донецкий национальный технический университет, г. Донецк, Украина

astr0n@ukr.net

Аннотация

Рассмотрены способы разбиения чисел на множители, разработан обратный алгоритм – формирование заданного числа из простых множителей. Так же разработана программа анализа трудоёмкости некоторых рассмотренных алгоритмов с точки зрения практического применения на микроконтроллерах.

Введение

Простые числа – это ключ к разрешению многих математических проблем, они также играют большую роль в криптографии (шифровании), благодаря чему интересуют не только математиков, но и военных, разведку, поскольку данные в такой области всегда передаются в зашифрованном виде. Простое число – это то число, которое делится без остатка только на единицу и само на себя. Так, к простым числам относятся: 2, 3, 5, 7, 11, 13 и так далее. Так же не менее важной проблемой является факторизация.

Факторизация натурального числа – это разложение натурального числа на простые множители. С точки трудоёмкости, предположительно, факторизация является более сложной задачей, нежели нахождение простого числа, что повлекло за собой применение этого принципа в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA.

Задача данного исследования – это рассмотреть существующую алгоритмы факторизации натуральных чисел и привести пример практического применения такой задачи в сфере специальных ЭВМ (микроконтроллеров).

1 Проблема поиска простых чисел

В наше время существует достаточное количество алгоритмов поиска простых чисел, например, самые известные из них: решето Эратосфена, решето Аткина, проверка перебором делителя и так далее. Однако все эти алгоритмы является достаточно трудоёмкими, и при больших числах они являются неэффективными. Рассмотрим некоторые из них в отдельности.

Проверка перебором делителя

В данном алгоритме число, отправленное на проверку простоты делиться на все числа от 2 до корня из n. Время работы такого алгоритма составляет порядка О(n1/2), то есть растёт экспоненциально относительно битовой длины n. Пример реализации такой алгоритма представлено ниже:

bool IsPrime(long long n)
{
	if (n == 1) // 1 - не простое число
		return false; // перебираем возможные делители от 2 до sqrt(n)
	for (d = 2; d * d <= n; d++) // если разделилось нацело, то составное
	{
		if (n % d == 0) return false; // если нет нетривиальных делителей, то простое
	}
	return true;
}

Решето Эратосфена

Древнегреческий математик Эратосфен предложил следующий алгоритм для нахождения всех простых, не превосходящих данного числа n: берётся массив S длины n и заполняется единицами (помечается как невычеркнутые), затем последовательно просматриваются элементы S[k], начиная с k = 2. Если S[k] = 1, то заполняется нулями (вычеркнем или высеем) все последующие ячейки, номера которых кратны k. В результате получается массив, в котором ячейки содержат 1 тогда и только тогда, когда номер ячейки – простое число.

Много времени можно сэкономить, если заметить, что, поскольку у составного числа, меньшего n, по крайней мере, один из делителей не превосходит , процесс высевания достаточно закончить на .

Эффективность решета Эратосфена является достаточно большой, поскольку внутренний цикл не содержит условных переходов, а также «тяжёлых» операций вроде деления и умножения, что очень хорошо видно из листинга ниже:

bool* sieve(long long n)
{
	bool S[n];
	S[1] = false; // false - не простое число
	// заполняем решето единицами
	for (k = 2; k < = n; k++) S[k] = true;
	for (k = 2; k * k < = n; k++)
	{ // если k - простое (не вычеркнуто)
		if(S[k] == true)
		{ // то вычеркиваются кратные k
			for(l=k*k; l<=n; l+=k) {
				S[l] = false;
			}
		}
	}
	return S;
}

Сложность алгоритма будет такая: для первого действия – n/2, для второго – n/3, для третьего – n/4 и так далее. Таким образом для решета Эратосфена необходимо О(n log log n) операций.

2 Алгоритмы факторизации натуральных чисел

Согласно основной теореме арифметики любое положительное целое число больше единицы может быть уникально записано в следующей главной форме разложения на множители, где p1, p2, ..., pk – простые числа и e1, e2, ..., ek – положительные целые числа.

Самый простой и наименее эффективный алгоритм – метод разложения на множители проверкой делением. Для этого просто пробуются все положительные целые числа начиная с 2, для того чтобы найти одно, которое делит n. После обсуждения решета Эратосфена известно, что если n составное, то делитель будет простым числом p ≤ √n. Однако такой алгоритм можно упростить, если делать проверка не на все числа, а только на простые.

Более совершенный метод – это метод Ферма, который основан на факте, что если мы можем найти x и y, такие, что n = x2 – y2, тогда мы имеем n = x2 – y2 = x * b, при a = (x + y) и b = (x – y). Метод сводится к попытке найти два целых числа a и b, близкие друг к другу. Начиная с наименьшего целого числа, большего, чем x = √n. Потом ищется другое целое число y, такое, чтобы выполнялось уравнение y2 = x2 – n. В каждой итерации должно быть рассмотрено, является ли результат x2 – n полным квадратом. Если находится такое значение для y, то вычисляется a и b, а затем выход из цикла. Если это не делается, то проводится другая итерация.

Заметим, что метод не обязательно находит разложение на простые числа (каноническое разложение); алгоритм должен быть повторен рекурсивно для каждого из значений a и b, пока не будут найдены сомножители в виде простых чисел.

В 1974 г. Джон Поллард разработал метод, который находит разложение числа p на простые числа. Метод основан на условии, что p–1 не имеет сомножителя, большего, чем заранее определенное значение B, называемое границей. Алгоритм Полларда показывает, что в этом случае p = НОД(2B! – 1, n).

Нужно заметить, что этот метод требует сделать B–1 операций возведения в степень (a = a e mod n). Метод также использует вычисления НОД, который требует n3 операций. Точно можно сказать, что сложность – так или иначе больше, чем O(B) или O(2n), где nb – число битов в B. Другая проблема – этот алгоритм может заканчиваться сигналом об ошибке. Вероятность успеха очень мала, если B имеет значение, не очень близкое к величине √n.

Померанс изобрел метод разложения на множители, называемый методом квадратичного решета. Метод применяет процедуру просеивания, чтобы найти значение x2mod n. Метод используется, чтобы разложить на множители целые числа с более чем 100 цифрами. Его сложность – О(ec), где C ≈ 2(ln n ln ln n)1/2. Стоит отметить, что это – субпотенциальная сложность.

Эндрик Ленстра и Арджин Ленстра изобрели метод разложения на множители и назвали его метод решета поля чисел. Метод использует процедуру просеивания в алгебраической кольцевой структуре к x2 ≡ y2 mod n. Показано, что этот метод быстрее для разложения чисел с более чем 120 десятичными цифрами. Его сложность – O(eС) где C ≈ (ln n)1/3 (ln ln n)2/3. Стоит обратить внимание, что это – также субпоказательная сложность.

3 Факторизации на микроконтроллере

В качестве объекта исследования был выбран микроконтроллер i8051 (КМ1816ВЕ51). Данный микроконтроллер имеет 4 режима работы таймера (счётчика). В одном из режимов (второй) таймерный регистр имеет разрядность 16 бит, что позволяет вести счёт до 65535, то есть это позволяет задавать лишь малые интервалы времени. Для задания больших интервалов используются дополнительные ячейки памяти, размерностью в 1 байт, однако их использование может привести к небольшим временным искажениям, что не приемлемо в системах реального времени. Поэтому, использование дополнительных ячеек памяти нужно свести к минимуму, а это напрямую зависит от правильности разбиения исходного числа – его необходимо разбить таким образом, чтобы возможности таймерного регистра использовались в полной мере, то есть были как можно ближе к значение 65535. Значение же каждой ячейки памяти не превышает 255.

Как раз для оптимальности разбиения исходного числа и были применены некоторые вышерассмотренные алгоритмы.

Метод поиска оптимальных делителей для любого из алгоритмов будет таким:

1) Найти делитель, максимально приближенный к значению 65535;

2) Найти оставшиеся делители, которые будут иметь значение, не превышающее 255.

В качестве первого алгоритма тестирования был выбран самый очевидный – это перебор всех возможных делителей исходного числа.

В качестве второго (показательного) алгоритма был выбран алгоритм разложения исходного числа на простые множителе с последующим формированием необходимых чисел для таймерного регистра и ячеек памяти – 65535 и 255, соответственно. Поскольку для этого алгоритма необходимо знать простые числа вплоть до корня из исходного числа, поэтому нужно каким-либо образом их найти. Можно, конечно, использовать один из вышерассмотренных алгоритмов поиска простых чисел, однако это значительно повысит трудоёмкость алгоритма в целом, что в результате можно сравнять этот алгоритм с «очевидным». Исходя из этого, был решено взять уже известные простые числа до числа 3571 и использовать их, вместо поиска. Такой подход позволит находить делители числа вплоть до 12 миллионов, а в случае надобности этот список можно расширить.

Для тестирования обоих алгоритмов была разработана программа на языке C++, которая делала временные замеры выполнения алгоритмов. В качестве инструментов измерения таких интервалов выступала WinAPI-функция QueryPerformanceCounter(), которая возвращает значение счётчика, набежавшие с момента старта ОС.

На рисунке 1 представлены временные замеры для первого алгоритма.

График зависимости времени выполнения алгоритма от заданного числа для алгоритма перебора всех делителей
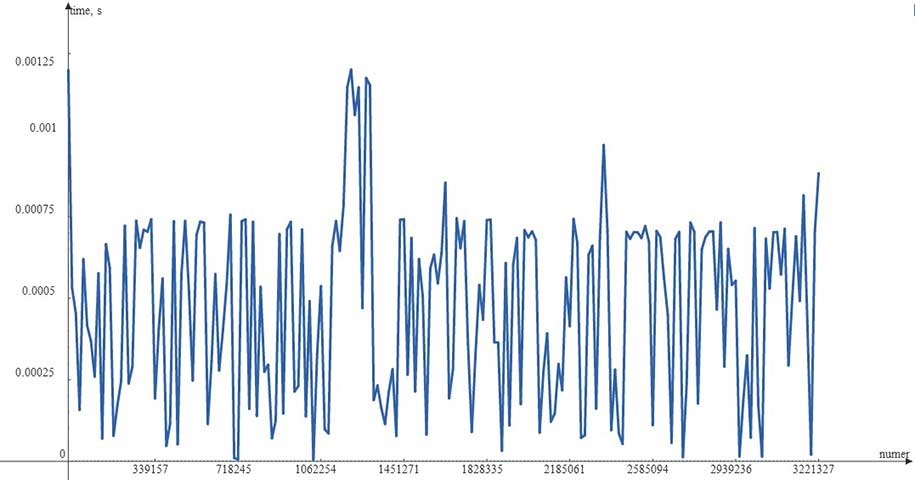
Рисунок 1 – График зависимости времени выполнения алгоритма от заданного числа для алгоритма перебора всех делителей

Из рисунка видно, что время выполнения данного алгоритма не превышает 1,25 мс. На рисунке 2 изображён такой же график зависимости, только для алгоритма разложения чисел на простые множители и последующего формирования оптимальных делителей для потребностей микроконтроллера. Из рисунка видно, что время выполнения данного алгоритма не превышает 0,3 мс, что в ~4 раза меньше, чем первого алгоритма. Так же полученный график является более плавным, что свидетельствует о большей постоянности алгоритма при различных числах, чем у первого алгоритма, тем боле, что большая часть чисел разбивается за менее чем 0,1 мс.

График зависимости времени выполнения алгоритма от заданного числа для алгоритма перебора всех делителей
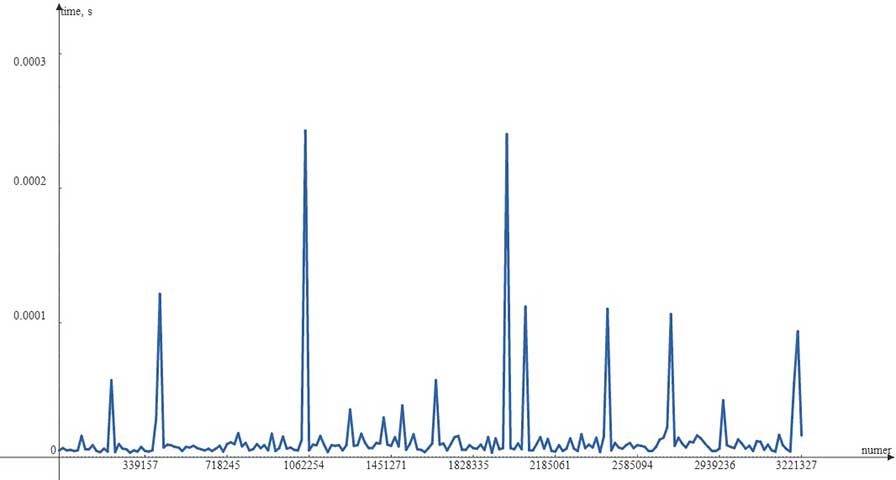
Рисунок 2 – График зависимости времени выполнения алгоритма от заданного числа для алгоритма перебора всех делителей

Выводы

По результатам работы программы видно, что от выбора алгоритма поиска оптимальных множителей зависит время его выполнения, и что порой самый очевидный способ не является самым эффективным. Поскольку при рассмотрении «самого худшего варианта» использовались константные значения простых чисел, вместо их поиска, то, конечно же, при реализации такого алгоритма на микроконтроллере стоит заменить такой способ на метод Эратсофена, что увеличит время выполнения алгоритма, но не существенно. Лучшего всего заменить такой алгоритм на более совершенный – метод Ферма или любой другой, который требует минимум аппаратных ресурсов.

Реализация любого из алгоритмов позволит вводить пользователю (буквально) любое число, которое будет разбиваться на части и сохранятся в регистре таймера и дополнительных ячейках памяти самым оптимальным образом, что позволит сделать погрешность при временных измерениях – минимальной.

Литература

1. Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. - 384 с.

2. Нестеренко Ю. В. Теория чисел : учебник для студ. высш. учеб. заведений / Ю. В. Нестеренко. — М.: Издательский центр «Академия», 2008. - 272 с.

3. Сташин В.В. Проектирование цифровых устройств на однокристальных микроконтроллерах/ В.В. Сташин, А.В. Урусов, О.Ф. Мологонцева. – М.: Энергоатомиздат, 1990 – 224 с.

4. Описание алгоритмов факторизации натуральных чисел [электронный ресурс]. – Режим доступа: http://www.intuit.ru/.

5. Практические примеры алгоритмов поиска простых чисел и факторизации [электронный ресурс]. – Режим доступа: http://habrahabr.ru/.