Аннотация
Назаренко Д.А., Чередникова О.Ю. – Математическое моделирование переходных процессов в шахтной вентиляционной сети
Общая постановка проблемы
Шахтная вентиляционная сеть (ШВС) – это сложный сетевой объект, имеющий от 500 до 1500 ветвей. В задачах анализа воздухораспределения в ШВС используются различные программные комплексы, однако они обеспечивают решение лишь для установившегося режима. В настоящее время становится актуальной также задача моделирования динамики воздушных потоков, решение которой требуется при реализации различных алгоритмов управления воздухораспределением.
Пусть анализируемая сеть имеет ветвей и узлов. Тогда для нее должно быть составлено узловых и контурных уравнений. Узловые уравнения
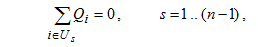
где Qi – расход воздуха в i–ой ветви, инцидентной узлу Us.
Потери энергии в ветви с учетом переходного процесса:
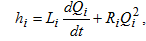
где Li – инерционность потока в i–ой ветви; Ri – активное сопротивление ветви.
Контурные уравнения
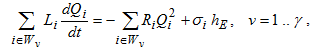
где HE – напор источника энергии (вентилятора главного проветривания (ВГП)),
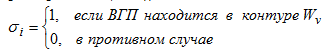
На рис.1 приведена упрощенная схема сетевого объекта (m=12, n=9, y=4). Ветви 11 и 12 – фиктивные, замыкающие воздушные потоки ШВС через атмосферу. Пунктиром показаны главные ветви, последовательное включение которых обеспечивает независимость контурных уравнений. Нумерация ветвей в сети произведена таким образом, чтобы главные ветви получили последовательные номера 1...y.
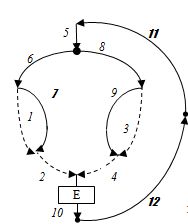
Рисунок 1 – Схема сетевого объекта
Численное интегрирование систем (1) и (2) показало, что процесс решения в данном случае имеет неустойчивый характер. В связи с этим была поставлена задача разработать такую модификацию математического описания ШВС, которая обеспечивала бы устойчивость численного решения.
Заменив в левой части системы (2) потоки Q5..Q12 на главные потоки Q1..Q4 и проинтегрировав левую и правую части уравнений, после преобразований получим
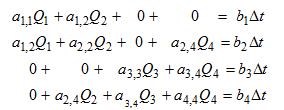
Здесь b1..b4 – правые части соответствующих уравнений системы (2).
Запишем в явном виде матрицу контуров С, в которой номер строки определяет номер контура, а номер столбца – номер ветви.
 (3)
(3)
Значения коэффициентов ai,j и свободных членов программа вычисляет автоматически по следующим формулам:
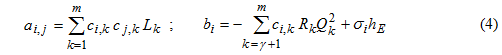
Система (3) – это модификация системы обыкновенных дифференциальных уравнений первого порядка. Решение системы (3) на каждом шаге сводится к решению системы линейных алгебраических уравнений, определяемой матрицей коэффициентов А и вектором свободных членов B с использованием системы узловых уравнений при вычислении элементов bi.
Возможные способы решения системы (3): метод Гаусса, обратная матрица, метод Зейделя.
Матрицы коэффициентов в узловых и контурных уравнениях являются сильно разреженными. Поэтому целесообразно сохранять в памяти лишь ненулевые элементы этих матриц. Поскольку метод Зейделя, в отличие от метода Гаусса и обратной матрицы, не добавляет новые элементы в процессе своей работы, то он является предпочтительным, если при этом выполняются условия устойчивости решения. Достаточным критерием устойчивости решения является выполнение отношения:
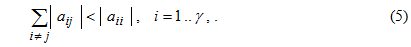
Анализ матрицы коэффициентов (3) и формулы (5) показывает, что такое условие в матрице А сетевого объекта выполняется.
К настоящему времени выполнены численные эксперименты для сравнительно небольшой сети. Программа моделирования реализована на языке Турбо Паскаль, построение максимального дерева, формирование узловых и контурных уравнений и их преобразование выполняются вручную. В дальнейшем запланировано переход на систему программирования Delphi, подготовка сети, имеющей не менее 1000 ветвей, и автоматизация подготовительных операций.
Список использованной литературы
1. Святный В.А. Решение задач расчета воздухораспределения в шахтной вентиляционной сети методом установления // Известия вузов. Горный журнал. – 1979, №1. – С.50–59.
2. Бахвалов Н.С. Численные методы. –М.: Наука, 1973. – 632 c.