Анализ различных активационных функций с помощью нейронных сетей обратного распространения ошибки
Автор: P. SIBI, S. ALLWYN JONES, P. SIDDARTH
Перевод:Семенова А.П.
Источник: Journal of Theoretical and Applied Information Technology, 31 January 2013. Vol. 47 No. 3 p. 1264–1268
Аннотация
P. SIBI, S. ALLWYN JONES, P. SIDDARTH. Анализ различных активационных функций с помощью нейронных сетей обратного распространения ошибки. Алгоритм обратного распространения ошибки позволяет передавать многослойной нейронной сети прямого распространения для обучения входные (выходные) преобразования из обучающих выборок. Сети обратного распространения адаптируются, чтобы изучить отношения между набором образцов, и применить те же отношения к новым входным образцам. Сеть должна обращать внимание на особенности произвольного входного потока. Активационная функция используется для преобразования уровня активации нейрона в выходной сигнал. Существует ряд общих активационных функций при использовании искусственных нейронных сетей (ANN). В статье выполнен анализ различных активационных функций и выделена одна из них в качестве эталона. Цель – определить оптимальную активационную функцию для рассматриваемой проблемы.
Ключевые слова: искусственная нейронная сеть, сеть обратного распространения ошибки, активационная функция.
1. Введение
Нейронная сеть называется сетью отображения, если она может вычислить некоторые функциональные отношения между своим входом и выходом. Например, если на вход сети поступает значение угла, а на выход – косинус угла, сеть выполняет преобразование σ → cos(σ). Предположим, что у нас есть набор пар вектора P (x1, y1),(x2, y2)...(xp, yp), в которых приведены примеры функционального преобразования y = μ(х): x ∈ RN,у ∈ RM. Мы должны обучить сеть так, чтобы она рассматривала приближение о = у' = μ'(х). Следует отметить, что обучение нейронной сети состоит в нахождении приближенного набора весов.
Приближения функций из набора входных-выходных пар применяют в многочисленных научных и инженерных программах. Многослойные нейронные сети прямого распространения были предложены в качестве инструмента для нелинейной аппроксимации функции[1], [2], [3]. Параметрические модели, представленные такими сетями являются нелинейным. Алгоритм обратного распространения ошибки – это широко используемый алгоритм для обучения многослойных сетей путем распространения ошибки с помощью вариационного исчисления [4], [5]. Он многократно настраивает параметры сети, чтобы минимизировать сумму квадратов ошибок аппроксимации с помощью метода градиентного спуска. Из-за чрезвычайно нелинейной моделирующей мощности таких сетей, обучающая функция может интерполировать все обучающие точки. Когда подаются зашумленные данные, обучающая функция может резко колебаться между точками данных. Поэтому аппроксимация функций из зашумленных данных явно нежелательна.
2. Механизм сети с обратным распространением ошибки
Передадим входной вектор на входной слой. Входным вектором назовем Xp = (xp1, xp2,...,xpN)t. Вычислим входные значения сети в скрытом слое уровня:

где netpjh – вход сети в скрытом слое, wjih – вес связи с i-м входным узлом, σjh – это переменная, показывающая смешение узла «h» на скрытом слое.
Рассчитаем значения на выходе из скрытого слоя: ipj = fjh(netpjh), где ipj – это выход из скрытого слоя, а fjh – активационная функция.
Перейдем к выходному слою. Рассчитаем входные значения узла для каждого блока:

где netpko – входные значения сети для выходного слоя, wjio – вес в связи с j-м скрытым узлом, σko – это переменная, показывающая смешение узла «o» на скрытом слое.
Посчитаем результат: Opk = fko(netpko), где Opk – выходное значение выходного слоя.
Рассчитаем ошибки вычисления для выходных узлов: δpko = (ypk - Opk)fjo'(netpko), где δpko – ошибка на выходе каждого узла, δpko = (ypk - Opk), где ypk – ожидаемая ошибка, а Opk) – фактическая ошибка.
Рассчитаем ошибку для скрытых узлов:

где δpjh – ошибка в каждом скрытом узле. Обратите внимание, что ошибки в скрытых узлах вычисляются перед передачей обновленных значений весов на выходной слой.
Обновление весов:
а) выходного слоя: wkjo(t+1) = wkjo(t) + ηδpkoipj;
б) скрытого слоя: wjih(t+1) = wjih(t) + ηδpjhxi,
где η – параметр скорости обучения. Порядок обновления весов каждого узла на одном слое не важен.
Доказано, что вычисление погрешности  является мерой качества обучения сети.
является мерой качества обучения сети.
Когда ошибка становится относительно небольшой для каждой пары обучающего вектора, обучение сети может быть прекращено [6]. Пример сети с обратным распространением ошибки приведен на рисунке 1.
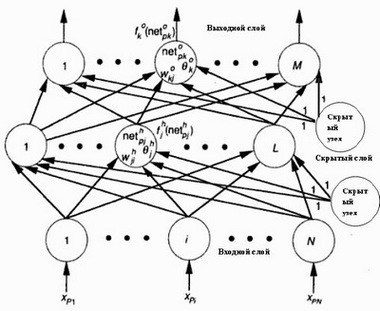
Рисунок 1 – Cеть с обратным распространением ошибки
3.Типы активационных функций
Каждая нейронная модель состоит из обрабатывающего элемента с синаптическими входными соединениями и одним выходом. Сигнал входного потока нейрона считается однонаправленным [7]. Сигнал входного потока нейрона определяется следующим отношением:  и приведен на рисунке 2.
и приведен на рисунке 2.

Рисунок 2 – Сигнал входного потока нейрона
Функции описаны такими параметрами:
– вход активационной функции х;
– выход у;
– скорость роста s;
– отклонение d.
3.1. Линейная активационная функция
Областью определения линейной активационной функции является действительный диапазон чисел: y = x*s, d = 1*s. Не может быть использована в фиксированной точке.
3.2. Сигмоидная активационная функция
В сигмоидной функции будут только положительные числа из диапазона между 0 и 1. Сигмоидная активационная функция наиболее полезна для обучающих данных, которые также находятся в диапазоне между 0 и 1. Это одна из наиболее используемых активационных функций. Диапазон: 0 < y < 1, y = 1/(1 + exp(-2*s*x)), d = 2*s*y*(1 - y)
3.3. Ступенчатая сигмоидная активационная функция
Ступенчатая сигмоидная активационная функция является кусочно-линейной аппроксимацией обычной сигмоидной функции с выходными значениями между нулем и единицей. Она быстрее чем сигмоидная, но менее точная.
3.4. Симметричная сигмоидная активационная функция
Симметричная сигмоидная активационная функция является сигмоидной функцией гиперболического тангенса с выходными значениями от -1 до 1. Это одна из наиболее используемых активационных функций. Диапоазон: -1 < у < 1, y = tanh(s*x) = 2/(1 + exp(-2*s*x)) - 1, d = s*(1 - (y*y)), где tanh – функция гиперболического тангенса.
3.5. Ступенчатая симметричная сигмоидная активационная функция
Ступенчатая симметричная сигмоидная активационная функция является кусочно-линейной аппроксимацией сигмоидной функции гиперболического тангенса с выходными значениями от -1 до 1. Она быстрее чем симметричная сигмоидная активационная функция, но менее точная.
3.6. Активационная функция Гаусса
Активационная функция Гаусса может быть использована при необходимости более точного управления диапазоном активации. Область определения – от 0 до 1: 0 когда х равен бесконечности, 1 когда х = 0. Диапазон: 0 < y < 1, y = exp(-x*s*x*s), d = -1*x*s*y*s.
3.7. Симметричная активационная функция Гаусса
Симметричная активационная функция Гаусса может использоваться когда необходимо очень точное управление диапазоном активации. Область определения: от -1 до 1: -1 когда х равен минус бесконечность, 1 когда х = 0, 0 когда х равен бесконечности. Диапазон: -1 < y < 1, y = exp(-x*s*x*s)*2 - 1, d = -2*x*s*(y + 1)*s.
3.8. Активационная функция Эллиота
Активационная функция Эллиота является более быстрой аппроксимацией активационной функции гиперболического тангенса. Область определения: от 0 до 1. Диапазон: 0 < y < 1, y = ((x*s)/2)/(1 + |x*s|) + 0.5, d = s*1/(2*(1 + |x*s|)*(1 + |x*s|)).
3.9. Симметричная активационная функция Эллиота
Симметричная активационная функция Эллиота является более быстрой аппроксимацией сигмоидной активационной функции. Область определения: от -1 до 1. Диапазон: -1 < y < 1, y = ((x*s)/2)/(1 + |x*s|), d = s*1/((1 + |x*s|)*(1 + |x*s|)).
3.10. Кусочно-линейная активационная функция
Эта активационная функция называется также линейной функцией насыщения и может иметь двоичный или биполярный диапазон для ограничения перегрузки выходных данных. Область определения: от 0 до 1. Диапазон: 0 < y < 1, y = x*s, d = 1*s.
3.11. Симметричная кусочно-линейная активационная функция
Тоже, что и кусочно-линейная активационная функция, но с областью определения от -1 до 1. Диапазон: -1 < y < 1, y = x*s, d = 1*s.
4. Результаты эксперимента
Был выбраны данные для оценки активации сети. Был разработан специальный тренажер для тестирования активационной функции с помощью открытой библиотеки FANN (Fast Artifical Neural Network – быстрая искусственная нейронная сеть). Тренажер был написан на языке Python с привязкой, которая была осуществлена с помощью SWIG (Simplified Wrapper Interface Generator), к языку библиотеки FANN. В качестве данных, выбранных для анализа использовались данные о грибах. Проблема классификации грибов состоит в том, что на основании видимых отличий необходимо определить является ли гриб съедобным или ядовитым. 22 входных объекта были преобразованы в 125 бинарных атрибута. Особенности входных данных приведены в таблице 1.
Таблица 1 – Входные значения
| Особенность | Значение |
| форма шапки | колокол / коническая / выпуклая / плоская / колоковидная / впалая |
| поверхность шапки | волокнистая / с выемками / чешуйчатая / гладкая |
| цвет шапки | коричневый / темно-желтый / светло-коричневый / серый / зеленый / розовый / фиолетовый / красный / белый / желтый |
| повреждения | да / нет |
| запах | миндальный / анисовый / креозотный / рыбный / вонючий / заплесневелый / нет / пикантный / пряный |
| юбка | прикреплена / опускающаяся/ свободная / зубчатая |
| расстояние между шапкой и юбкой | близко / прижата / далеко |
| размер юбки | широкая / узкая |
| цвет юбки | черный / коричневый / темно-желтый / шоколадный / серый / зеленый / оранжевый / розовый / фиолетовый / красный / белый / желтый |
| форма стебля | увеличенная / суженная |
| корень стебля | луковичный / клубневый / чашевидный / ровный / нитевидный / коренистый / отсутствует |
| стебель выше кольца | волокнистый / чешуйчатый / шелковистый / гладкий |
| стебель ниже кольца | волокнистый / чешуйчатый / шелковистый / гладкий/td> |
| цвет стебля выше кольца | коричневый / темно-желтый / светло-коричневый / серый / оранжевый / розовый / красный / белый / желтый |
| цвет стебля ниже кольца | коричневый / темно-желтый / светло-коричневый / серый / оранжевый / розовый / красный / белый / желтый |
| тип покрывала | частное / общее |
| цвет покрывала | коричневый / оранжевый / белый / желтый |
| количество колец | нет / одно / два |
| тип кольца | нитевидный / временный / выпуклый / большой / нет / висячий / обшивка / поясной |
| цвет споры | черный / коричневый / темно-желтый / шоколад / зеленый / оранжевый / фиолетовый / белый / желтый |
| популяция | богатая / групповая / многочисленная / разрозненная / небольшое количество / одиночная |
| среда обитания | луг / листья / поляна / дорожки / город / свалка / лес |
5. Оценка эффективности
При обучении по данным о грибах ожидаемая ошибка составила 0,0999. для обучения использовался алгоритм RPROP (Resilient Propagation – плотное распространение). В качестве коэффициента увеличения и коэффициента уменьшения для алгоритма были выбраны оптимальные значения равные 1,5 и 0,2 соответственно. В качестве δmin выбрано значение 0, а для δmax = 50. Количество скрытых слоев равно 3, по 4, 5 и 5 нейронов на слое соответственно. Полученный результат моделирования приведен в таблице 2.
Таблица 2 – Результат моделирования
| Оценка данных о грибах | |||
| Активационная функция | Общее количество эпох | Ошибка на последней эпохе | Количество неудач на последней эпохе |
| Линейная | 47 | 0,006335672 | 21 |
| Сигмоидная | 30 | 0,0003930641 | 4 |
| Ступенчатая сигмоидная | 41 | 0,0007385524 | 6 |
| Симметричная ступенчатая сигмоидная | 26 | 0,0095451726 | 50 |
| Гаусс | 50 | 0,0079952301 | 24 |
| Симметричная Гаусса | 21 | 0,0063603432 | 8 |
| Эллиот | 22 | 0,0096499957 | 6 |
| Симметричная Эллиота | 42 | 0,0090665855 | 125 |
| Кусочно-линейная | 71 | 0,009539031 | 90 |
| Симметричная кусочно-линейная | 28 | 0,0084868055 | 110 |
| Симметрический синус | 33 | 0,0087634288 | 64 |
| Симметрический косинус | 49 | 0,0061022025 | 48 |
6. Заключение
Активационная функция является одним из наиболее влиятельных параметров нейронной сети. Оценка результативности активационных функций показала, что разница между ними не слишком велика. Когда сеть обучена правильно, то каждая активационная функция дает приблизительно похожий результат. В статье четко показано насколько важна активационная функция. Выбор активационной функции для сети в целом или ее отдельного узла является важной задачей. Но, как показали результаты, если сеть с конкретной активационной функцией правильно обучена, то вероятность того, что другие активационные функции дадут такой же результат достаточно высока.
Мы подчеркиваем, что хотя выбор активационной функции для нейронной сети или ее узла является важной задачей, другие факторы, такие как обучающий алгоритм, размер сети и обучающие параметры, имеют более важное значение при обучении сети, так как результат работы на созданном тренажере показал, что при различных активационных функциях разница при обучении сети невелика.
Список использованной литературы
1. K. Homik, M. Stinchcombe and H. White. Multilayer feed forward networks are universal approximators, Neural Networks, vol. 2, pp.359–366, 1989.
2. C. Ji, R.R. Snapp and D. Psaltis. Generalizing smoothness constraints from discrete samples, Neural Computation, vol. 2, pp. 188–197, 1990.
3. T. Poggio and F. Girosi. Networks for approximation and learning. Proc. IEEE. vol. 78, no. 9, pp. 1481–1497. 1990.
4. Y. Le Cun. A theoretical framework for back propagation, in Proc.1988 Connectionist Models Summer School, D. Touretzky, G. Hinton and T. Sejnowski, Eds. June 17–26, 1988. San Mateo, CA: Morgan Kaufmann, pp. 21–28.
5. D.E. Rummelhart, G.E. Hinton and R.J. Williams. Parallel Distributed Processing: Explorations in the Microstructure of Cognition, vol. I. MIT Press, ch. 8.
6. James A. Freeman and David M. Skapura. Neural Networks Algorithms, Applications and Programming Techniques, pp.115–116, 1991.
7. Jacek M. Zurada. Introduction to Artificial Neural Systems, pp. 32–36, 2006.