Назад в библиотеку

УДК 519.71

О СРАВНЕНИИ ПОВЕДЕНИЯ ОДk–ЭТАЛОНА И АВТОМАТОВ, ПОРОЖДАЕМЫХ ЕГО ЛОКАЛЬНЫМИ ПРЕОБРАЗОВАНИЯМИ

Авторы:О.С. Швец, О.М. Копытова
Источник: Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС–2014) / Матерiали V мiжнародної науково–технiчної конференцiї студентiв, аспiрантiв та молодих вчених. Донецьк, ДонНТУ – 2014. – Т. 2 – С. 365–369.

Аннотация

Швец О.С., Копытова О.М. О сравнении поведения ОДk–эталона и автоматов, порождаемых его локальными преобразованиями. Рассматривается инициальный ОД–k автомат–эталон и класс автоматов, которые получаются из эталона переброской ровно одной дуги. Для указанного класса вводится бэровская метрика, позволяющая определить расстояние между любой парой автоматов. Найдена достижимая верхняя оценка для этого расстояния. Описаны подклассы автоматов, находящиеся на заданном расстоянии от эталона.

Ключевые слова:автомат, ОД–k автомат, поведение, переброска дуги, бэровская метрика.

Введение. Работа посвящена одной из классических и актуальных проблем теории конечных автоматов – задаче сравнения поведения автоматов с помощью экспериментов. Структура классов автоматов, близких по поведению в том или ином смысле, исследуется достаточно давно [1]. В основном эта задача рассматривалась в рамках теории экспериментов с автоматами [2]. Во многих случаях такие классы можно описать как результат последовательности специальных преобразований над дугами автомата–эталона. Преобразованием такого типа может быть, например, переброска дуг в графе переходов автомата, которую можно интерпретировать как «неисправность»  автомата в его схемной реализации.

Влияние перебросок на поведение автомата изучалось в [3–4], где основное внимание  было уделено выявлению условий, при которых исходный и преобразованный автоматы остаются изоморфными. В настоящей работе исследуется влияние одной переброски на поведение инициального определенно–диагностируемого порядка k эталона с точки зрения определения степени близости его поведения до и после переброски. Целью работы является:

1) поиск меры близости поведения эталона, являющегося инициальным ОД–k–автоматом,  и автомата, полученного из эталона переброской одной дуги, 

2) оценка этой меры близости;

3) описание класса автоматов с заданной степенью близости.

Постановка задачи. Неопределяемые понятия теории автоматов можно найти в [5].

Под автоматом будем понимать инициальный приведенный определенно–диагностируемый порядка k (ОД–k) автомат Мили A = ( S, X, Y, δ, λ, s0), где S, X, Y – конечные множества состояний, входных и выходных символов соответственно, δ, λ − функции переходов и выходов, а s0 – начальное состояние. При необходимости, чтобы не возникало путаницы, к обозначениям этих объектов будем добавлять индекс А или значок штриха.

Функции δ и λ обычным образом распространяются на множество  X*  всех входных слов конечной длины. Напомним, что автомат А называется ОД–k–автоматом, если k≥1 – наименьшее целое такое, что для любого входного слова p длины k и любой пары различных состояний  s∈S выполняется неравенство λ(s,p) ≠ λ′(t,p).

Будем говорить, что вход–выходное слово w=(p,q) порождается состоянием s автомата А, если λ(s,р)=q.  Длину слова w обозначим |w|. Два состояния s и t одного и того же автомата A или двух разных автоматов A и B соответственно, называются эквивалентными, если для всякого входного слова р∈X* выполняется λ(a,p)=λ′(b,p), где λ′ − функция выходов автомата A или B. Автомат называется приведенным, если все его состояния попарно неэквивалентны. Каждому состоянию s поставим в соответствие множество  λs  всех вход–выходных слов, порождаемых этим состоянием. Под поведением автомата А будем понимать множество λs0 вход–выходных слов, порождаемых его начальным состоянием.

Автомат удобно задавать в виде графа переходов, вершины которого соответствуют состояниям из S, а дугами являются четверки (s,x,y,t), где  t = δ(s,x),  y = λ(s,x). Пара (x,y) называется отметкой дуги, s –  ее началом, а  t – концом. Если e=(t,x,y,u) – дуга в графе переходов автомата A, то переброской этой дуги из состояния  u  в состояние v, отличное от u, называем замену её  дугой  (t,x,y,v). 

Пусть автомат A′  получен из автомата  A произвольной переброской одной дуги. Будем для определённости считать, что в результате переброски произошла замена дуги (t,x,y,u) на дугу (t,x,y,u), где  t,u,v∈S, u≠v. Состояния автомата A′ будем помечать штрихом так, что переброшенная дуга в нём имеет вид e′ = (t′, x, y, v′). Полученный автомат A′ назовём автоматом, локально порождённым из эталона А. Обозначим через K(A) класс всех автоматов, локально порождённых из  автомата А, включая сам эталон.  Интерес представляют следующие вопросы: 1) как определить степень близости поведения автоматов А и A′; 2) насколько изменилось поведение автомата после переброски дуги; 3) какова структура класса К(А) с точки зрения разбиения его на подклассы автоматов, эквивалентных по степени близости их поведения  поведению эталону.

Формализуем поставленную задачу. Введем на классе автоматов бэровскую метрику [6] следующим образом.  Пусть i – длина некоторого кратчайшего входного слова р, различающего начальные состояния s0 и s′0 автоматов  А  и  A′, т.е. слова, для которого λ(s0, р) ≠ λ′(s′0, р). Тогда положим:

 Ясно, что, чем длиннее различающее слово р, тем меньше расстояние между  А  и  A′. Пусть |X|=m и |S|=n. Каждая дуга заканчивается в одном из n состояний, и, следовательно, её можно перебросить в одно из оставшихся (n-1) состояний. Так как число дуг равно mn, то количество возможных перебросок равно mn(n-1), и, значит, класс К(А) состоит из (mn(n-1)+1) автоматов, включая эталон. Данный класс разбивается на подклассы Ki(A) автоматов, находящихся на одинаковом расстоянии 1/i от эталона. По определению, . Известно [6], что переброска одной дуги всегда приводит к неизоморфному автомату. Поэтому начальные состояния (s0, s′0) автоматов А и A′ всегда различимы некоторым словом, и, значит, . Заметим, что при переброске дуги её отметка не изменяется, т.е. состояния  s0 и s′0 выдают одну и ту же реакцию на каждый входной символ. Следовательно, длина различающего их слова больше или равна 2, откуда и К1(А)=∅. С другой стороны, пара состояний (s0,s′0) всегда различима некоторым входным словом длины, не превосходящей (2n-1), поэтому  Таким образом, . Итак, для класса К(А) существует разбиение на подклассы:

Задача состоит в следующем:

1)    для любой переброски дуги оценить ρ(A, A′);

2)    описать классы Ki(A) для i≥2.

Основные результаты.

Теорема 1. Пусть А – инициальный приведенный ОД–k–автомат и A′ получен из А переброской дуги (t,x,y,u) в состояние v. Тогда , где d – длина кратчайшего входного слова w такого, что  δ(s0,w)=t.

Доказательство. Чтобы отличать состояния автомата А от состояний A′, будем состояния последнего помечать штрихом и пару (s,s′) называть двойственными, где s∈S, s′∈S′. Покажем сначала, что состояния  u  и  v′  различимы некоторым словом длины, не большей k. Для этого воспользуемся приёмом, использованным при доказательстве того факта, что переброска дуги в любом приведенном автомате всегда приводит к автомату, не изоморфному исходному [7]. Построим автомат В, равный прямой сумме автоматов А и А′, и рассмотрим процесс построения Рk–таблиц [8] для автомата В.

Поскольку таблицы выходов автоматов А и А′ совпадают, то в таблице Р1 каждый класс эквивалентности  состоит из пар двойственных состояний. Заметим, что любая пара (s,s′), кроме пары (t,t′), по любому х опять переходит в пару двойственных состояний. Пара (t,t′) – единственная, для которой это не выполняется,  так как δB(t,x)=u и δB(t′,x)=v′. Отсюда следует, что пока состояния (t,t′) k–эквивалентны, любая пара (s,s′), отличная от (t,t′), будет (k+1)–эквивалентной. Сама же пара (t,t′) k–эквивалентна, пока пара (u,v′) является (k-1)–эквивалентной. Но, если (u,v′) (k-1)–эквивалентна, то тогда пары (t,t′), (u,u′), (v,v′) k–эквивалентны и, значит, состояния u,u′,v,v′ принадлежат одному классу эквивалентности в таблице Рk. Так как А ОД–k–автомат, то для некоторого i<k состояния u и v  будут (i-1)–эквивалентны, но i–различимы. И тогда i–различимыми будут и состояния u и  v′, где i≤k.

Пусть теперь w − кратчайшее входное слово в автомате А, переводящее его из начального состояния в состояние t, и р – кратчайшее слово, различающее  u  и v′. Пусть |w|=d,  |p|=i, и как показано выше, i≤k.  Ясно, что в автомате А′  δ(s′0,w)=t′. Тогда δ(s0, wx)=u, δ(s′0, wx)=v′, λ(s0, wx) = λ(s′0, wx), но λ(s0, wxp) ≠ λ(s′0,wxp), причём |wxp|≤d+1+k, что и требовалось доказать.

Покажем, что полученная оценка расстояния достижима.

Рассмотрим автономный автомат А на рис.1. Пусть  автомат А′  является результатом  переброски одной дуги в автомате А: дуга (1,0,0,2) перебрасывается в состояние 1 и заменяется дугой (1′,0,0,1′). Поскольку перебрасывается дуга, исходящая из начального состояния, то кратчайшее слово w имеет длину d=0. Легко видеть, что λ(s0,00)=λ(s′0,00), но λ(s0,000)≠ λ(s′0,000). Поэтому p=000 и |p|=3.  Отсюда . На примере видно, что в результате переброски дуги автомат A′ остался ОД2– автоматом.

Пример переброски одной дуги в автомате ОД2

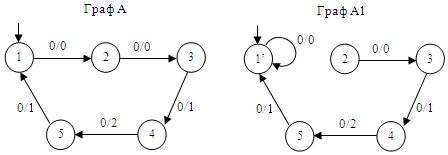
Рисунок 1 – Пример переброски одной дуги в автомате ОД2

Непосредственно из теоремы 1  вытекает следующее утверждение, в котором описывается структура класса К(А).

Пусть А′ есть результат переброски дуги (t,x,y,u) в состояние v и d – длина кратчайшего входного слова w, для которого  δ(s0,w)=t. Пусть также с – длина кратчайшего слова, различающего состояния u и v. Тогда справедлива следующая теорема.

Теорема 2. Класс Ki(A) состоит из всех тех автоматов А′, для которых выполняется следующее условие: d+с+1=i.

Выводы. В работе получены следующие результаты:

1)  найдена мера близости поведения пары автоматов, полученных друг из друга переброской одной дуги;

2)  найдена верхняя оценка указанной меры близости (теорема 1) и показано, что она достижима;

3)  описана структура классов автоматов, обладающих заданной степенью близости по поведению относительно эталона (теорема 2).

Данное описание структуры классов может быть положено в основу алгоритма их построения.

Литература

  1. Кудрявцев В.Б., Грунский И.С., Козловский В.А. Анализ поведения автоматов // Дискретная математика. – 2009. – 21, №1. – С. 3–35.
  2. Bhattacharyya A. Checking experiments on sequential machines. – New York: J. Wiley and Sons, 1989. – 155 с.
  3. Копытова О.М. Устойчивость автоматов к неисправностям их функции переходов // Труды ИПММ АН Украины. – 2010. – № 21. – С. 57–66.
  4. Копытова О.М. О структуре автоматов, сохраняющих поведение при перебросках дуг // Труды VIII Международной конференции "Дискретные модели в теории управляющих систем". – М.: Макс–Пресс, 2009, C. 155–159.
  5. Капитонова Ю.В., Кривий С.Л., Летичевский А.А., Луцкий Г.М., Печурин Н.К. Основы дискретной математики. – К.: Наукова думка, 2002. – 568 с.
  6. Кудявцев В.Б., Грунский И.С., Козловский В.А. Анализ и синтез абстрактных автоматов //Фундамент. и прикл. матем. – Т. 15, № 4. – 2009. – С. 101–175.
  7. Грунский И.С., Копытова О.М. О структуре контрольного эксперимента для определенно–диагностируемого автомата // Теория управляющих систем. – К.: Наук.думка, 1987. – С. 40–54.
  8. Гилл А. Введение в теорию конечных автоматов. – М.:Наука, 1966. – 272 с.