Українська   Русский
DonNTU   Masters' portal

Abstract

This work is in the development stage. More detailed and final information on this project will be provided after the completion of writing the thesis.

List

Introduction

Heat spreading in different environments makes a big influence on nature course of a lot of the important processes for practice. Therefore there’re a lot of mathematics and physics works dedicated to analysis questions associated with heat spreading.

Among of tasks connected with heat spreading we can emphasize an important class of tasks in which an examined substance undergoes changes and transgresses from one form to another with heat spreading or absorption as a result. Tasks like this (they called Stephan’s type tasks) appear in melting or consolidation of substance cases.

A particular property of that kind of tasks is a presence in moving surface division between those 2 stages (liquid and solid) at that, the rule of movement is unknown and it has to be determined. Exactly on that surface is going absorption or spreading of heat, which connected with stage transfer. Thermal properties of stages astride of driving surface can be different. Tasks of that class are obviously more difficult than tasks in which a transfer from one state to stage is absent.

An important and interesting task of this class is a process of crystalizing substance managing task.

Actuality of this work caused as a practical relevant of a fuzzy managing process of crystalizing for an object with a difficult geometry and a necessity in developing a strategy numerical solving of optimal managing of this process that makes holding at the theory of optimizing by difficult dynamic systems.

Practical tasks that spring up need a metal crystalizing process and an optimal managing of that process inasmuch it lets improve a quality of details and decrease costs at a separating detail from the form.

1. Problem definition

For determine optimal thermal-physics conditions of formation of bar were made calculations in the context of a mathematic model of thermal processes into a cylindrical bar [1], for the cored bar case (fig.1). In model that is used a liquid metal decants into crystallizer by portions, and a bar is drown out periodically. The bar’s surface is heated by three electronic beams inasmuch the capacity W3 of one from them is spread regularly in a central zone (R2 < r < R1), and another two W1 and W2 are concentrated in peripheral zones. At a mathematical model the W1, W2 and W3 are managed technological parameters that called beams capacities, poring periodicity τ, height of simultaneously pouring off to crystallizer portion h, deposition value of peripheral beam from the center toward stepped baffle of crystallizer d.

pic39

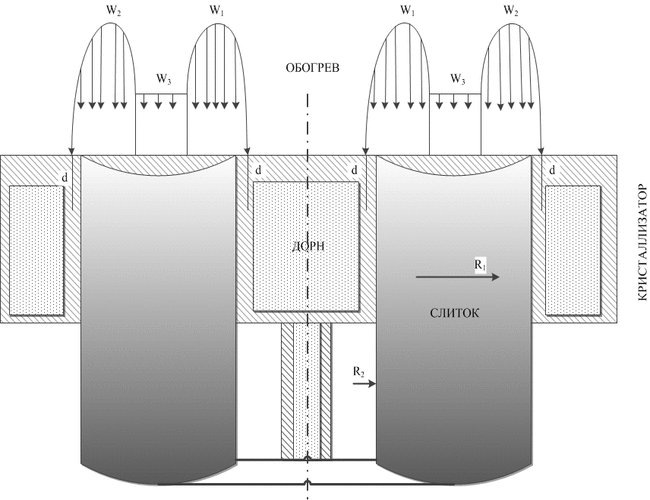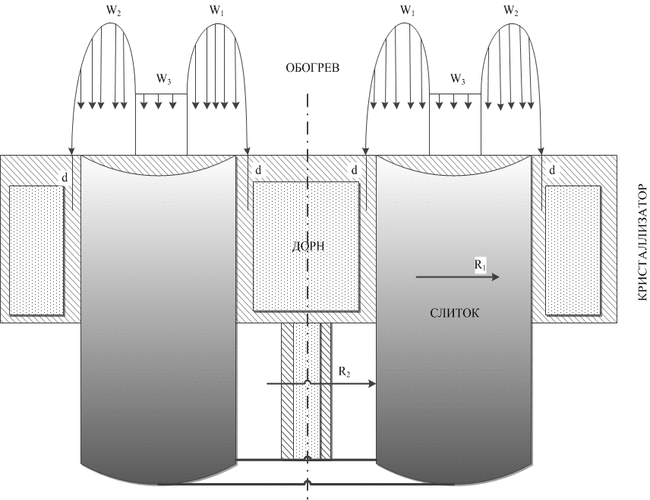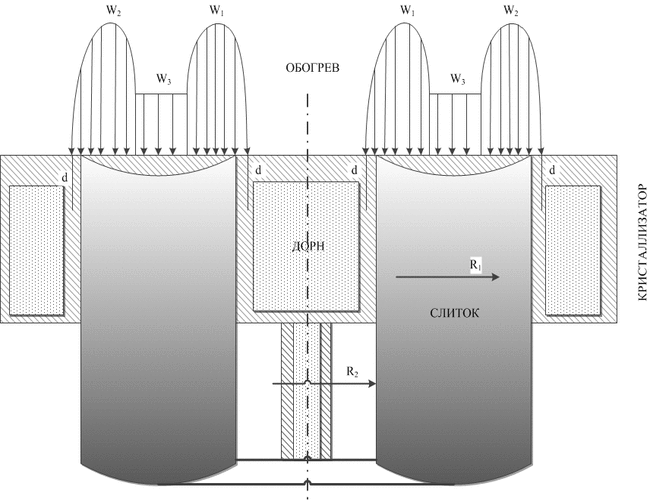
Figure 1 – The scheme of process of cored bar formation at ERMC ("обогрев" – "heating"; "дорн" – "mandrel"; "кристаллизатор" – "mold"; "слиток" – "bar")

A heat transferring process described by equation of thermal conductivity at the cylindrical frame of axes (r,O,z) for a case of axis symmetry. An axis OZ at frame of axes is equals to bar’s axis (axis of symmetry), and axis OR – with a radical direction. The start of coordinates is set on the bottom line of bar.

An thermal conductivity equal in this case is

pic40
R2 < r < R1; 0 < r < s(t); t > 0,

where c – specific heat; ρ – density; λ – coefficient of thermal conductivity; R1 and R2 – external and internal bar’s radiuses; s(t) – current height of bar.

Herewith boundary condition at the internal surface of bar is heat exchange with a wall of driftpin. According to relationship between the surface temperature of bar with a critical temperature TK (at which the surface of bar is separate from the wall of crystallizer), heat exchange between bar and crystallizer is realizing by different rules.

At T < TK – according to the rule of Stephan-Boltzman

pic41

ε – emissivity; σ – constant of Stephan-Boltzman; Tcρ – temperature of mold wall.

At T > TK – according to the rule of Newton-Richmann

pic52

α – coefficient heat exchange between a bar and a crystallizer.

2. Calculating of temperature field metods

We have got the next conditions:

U = X(x), Y(y)

pic42

X = C1cosλx + C2sinλx

pic43

(– λC1sinλx + C2cosλx) ± ω0(C1cosλx + C2sinλx) = 0

λtgx = ω0, λ = λn

Y″ + ωY′ – λ2Y = 0, Y = eμy

μ2 + ωμ – λ2 = 0

pic44

As a result we have n degree approximation in the general case in the presence of functionality minimizing

pic45

As an estimation of inaccuracy can be used:

pic46

3. Using fuzzy logic

This work researches a process of managing cooling of liquid substance in a foundry form that has a difficult structure. An objects cool is going in a special set that helps us to manage that process. Objects and sets of this type are used in a metallurgical industry.

Let the D = (–1 < x < 1, y < 0) a half-string that is full of solid metal. Let denote this as u(x,y) temperature of this metal. It needs to be determined a temperature u(x,y) with the next conditions:

uxx + uyy + ωuy = 0, (x,y) ∈ D,                   (1)
ux ± ω0u = 0, x = ±1,                                   (2)
u(x,–∞) = 0,                                                 (3)
uy(x,0) = ν(x), –1 ≤ x ≤ 1.                              (4)

ω and ω0 – are static Peclet and Nusselt’s numbers. A task solving (1–4) is

pic48

with a pic49, n = 1, 2, 3, …, λn – are positive squares of equation λ = ω0ctgλ.

Now identify a temperature u(x,y) with a temperature of a solid bar that disposed into crystallizer at the electronic refining. For the extracting of the bar from the crystallizer, the surface of the bar is heated by the three electronic beams W1, W2, W3, in which connection the capacity W3 of one of them regularly allocated in a central zone {–1 ≤ x ≤ 1, y = 0}, and two that left are concentrated by the parts x = ±1. Regardless of relationship between a surface of a bar whit a temperature T* in which connection the surface of the bar is separating from the walls of crystallizer nevertheless the heat exchange of the bar with the crystallizer is realized by the clause (2). For the finding a temperature of the bar is enough to put on in formula (5) ν(x) = (W1, W2, W3).

Than we inject a next functioanal

pic50

Flow ν(x) that needs to be determined from the admissible set U which supply a minimal value to functional I(ν). A minimizing sequence νn is built by the νn+1 = νn + εn(νn–1 – νn), clause, where an εn parameter is chosen from the min0≤εn≤1I(νn–1–νn)) clause. As a function U rage of definition is used a set of piecewise constant stepwise functions:

ν = νk, xk ≤ x ≤ xk+1, νk = const, k = 0, 1, 2, …, m

Herewith the (5) clause is:

pic51

and I(ν) = I(ν0,ν1, ν2, ..., νm).

At the numeric realization of the problem it has to be factored into a constraint 2500 ≤ ν(x) ≤ 5000,

where ν(x) – is a flow capacity as a unit of measure МW/m2.

Let the x1, x2, ..., xn – are factors that impacts on the process of crystallization and y1, y2, ..., yn – are conditions at which appears a new bar. Then a fuzzy managing in this type of problem is X(x1, x2, ..., xn)→Y(y1, y2, ..., yn).

For the sake of simplicity as a term-cloud of a linguistic variables x1, x2, x3, whereabout x1 = {"temperature"}, x2 = {"method of heating"}, x3 = {"ingot metal"}, we will use next clouds:

T = {"minimal","midrange","maximal"},

W = {"minimal","midrange","maximal"},

L = {"minimal","midrange","maximal"}.

Thereby we have x = (x1, x2, x3)→Y∈[α,β], whereabout α and β –are the numbers (the are chosen with a separating of a bar from the walls of crystallizer) and for the outlet linguistic variable Y (a temperature of the bar surface) will be used a term-cloud Q = {"minimal","midrange","maximal"}.

A numerical calculation that helps us to build a fuzzy managing is realizing with a help of Mamdany’s algorithm. Whreabout was used the next parameters value: 400мм ≤ L ≤ 6000мм, 2500 Вт/м2 ≤ W ≤ 5000 Вт/м2.

References

  1. Жук Г.В., Ахонина Л.В., Тригуб Н.П. Математическое моделирование процессов кристаллизации титанового сплава Ti–6A1–4V при ЭЛПЕ // Там же. – 1998. – № 2 – С. 21–25.
  2. Миненко А.С., Шевченко А.И. Приближенный анализ пространственной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 10 – С. 29–33.
  3. Миненко А.С., Шевченко А.И. Приближенный анализ стационарной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 5 – С. 36–40.
  4. Миненко А.С., Шевченко А.И. Приближенный анализ многомерной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 4 – С. 30–34.
  5. Миненко А.С. Математическое моделирование процессов кристаллизации металла // Искусственный интеллект. – 2010. – № 2 – С. 37–43.
  6. Миненко А.С., Исследование стационарной конвективной математической модели кристаллизации вещества // Искусственный интеллект. – 2010. – № 1 – С. 103–107.
  7. Шевченко А.И., Миненко А.С. Математическое моделирование процессов кристаллизации металла с учетом конвекции и примесей // Доповіді НАН України. – 2011. – № 6 – С. 35–39.
  8. Миненко А.С., Шевченко А.И. Задача Стефана при наличии конвекции // Доповіді НАН України. – 2012. – № 1 – С. 35–39.
  9. Миненко А.С., Гунько С.А. Численный анализ конвективной модели кристаллизации // Искусственный интеллект. – 2012. – № 1 – С. 43–48.
  10. Миненко А.С. Приближенный анализ нелинейной конвективной математической модели // Искусственный интеллект. – 2012. – № 1 – С. 36–43.
  11. Миненко А.С., Павлыш В.Н. Применение математического моделирования в задачах управления информационными процессами с элементами нечеткой логики при автоматизации технических систем. // Збірник наукових праць Донецького державного університету управління. Серія: Державне управління. Випуск: Соціальний менеджмнет і управління інформаційними процесами – Донецьк: ДонДУУ, 2010. – С. 43–48.
  12. Миненко А.С., Волченко Е.В., Шишкин С.А. Метод построения взвешенных временных рядов для решения задачи прогнозирования // Східно-Європейський журнал передових технологій. – Харків, 2012. – № 2(56). – С. 20–34.
  13. Миненко А.С., Шевченко А.И. Методы исследования нелинейных математических моделей. – Київ: Наукова думка, 2012. – 130 с.
  14. Шевченко А.И., Миненко А.С., Золотухина О.А. Численный анализ одной нелинейной математической модели // Доповіді НАН України. – 2012. – № 10 – С. 35–38.
  15. Миненко А.С., Шевченко А.И. Методы исследования нелинейных математических моделей – Національна академія наук України Інститут проблем штучного інтелекту, Донецьк, 2012. – 132 с..
  16. Шевченко А.И., Миненко А.С. Математическое моделирование одного класса сложных систем с применением нечеткой логики // Доповіді НАН України. – 2013. – № 5 – С. 51–54.
  17. Шевченко А.И., Миненко А.С. Моделирование потенциально-вихревого течения со свободной границей с применением нечеткой логики // Доповіді НАН України. – 2013. – № 6 – С. 47–51.
  18. Шевченко А.И., Миненко А.С., Сыпко И.А. Моделирование одного класса сложных систем с нечетким управлением // Доповіді НАН України. – 2013. – № 8 – С. 52–54.
  19. Шевченко А.И., Миненко А.С. Об одном классе интегральных функционалов с неизвестной областью интегрирования // Доповіді НАН України. – 2013. – № 12 – С. 48–52.
  20. Миненко А.С., Шевченко А.И., Сыпко И.А., Гололобова А.С. Нечеткое управление в нелинейных теплофизических моделях. // Праці міжнародної конференції Питання оптимізації обчислень (ПОО-XL), К.: Інститут кібернетики ім. В.М. Глушкова, 2013. – С. 275–277.