Математическое моделирование динамических процессов в одноконцевой подъемной машине в канатами большой длины
Автор: Сребная Е. Г., Кондрахин В. П.
Источник: Подъемно-транспортное оборудование и логистика: V региональная студенческая конференция. г. Донецк, 20-21 мая 2015 г. – Донецк: ДонНТУ, 2015.
Аннотация
Сребная Е. Г., Кондрахин В. П. Математическое моделирование динамических процессов в одноконцевой подъемной машине в канатами большой длины Выведены уравнения динамического процесса для одноконцевой подъемной машины с учетом того, что канат разделен на некоторое количество распределенных масс, связанных упруго-диссипативными элементами.
Содержание работы
Добыча природного минерального сырья создает материальную базу промышленного производства, удовлетворяя потребности общества в металлах, топливе, строительных и химических материалах. Значительная часть полезных ископаемых добывается на предприятиях с подземными горными работами, что предполагает широкое применение шахтных подъемных установок для транспортировки горной массы на поверхность. .
Подъемные установки являются одним из основных элементов транспорта на горных предприятиях. Надежность и высокая производительность шахтного подъема во многом определяет эффективную работу предприятия в целом.
Большие массы шахтной машины, движущиеся с большими скоростями, вызывают сложные динамические процессы при пусках и торможениях. Динамические процессы формируют чрезмерные нагрузки, прогрессирующие усталостные явления отдельных элементов конструкции, которые приводят к аварийным ситуациям и катастрофам.
Теоретическим фундаментом динамических расчетов является теория механических колебаний. Знания законов колебательных процессов позволяют спроектировать рациональные конструкции машин.
Это делает задачу определения динамических усилий в канате актуальной с практической и научной точки зрения.
Научную основу данной работы составляют исследования вопроса о динамических нагрузках в подъемых машинах таких выдающихся ученых, как В. И. Дворников и А. Г. Степанов.
Подъемный канат представлен профессором Дворниковым В. И. в виде упругой невесомой нити [1, 2]. Масса каната приведена к сосредоточенной массе сосуда. Справедливость данного допущения зависит от длины уравновешивающего каната. При малой длине уравновешивающего каната его распределенная масса оказывает несущественное влияние на динамические процессы. Выполненные исследования для существующих неуравновешенных подъемных установок, при принятых допущениях, дают значение частотных и амплитудных величин, которые сравнимы с решением этой задачи в частных производных. Принятие этого допущения существенно уменьшает трудоемкость решения. Однако при больших длинах каната появляются большие погрешности в определении динамических усилий в канатах. Для того, чтобы избежать больших погрешностей, распределенную массу этого каната рекомендуется разбить на несколько равных масс, соединенных невесомыми вязкоупругими связями.
Динамикой подъемных машин с подобным учетом массы упругих элементов занимался доктор технических наук, профессор Степанов А. Г. [3, 4, 5]. В своих работах он предлагает эквивалентную схему, в которой головные и уравновешивающие канаты разбиты на некоторое количество частей, представляющих собой массы, соединенные вязкоупругими связями. Однако в рассматриваемых работах отсутствуют рекомендации по выбору количества масс, на которые следует разбивать канат заданной длины.
Учитывая теоретические исследования выше приведенных авторов, автор данной работы предлагает заменить канат большой длины некоторым количеством распределенных упругих диссипативных масс, а в дальнейшем уточнить их число.
Целью данной работы является математическое моделирование динамических процессов одноконцевой подъемной машины с канатом большой длины.
Для достижения вышеуказанной цели поставлены следующие задачи:
- Разработать расчетную динамическую схему одноконцевой подъемной машины с учетом замены каната некоторым количеством масс и упруго-диссипативных элементов.
- Вывести выражения для функции Лагранжа заданной схемы одноконцевой машины.
- Вывести уравнения движения путем вычисления производных от функций кинетической, потенциальной энергии и диссипативной функции Рэлея.
Для решения поставленных задач используется подъемная одноконцевая машина (рис. 1), которая состоит из барабана машины с приведенными к нему моментами инерции вращающихся частей редуктора и ротора электродвигателя с кинетическим моментом инерции Jб, направляющего шкива с моментом инерции Jш, наклонной струны каната lcтр, считающейся неизменяющейся во времени, и отвесной части каната lотв, на которой закреплена масса концевого груза mn.
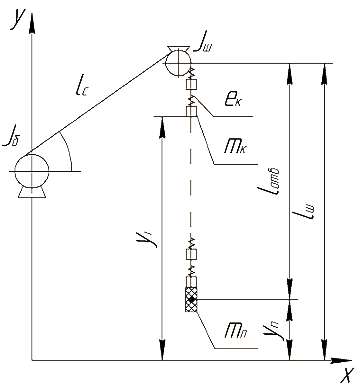
Рисунок 1 – Расчетная схема одноконцевой подъемной машины
Отвесный канат подъемной машины разбит на некоторое количество распределенных масс mk с координатами yi, связанных между собой упругими связями ek. Концевой груз mn имеет перемещение yn по вертикали, отсчитываемое от некоторого исходного положения груза.
При выводе уравнений движения приняты следующие допущения:
- Считаем функции, зависимые от времени, медленно изменяющимися. Концепция медленно изменяющихся функций позволяет рассматривать систему как адиабатическую, то есть как систему с якобы постоянными коэффициентами, а затем в полученных решениях уже учесть их фактическую «медленную» зависимость от времени. Вследствии этого примем, что коэффициент податливости первого элемента е1 остается неизменной.
- Так как моделирование будет проходить в течении сравнительно небольшого участка времени, то можно принять, что за это время количество масс каната не поменяется.
Для вывода уравнений динамики машины используем уравнения Лагранжа ІІ рода:
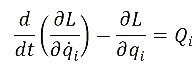 .
.
Так как сила сопротивления участков каната пропорциональна скорости движения, то на каждый участок дополнительно будут действовать диссипативные силы. С учетом функции Рэлея уравнения Лагранжа ІІ рода примут вид:
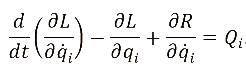 .
.
Кинетическая энергия такой системы будет состоять из суммы кинетических энергий трех рассматриваемых сосредоточенных масс, струны и отвеса и примет вид:
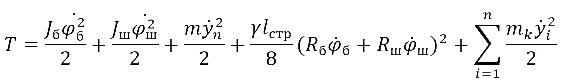 .
.
Потенциальная энергия будет состоять из потенциальной энергии сил упругой деформации струны и отвеса при принятых допущениях и гравитационной части с учетом, что струна наклонена к горизонту под углом:
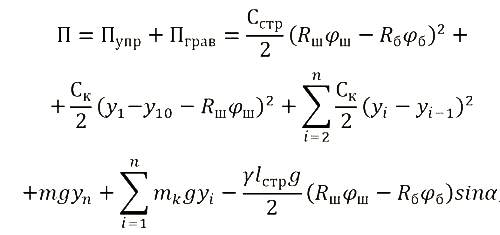 .
.
где: Сстр – коэффициент жесткости струны, Ск – коэффициент жесткости i–ой части отвеса, y1 – положение первой упруго–диссипативной массы отвеса, y10 – начальное положение первой массы.
Функция Лагранжа представляет собой разность кинетической и потенциальной энергий системы и для данного случая будет иметь вид:
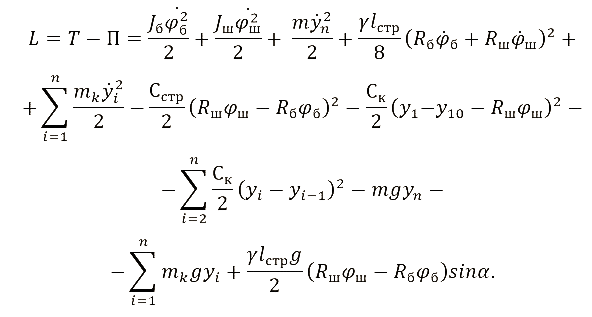 .
.
Определим в качестве обобщенных координат элементов рассматриваемой системы переменные
тогда соответственно в качестве обобщенных скоростей
Обобщенные непотенциальные силы Q1, Q2, Qi (i=1...n) для рассматриваемой системы примем следующими: Q1=Mдв(t), Q2=0, Qi=0 (i=1...n), где Mдв(t) – приведенный к оси барабана момент, развиваемый двигателем, и эту переменную будем считать известной функцией от времени.
Обобщенные силы Q2, Qi (i=1...n) приняты равными нулю, так как предполагается, что шкив и концевой груз не подвержены действию иных внешних сил, кроме уже учтенных.
Произведя необходимые вычисления производных от функции Лагранжа, в итоге получим искомые уравнения движения:
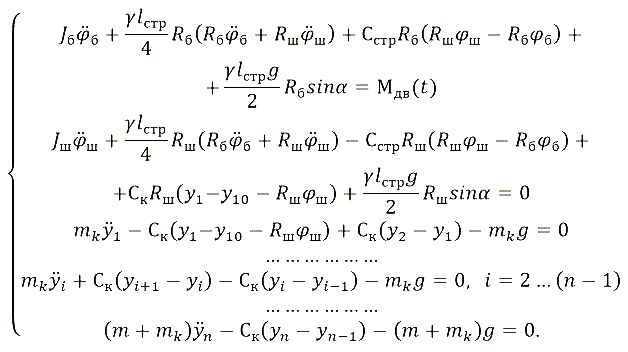 .
.
Поскольку упругие и диссипативные элементы связей располагаются параллельно, то при учете диссипативных сил, не записывая выражение для функции Рэлея, легко получить итоговую математическую модель рассматриваемой динамической системы путем добавления диссипативных составляющих:
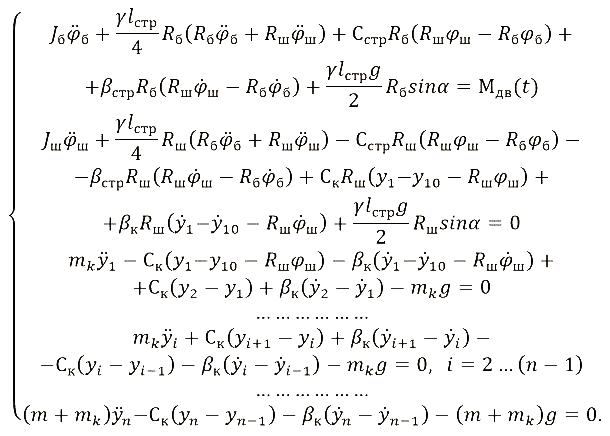 .
.
Вывод
Полученные уравнения движения (5) позволяют определить динамические нагрузки, действующие на барабан, шкив, груз, а также на каждый отрезок каната во время пуска машины, ее работы и торможения. Разработанную математическую можно применять для любых одноконцевых подъемных машин.
Список использованной литературы
- Дворников В. И. Теоретические основы динамики шахтного подъемного комплекса / В. И. Дворников, Е. Р. Къерцелин. – София, МОНТ, 1997. – 363 с.
- Дворников В. И., Къерцелин Е. Р., Трибухин В. А., Савенко Э. С. Динамические жесткости канатов шахтных подъемных установок / Дворников В. И., Къерцелин Е. Р., Трибухин В. А., Савенко Э. С. // Стальные канаты. – Одесса, 2003.
- Степанов А. Г. Динамика шахтных подъёмных установок / А. Г. Степанов. – Пермь : УрО РАН, 1994. – 263 с.
- Степанов А. Г., Корняков М. В. Динамика машин : монография. – 2–е изд., испр. и доп. / Степанов А. Г., Корняков М. В. – Иркутск : Изд–во ИрГТУ, 2014. – 412 с.
- Степанов А. Г. Динамические процессы при скольжении канатов по футеровке барабана многоканатной подъемной установки / Степанов А. Г. // Горное оборудование и электромеханика. № 6. 2010. – С. 24–35.