Modelling of vibrations of hoisting systems
Автор: Tejszerska D., Switonski E.
Источник: Европейский конгресс по вычислительным методам в прикладных науках и инженерии. ECCOMAS 2000. Барселона, 11-14 сентября 2000 г.
Аннотация
Tejszerska D., Switonski E. Modelling of vibrations of hoisting systems Разработана компьютерная программа моделирования колебаний подъемных систем при дополнительных конструктивных и технологических параметрах.
Abstract
Serious dynamic interactions occur in elements of hoisting systems, during normal operation and in emergency states. Longitudinal vibrations, mainly dependent on processes of starting and braking, cause fatigue wear of ropes, being one of main reasons of their replacement. The vibrations increase the intensity of sliding of single ropes, eroding lining of pulleys. Transverse vibrations, depending on the design of cage and condition of shaft guides, cause forces, resulting in erosion of guides and fatigue wear of cage elements. Dynamic effects in emergency states can cause failure of the whole hoisting system.
The present state of knowledge of dynamics of hoisting systems and available modern computer hardware enable to formulate and solve complex models, well representing processes occurring in a real system and allowing qualitative and quantitative evaluation, but among many published works, analysing particular phenomena in hoisting systems, it was not found the model, simulating jointly the whole process of coupled transverse and longitudinal vibrations.
The model of coupled transverse and longitudinal vibrations of hoisting system, caused by determined course of winding machine driving moment or acceleration, and by stochastic distribution of irregularities of shaft guides is presented in this work. Multirope system, with flexible cages, equipped with rollers and slide shoes, interacting with flexible shaft guides is analysed. Impact of dynamically varying forces in ropes – on the transverse vibrations, and of the friction forces, resulting from rollers interactions, on the longitudinal vibrations is considered. The phenomena connected with variations of load, carried by each rope, sliding of ropes and movement of suspension elements are included. The effects of variations of length of branches and stiffness of individual ropes, friction and internal damping as well as the possibility of system asymmetry were taken into account. Complex form of interaction between rollers and guides, including existence of clearances or preliminary thrust, mating of rollers and slide shoes and various stiffness of shaft guides in different points were considered.
Non–linear system of partial and ordinary differential equations, which defines the behaviour of the model, was solved numerically. Ropes were divided on finite elements and time derivatives were replaced by finite differences, giving the system of ordinary linear equations, with parameters changed in every time step The results of simulation were compared with published experimental data, measured in the same hoisting system, and good agreement was obtained.
Exemplary results of simulation demonstrate the possibilities of developed model and computer program. Extensive investigation of influence of parameters of the system on its vibrations is actually performed with the use of model and program. It will facilitate the selection of optimal parameters of designed hoisting systems as well as improvement of existing systems operation.
1. Introduction
Vibrations of non-linear discrete-continuous systems occur very frequently in engineering practice and in scientific considerations. Nevertheless, they still need further studies, improving mathematical description of the process and the methods of numerical simulation. The modelling of vibrations of mine hoisting system is a typical example of such problem.
Published studies include, among others, analyses of emergency braking, conditions of sliding, reasons of changes of load, carried by each rope, investigations of frequency characteristics of elastic cage and computer simulation of transverse vibrations of stiff cage [1,3,7]. Simple, three mass models of the system are still performed [2] . The model of hoisting process, jointly describing the set of phenomena, listed on next page, which consideration is characteristic for presented work – wasn't yet found in the literature.
2. Modelled hoisting system
The moving system, consisting of longitudinally vibrating lifting and balance ropes, longitudinally and transversely vibrating cages and torsionally vibrating pulleys, with consideration of different forms of contact between ropes, pulley, cage and guides – is the subject of this study. The scheme of analysed hoisting system is presented on fig. 1.
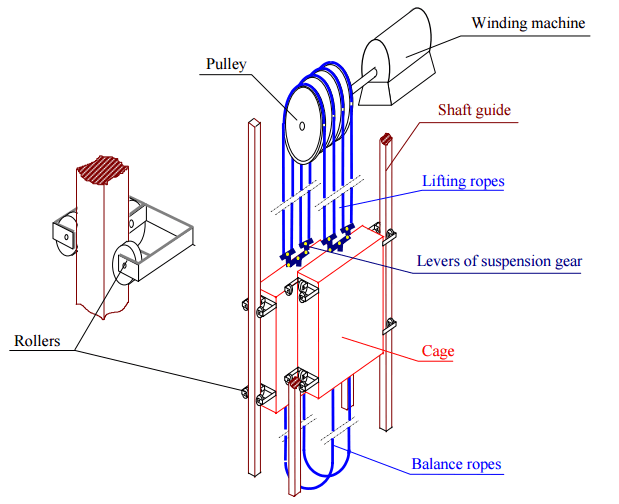
Fig. 1. Scheme of analysed hoisting system
Longitudinal vibrations, dependent mainly on processes of starting and braking, cause fatigue wear of ropes, which, apart from corrosion, is a main reason of their replacement. The vibrations increase the intensity of sliding of single ropes, which erode pulleys lining Great vibrations in emergency states may cause failure of all hoisting system.
Transverse vibrations of cages, excited by irregularities of guides, cause great dynamic stresses in cage beams and interactions between cage and guides, resulting in erosion of guides and fatigue wear of cage elements.
The phenomena listed below are analysed, formulating the model of system vibrations:
- Vibrations of discrete one-dimensional finite elements on which are divided modelled ropes, with consideration of their inertia, elasticity and damping characteristics.
- Movement of pulley and elements of rope, passing around it, with analyses of frictional coupling and changes of boundary conditions, resulting from contact of both objects.
- Longitudinal movement of the cage, connected by moving suspension gear with elastic elements of vibrating rope.
- Transverse movement of the deformable cage, with consideration of different forms of its contact with guides.
Formulated mathematical model of vibrations [6] takes into account:
- Variations of length of both branches of ropes.
- Dependence between stresses in ropes and their stiffness and unscrewing moment.
- Existence of clearance or preliminary thrust between roller or shoe and guide.
- Co-operation of rollers and slide shoes.
- One-sided or double–sided action of rollers.
- Elasticity of cage, treated as a system consisting of three parts: rigid upper head and bottom frame, connected by the group of elastic bent beams, reinforced by transverse rods or stiff plates of cage floors.
- Periodic changes of elasticity of guide in the point of its contact with cage, resulting from properties of multispan beam, elastically supported.
- Aerodynamical drag, friction and internal viscous damping in rollers and ropes.
- Influence of forces and unscrewing moments in ropes on cage.
- Diversification of parameters of individual ropes, and diameters of rope grooves in pulley in multirope system, causing variations of loads, carried by every rope.
- Asymmetry of cage structure and load,
Longitudinal vibrations are excited mainly by the process of starting or braking. Smaller vibrations are caused by loading the skip. Kinematic and dynamic excitations are analysed in the form of given transients of acceleration of pulley or driving moment of winding machine. Different forms of irregularities of guides are treated as a main cause of transverse vibrations.
Transverse vibrations are excited also by coupling with longitudinal vibrations – through variations of tensions in ropes, and their moments, turning the cage. Changes of frictional forces, caused by transverse vibrations, additionally excite longitudinal vibrations.
3. Mathematical model of longitudinal vibrations
Longitudinal vibrations of massive (ρ) elastic (EA) rope, with consideration of viscous damping (ν) are described by partial differential equations. Every rope was divided on discrete one–dimensional finite elements. Relations describing dependence of forces in ropes on mutual displacements of neighbouring elements were defined. Ordinary differential equations of dynamic equilibrium. describing movement of elements were formulated.
Separate, more complex form of equations was obtained for special discrete elements of rope – placed in the vicinity of the pulley, cages or bottom loop of balance rope.
The difference of forces in rope on both sides of pulley is the reason of phenomenon of sliding. Difference of strains, depending on forces, causes the shortening or elongation of every element of rope before leaving the pulley and its shifting along the part or all perimeter. The sliding occurs when the ratio of forces in ropes on both sides of pulley achieves the value determined by equation of Euler–Eytelwein: Increase of the ratio of forces stops then, and the influence of factors tending to its enlargement is compensated by sliding. The relationship determining the sliding displacement of rope in respect to the pulley as a function of necessary equalising changes of forces in both branches of rope was formulated.. The value of sliding displacement was introduced into terms describing forces in ropes in equations of dynamic equilibrium of pulley and discrete elements of rope, situated in its vicinity.
Similar method was used for modelling movement of levers of suspension gears. When the moments, resulting from differences of forces in individual ropes are greater than moments of friction in bearing – the levers move, causing additive displacements of ends of ropes and changes of forces
Modulus of elasticity of ropes (E) reveals experimentally ascertained parabolic dependence on stresses in ropes. This property was introduced in the model, by changing adequate coefficients of equations in every time step, basing on values of forces calculated in last step.
In closed kinematic chain, formed by hoisting system – the role of links, connecting the lifting and balance ropes if fulfilled by the cages. Elongations of cages are much lower, than strains of ropes – so, for analysis of longitudinal vibrations - cages may be treated as massive particles. The equation of dynamic equilibrium of cage in vertical direction includes massive and inertial forces, the forces in connected ropes and the drag force. The drag was divided onto three components, describing viscous friction (proportional to the velocity of cage), sliding friction (not dependent on velocity), and aerodynamic drag (proportional to square of velocity). Two first components are proportional to the sum of forces acting between rollers and cage, and constitute coupling between transverse and longitudinal vibrations.
4. Mathematical model of transverse vibrations
The cage in a model of transverse vibrations is frequently treated as a rigid body, supported by elastic rollers [7] . However, the bending stiffness of cage is much lower than longitudinal. More precise modelling of strains of cage and specially of mutual displacements of supports of rollers on cage heads is very important for proper calculation of interactions between cage and guides. For this purpose the model of deformable cage was formulated in this work.
The cage is treated as a system of two rigid frames, connected by four main and some auxiliary elastic longitudinal beams. The transverse bending deformations of these beams are much greater than elongation. It is therefore assumed that changes of distance of heads may be neglected. Mutual displacement of heads is treated as a plane motion. The longitudinal beams are reinforced by transverse rods or stiff plates of cage floors. The bending stiffness of side metal sheets is approximately added to longitudinal beams. Full symmetry of the cage structure is assumed for stiffness calculation.
Performed analysis of equation of bending axis of longitudinal beam, with simplified assumption of uniformity of transverse inertial load – showed, that the displacements of upper and lower ends of beam, measured from its geometric centre, have nearly equal values (and opposite directions).
Simplified calculation of coefficients, describing dependence between forces, acting on heads and ends of beams, maximal stresses in beams and mutual displacements of heads, was introduced in model [5] . Bending of cage in two perpendicular directions was analysed independently.
Dynamic equilibrium of the cage, hanged on lifting ropes, burdened by load and by balance ropes, and interacting with shaft guides through rollers and slide shoes, is analysed. The changes of forces and unscrewing moments in ropes, caused by longitudinal vibrations, constitute coupling between longitudinal and transverse vibrations.
The transverse vibrations of the cage are described by eight co–ordinates. Five of them refers to the central part of cage – two displacements of its mass centre(ys, zs) and three angles of rotation (φ,ψ,η). The mutual movement of heads is described by three additive co-ordinates – two displacements (Δys, Δzs) and one angle of rotation (Δφ)
The following dynamic forces, acting on the whole cage, and separately on the upper head, are considered, accordingly to assumptions listed in par. 2): forces and moments of inertia, tensions in ropes, unscrewing moments in ropes, forces acting on guides, together with frictional forces, and forces, acting between heads and body of the cage, resulting from the stiffness and distortion of cage.
The possible asymmetry of guides or suspension gear, and shift of the mass centre of the cage in respect to its geometric centre, resulting from structural asymmetry and unbalancing of load – are introduced. Optional number of one–sided or double–sided rollers, acting in two horizontal directions, placed in the defined distance from the mass centre is provided. The number of considered lifting and balance ropes is also optional in the model.
Cage contacts with guides through rollers, with one-sided or double–sided action, having defined stiffness, damping properties and nominal clearance or preliminary thrust.. In moments of greater transverse displacements – the protective slide shoe, having much greater stiffness and additive nominal clearance – contacts with the guide. Stiffness of guide and its irregularity (deviation from theoretical straight line, and possible local unevenness) in the point of contact with roller are also considered.
Consideration of guide elasticity is important in systems having stiff rollers. Guide is treated as multispan elastic beam, supported by transverse elastic girder. The chosen number of analysed spans is enough to enable neglecting of influence of null border conditions on its end and not too great to avoid bad conditioning of obtained equations. Two positions of force – in the middle of span and upon the girder – are considered. Values for other positions are harmonically interpolated. The equation of bending axis is solved numerically (for the symmetric half of analysed part of guide) and the stiffness is calculated as the ratio of force to deflection.
Final relationship, describing dependence of force acting between cage and guide, on mutual position of cage and guide has different form for different stages of contact – from clearance or thrust position to stroke of slide shoe.
5. Method of solving model equations
The mathematical model, describing vibrations of assumed physical model of mine hoist, has the form of non–linear system of partial and ordinary differential equations. After division of continuous ropes onto discrete the mathematical model assumes a form of system of non-linear ordinary differential equations, binding accelerations, velocities and displacements of pulley (u), two cages, uplifting and falling (u,f – ys,u, zs,u,...Δ φf) and all discrete elements (i, j) of lifting and balance ropes (k,l – ...xi,k,...xj,l...):
The system is solved numerically by substitution of time derivatives by adequate finite difference expressions [5], based on parabolic splines of time transients of all considered dynamic displacements in every time step Δt.
Accelerations and average values of displacements and velocities in the time step Δt, introduced into equations of dynamic equilibrium, are expressed by values on the borders of time step. Method of parabolic splines was chosen as the most convenient for the purposes of the work, after analysis of the simplicity of programming, precision, time of calculation and stability of some methods of integration of ordinary differential equations [5].
Three sets of linear algebraic equations, with coefficients varying in time are obtained as a result of discretization. They define dependence of all considered displacements in the end of time step on displacements and velocities in the beginning of step, for longitudinal vibrations of system and for transverse vibration of two cages :

These equations are solved by triangular reduction, with selection of main element and full utilisation of properties of sparse main matrix A of a set, describing longitudinal vibrations. All three sets are solved parallelly, with introduction of forces in ropes, calculated by the model of longitudinal vibrations, and frictional forces, calculated by transverse vibrations model - into equations of dynamic equilibrium of cage in the model of other vibrations.
The values of forces in ropes and acting on guides, stresses in ropes and in main supporting beams of cages, accelerations and velocities of all elements, in the end of time step, are then calculated. The values of displacements x'... and velocities x'... in the end of time step are treated as starting values for the next time step. Elements of main matrices C, describing different forms of contact between rollers and guides, and elements of matrix A connected with variations of elasticity modulus of rope, caused by changes of stresses, with sliding of individual ropes on pulley and with motion of suspension gear – are corrected in every time step, together with calculation of elements of column matrices B, D, containing values of displacements and velocities in the beginning of time step and actual values of excitations and other parameters.
Every change in condition of contact of one of rollers or shoes with guide – strongly changes its effective stiffness and coefficients of matrices C,D. After determination of displacements in the end of time step the conditions of contact of every roller are checked. If they are different from initial – then the first time instant of their change (inside time step Δt) is calculated, basing on above mentioned parabolic approximation of transient of every displacement. Interpolated values for this time instant are treated as initial for next time step
The stationary positions of cages and tensions in ropes are calculated before starting the simulation of vibrations. These calculations are necessary – their lack should introduce the disturbance in the first period of motion, having the form of really non existing dynamic excitation. The equations describing stationary state are slightly simpler, but similar to general dynamic equations [5]. Calculations of initial stationary state are performed iteratively.
Kinematic and dynamic excitations of longitudinal vibrations are analysed. Different forms of acceleration of winding machine, from step through trapezoid and irregular polygon to simple controller, adjusting moments of winding machine to desired form of velocity profile are considered.
Irregularities of shaft guides, being main excitation of transverse vibrations, include deviations from straight vertical line of their joints with girders and local unevennesses of connections of individual guide beams, small but very step. Their values are calculated by random generator, accordingly to assumed stochastic characteristics.
The lengths of time steps are calculated, basing on periods of natural vibrations of simple models. For longitudinal vibrations three body system is analysed, consisting of massive pulley and two cages, connected by elastic ropes, with masses included into considered bodies. For transverse vibrations – the stiff cage is considered, supported by the average number of elastic rollers, contacting with guide. The time step is shortened when roller passes along local unevenness.
Formulated mathematical model produced the basis for elaboration of computer program, simulating coupled longitudinal and transverse vibrations of multirope hoisting system. Program consists of segments, serving for calculation, preparation of input data and graphical presentation of results. It's written in Turbopascal.
The model was verified by comparison of ranges of stresses, forces and accelerations, obtained by computer simulation, with published experimental data. Precise experimental values, including not only graphs of acceleration of cage, but also all design parameters of the system and graphs of acceleration of the winding machine (being kinematic excitation of vibrations) – were used for verification of the model of longitudinal vibrations. Very good agreement was obtained with results of simulation of the same system, excited by the same form of acceleration of winding machine.
6. Exemplary results of computer simulation
The set of numeric experiments was performed with the use of program. Some examples of obtained graphs, showing possibilities of the program and sensitivity of the model to variations of important parameters, are presented on following pages.
First group of graphs. presents dependence between dynamic forces in ropes or moments acting on pulley – and the form of winding machine acceleration. It shows great decrease of vibrations when the form of excitation changes from stepwise to trapezoid, and possibility of optimisation of winding machine control (fig. 2).
Second group presents example of dependence between forces in side rollers, with double sided action and stresses in main supporting beams of cage – and values of roller stiffness, showing great influence of this parameter and possibility of optimisation. (fig. 3).
Third group shows similar dependence between forces in frontal, one-sided rollers and stresses in main supporting beams of cage – and preliminary thrust or clearance between nominal position of roller and guide, also showing possibility of optimisation (fig. 4).
Last graph shows great variations of load carried by individual ropes during the motion of cage from lower to higher level, caused by differences of diameters of rope grooves in winding machine lining, different preliminary stresses, Young modulus and by movement of elements of suspension gear (fig. 5).
7. Conclusions
Elaborated model and computer program enable simulation of vibrations of hoisting systems, having optional design and process parameters. It will facilitate the selection of optimal parameters of designed hoisting systems as well as improvement of existing systems operation. Extensive investigation of influence of parameters of the system on its vibrations is actually performed with the use of model and program.
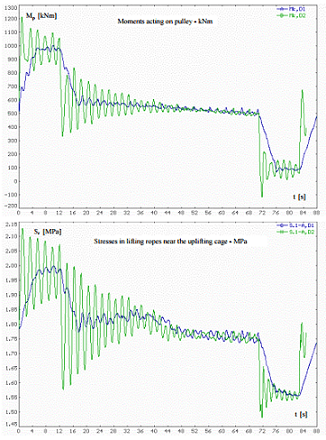
Fig. 2. Influence of form of changes of acceleration of winding machine from stepwise (D2) to trapezoid (D1) on dynamic forces in ropes and moments acting on pulley
![Stresses in supporting beams in cage [MPa] Stresses in supporting beams in cage [MPa]](images/7pic5.png)
Fig. 3.a – Stresses in supporting beams in cage [MPa]
![Forces between rollers and guides [kN] Forces between rollers and guides [kN]](images/7pic6.png)
Fig. 3.b – Forces between rollers and guides [kN]
Fig. 3. Influence of stiffness of rollers (D1..D3 - 5,2,10 kN/cm):on stresses in cage and forces in rollers
![Stresses in supporting beams in cage [MPa] Stresses in supporting beams in cage [MPa]](images/7pic7.png)
Fig. 4.a – Stresses in supporting beams in cage [MPa]
![Forces between rollers and guides [kN] Forces between rollers and guides [kN]](images/7pic8.png)
Fig. 4.b – Forces between rollers and guides [kN]
Fig. 4. Influence of clearance or preliminary thrust between rollers and guides (D1..D3 - 2,-2,5 mm) on stresses in cage beams and forces in rollers
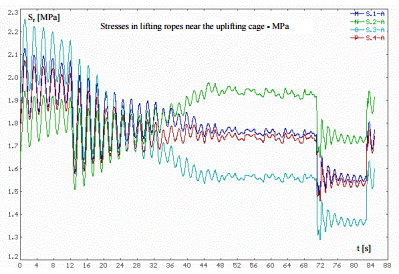
Fig. 5. Example of great variations of load carried by individual ropes (1..4) during the motion of cage from lower to higher level
8. References
- Cock M. J. L.,
Winder Control Technology for the reduction of Dynamic Rope Stresses
, ‘Mining 94’ Conference, Birmingham 1994. - Gerlach A., Horstmann R.,
Seilrutsverhalten von Treibscheibenanlagen unter berucksichtigung dynamischer Vorgange
, Gluckauf-Forschungshefte 54, nr 5, 1993. - Hansel J.,
New methods of designing of hoisting cages and shaft reinforcement
Rozprawy, Monografie AGH, z.16, Krakow 1994. (in Polish). - Potts A.,
From top to bottom
, World Mining Equipment, 10.1998, 26–30. - Tejszerska D.,
Modelling of coupled transverse–longitudinal vibrations of hoisting systems
, ZN Pol.Sl, Mechanika, z.124, 93 pg, Gliwice 1995 (in Polish). - Tejszerska D.,
Computer analysis of vibrations of hoisting system
, Comp.Assist.Mech. &Eng.Sci, vol 4, No 2, 179–188, 1997. - Vondrak I., Sabela Z.,
Computer modeling of hoist dynamics and its verification
, Uhli, 37, nr 8, s. 362–367, 1989 (in Czech).