1. Введение
Исследование графа роботами. Проблема исследования графа состоит в посещении одного или нескольких роботов-существ каждой вершины связного графа. Эти мобильные существа иногда называют агентами или роботами. Поэтому мы используем слово «Робот». Обход графа бесконечен, если робот бесконечное число раз посещает каждую вершину графа. Бесконечное исследование графа не избежать, когда роботы должны двигаться вместе, непрерывно отправляя информацию или ища динамические ресурсы (ресурсы, чье положение меняется с изменением времени). Если узлы и ребра имеют уникальные названия, обход графа относительно проще и не бесконечен.
Проблема обхода графа становится более серьезной, когда граф неизвестный ([6,10,12] то есть, вершины и ребра графа не имеют маркеров). В таком контексте, устанавливают некоторые ограничения. Они касаются времени на посещение вершин, или размера памяти робота, необходимой для исследования графа (например, это доказано в [8], когда робот нуждается в O(D log d) битах локальной памяти для последовательного исследования любого графа размерностью и максимальной связностью d. Результаты невозможны для одного или нескольких роботов с ограниченной памятью (вычислительная сложность робота определена, когда определена степень автоматизации) для исследования всех графов, указанных в [5, 14]. Главная часть результатов по исследованию графов выполнена с учетом того, что обход графа делается одним роботом. Только в последнее время обход (исследование) графа несколькими роботами стало популярным. Это мотивировано исследованиями на более эффективных (подготовленных) графах, с допустимыми дефектами, или нуждающихся в ослаблении точности для ограниченных возможностей одного робота.
Неизбежные проблемы при исследовании графа. В этом документе рассмотрена проблема бесконечного обхода графа, называемая кратко от англ. CPGE. Рассматривается максимальное количество роботов, которые обладают разрешимостью. В каждый робот посещает весь граф бесконечное число раз все время, избегая остальных роботов, в некоторой вершине они могут столкнуться или пересечься на некотором ребре. Эта дополнительная проблема является абстрактной проблемой коллизий, которую роботы могут навлечь на себя, когда движутся на короткой дистанции между каждым из роботов или при потребности роботов принять ресурсы, принадлежащие обеим сторонам, возникает исключающий конфликт. Это условие ограничивает движение роботов на карте.
Результат в статье показывает проблему верхней границы k на числе роботов, которые имеют разрешимость CPGE-проблемы на неизвестном связном графе. Чтобы достичь невозможного результата такой точности, насколько это возможно, модель рассматриваемых вычислений довольно точная, а именно синхронная система движения роботов может быть требованием для всезнающих сущностей (роботов). Не удивительно, что верхняя граница относится к структуре графа (легко понять, что если граф является цепью, то посетить все вершины от начальной к конечной без конфликтов удастся только одному роботу).
Карта документа.Документ состоит из 6 разделов. Раздел 2 представляет модель вычислений, в то время как раздел 3 вводит в проблему CPGE. В разделе 4 представлены существующие работы. Затем в разделе 5 предлагается и доказывается оценка на максимальном количестве роботов, которые могут одновременно решить проблему CPGE. С этой целью, вводится процедура редукции из графа с меченым деревом. Это дерево охватывает простой путь графа, по которому должен пройти один робот. Длина самой длинной из этих меченых путей затем дает нам верхнюю границу количества роботов. Наконец, в разделе 6 вывод по статье.
2. Модель
Система состоит из конечного связного неориентированного графа G=(S,E) и конечного множества R роботов таких, что |R|<=|S|. Граф является неизвестным в том смысле, что вершины не имеют маркеров на вершинах. Роботы имеют общие часы, а время делится на синхронные раунды [14]. В каждом раунде робот может двигаться от вершины, где оннастоящее время находится, к соседней вершине или остается в той же вершине. Движение робота от вершины к соседней вершине делается за один шаг. Свойство является таковым, что на вершине одновременно существует только один робот.
Путь роботов определяется всезнающим мастером, у которого вычислительная мощность как у машины Тьюринга, т.е. бесконечна. Этот всезнающий мастер представляет возможности роботов, а также глобально синхронизирует передвижение роботов. Всезнающий мастер (эксперт) обеспечивает каждого робота с (1) карты графа (2) в исходное положение каждого робота (3) программой эксперта, и позволяет каждому роботу имитировать поведение эксперта.
Определение 1: Дан робот a и раунд r, V (a, r) обозначает (единственную) вершину, где робот расположен в начале раунда r.
3.Проблема бесконечного исследования графа (CPGE)
Как уже отмечалось, CPGE состоит в проектировании алгоритма для действий каждого робота, чтобы посетить каждую вершину графа, таким образом, чтобы никакие два робота не находились в одной вершине одновременно, и во время каждого раунда никакие два робота не углублялись в тот же самый путь. Это может быть формально определено следующими тремя свойствами.
1.Бесконечное исследование

Для любой вершины v и любого робота a, есть бесконечно много раундов для посещения v вершины.
2. Взаимное исключение вершин.

В начале любого раунда никакие два робота не находятся в одной и той же вершине.
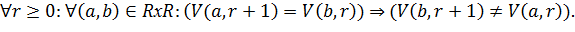
3. Взаимное исключение ребер
Во время раунда никакие два робота не углубляются по одному и тому же ребру (т.е., они не могут изменять свои положения).
4. Взаимодействие работы
Начальные предположения. Как уже обозначено, исследование графа – процесс, в котором каждая вершина графа посещается некоторым существом (роботом агентом). Большая научно-исследовательская работа по исследованию графа роботами была основана на минимальных предположениях (в условиях требований роботов или сети), требуемых для исследования графа (например, [3, 8]). Некоторые работы сосредотачиваются на роботах, обеспеченных постоянным хранением информации и непосредственной связью с другими роботами (например, [2]). Некоторые научные работы предполагают, что каждый робот имеет способность видеть, куда другие роботы в настоящее время перемещаются (например, [6]). Другие работы изучают карты (граф) с роботами, уменьшая сложность исследования (например, [12]).
В нашей работе все эти предположения (на возможностях роботов или на начальном знании) направлены на всезнающего мастера (агента экспериментатора), который управляет движением робота на графе.
О типах исследования графов. Исследование графа, главным образом, разделено на бесконечное исследование графа (например, [5]), где роботы должны двигаться по графу бесконечное число раз, а также исследование графа с остановкой (например, [8]), где каждый робот должен, в конечном счете, остановиться, исследовав граф. Некоторые работы фокусируются на исследовании графа одним роботом (например, [1, 2, 7]). Совместное исследование графа командой мобильных роботов также получило внимание (например,[3, 6, 10]). Например, исследования мульти робота, это показывают в [6], что минимальное число роботов требуемых для решения задачи исследования с остановкой на раунде размера n O(log n), когда исследование сделано роботом асинхронно, не используя памяти робота.
Более низкие границы были установлены для проблемы бесконечного исследования графа (например, [5, 9]). Эти границы касаются периода, необходимого для робота, чтобы закончить посещение графа, принимая ограничения для любого робота или графа. Другими словами, верхняя граница, введенная в этой статье, касается максимального количества роботов, которые могут посещать граф бесконечно часто без столкновений.
Исследование графа сограничениями. Как уже замечено, проблема CPGE, определенная в разделе 3, проблема бесконечного исследования графа увеличилась в связи с взаимным исключением на вершинах и ребрах графа. Эти взаимные ограничения исключения были уже заявлены и использовались в [10], где графы, которые рассматриваются, являются сетками. Проблема, решенная в той статье, отличается от CPGE. Точнее, в [10] каждый робот должен посетить некоторую цель у вершин сетки и у любых двух отличных роботов это различные цели. Та статья устанавливает более низкие границы, привязка времени (число раундов в синхронной системе) необходимы, чтобы решить ту проблему и представить оптимальный алгоритм. Проблема столкновения роботов также рассматривалась в [15], где предложен алгоритм предотвращения столкновения роботов, углубляющихся на плоскости.
5. Верхняя граница числа роботов
Дан граф G, пусть k - максимальное число роботов, для которых может быть решена проблема CPGE. Понятие проблемы разрешимости, используемое здесь, является (как уже обозначено) у того всезнающего мастера, который знает граф и настоящее положение роботов, и определяет для каждого раунда поведение каждого робота. Как замечено во Введении, проблема разрешимости имеет очень сильное влияние, а именно, даже с таким мастером невозможно решить CPGE с больше, чем k роботами.
Легко увидеть, что топология графа устанавливает естественно привязанное число роботов, которые решают разрешимость CPGE. Дело обстоит для любого простого графа, который является цепью. В этом типе графа, CPGE может быть решена, когда максимальное число роботов = 1. В противовес, CPGE может тривиально быть решенный с n роботами в кольце размера n (всезнающий мастер сначала определяет умение ориентироваться на цепи, и затем, неоднократно в каждом раунде, направляет каждого робота, чтобы двинуться в следующую вершину).
В то время как определение максимального номера k роботов, для которых может быть решена CPGE, очень легко определить для некоторых графов, это далеко от того, чтобы охватить все топологические особенности графа, которые позволяют оценить верхнюю границу k. С этой целью статья вводит процедуру сокращения, которая преобразовывает любой граф в маркированное дерево (названное деревом мобильности), от которого может быть определена величина k. Это дерево охватывает пути, которые должны быть пересечены, a один робот должен проходить за один раз.
5.1. Предварительные определения
Далее мы рассматриваем только неориентированные связанные графы, без дуг и петель. Вершина v является листом графа G = (S; E), если есть единственная вершина v1 такая, что (v,v1) E. Степень d вершины v является целым числом. Мост – это ребро, удаление которого разъединяет граф. Граф без моста безмостовой граф. Путь от вершины v к вершине v1 прост, если никакая вершина не появляется на нем больше чем один раз.
Граф G1=(S1,E1), подграф графа G=(S,E), если S1 S и E1 E. В этом случае мы также говорим это G=(S,E) суперграф G1=(S1,E1). Неединичный подграф содержит, по крайней мере, две вершины. Подграф G1=(S1,E1), состоит из набора вершин S1, если E1 содержит все края E, конечные точки которого находятся в S1. Далее будем рассматривать все подграфы, которые будут являются вызванными подграфами, мы опускаем термин “вызванный” чтобы не перегружать статью.
Подграф G1 максимален относительно условия P, если G1 удовлетворяет P, в то время, как ни один из суперграфов не удовлетворяет P. Так, “безмостовой” и “неединичный” – свойства, которым подграф удовлетворяет или не удовлетворяет.
5.2.От графа к дереву: процедура сокращения
Определение 2. (Дерево мобильности). Пусть маркированное дерево мобильности связано с графом G=(S, E), который будет маркированным деревом G1 = (S1; E1), который произошел от G до процедуры сокращения выполняем следующие действия:
1.Начальная маркировка. Каждая вершина v G сначала маркируется следующим образом:
– Маркер 0: если v не принадлежит подграфу G, то его степень равняется двум;
– Маркер 1: если v – лист G или принадлежит неединичному подграфу G;
– Маркер 2: иначе.
2. Сжатие. Каждый максимальный неединичный безмостовой подграф G сокращается до вершины с маркером 1.
Рисунок 1 показывает пример процедуры сокращения. Граф G изображен на рисунке 1 (a). Результат начальной маркировки его вершин представлен на рисунке 1 (b).
Неединичные подграфы G обведены кругами. Наконец, маркированное дерево мобильности, полученное из сжатия неединичных подграфов показано на рисунке 1 (c).
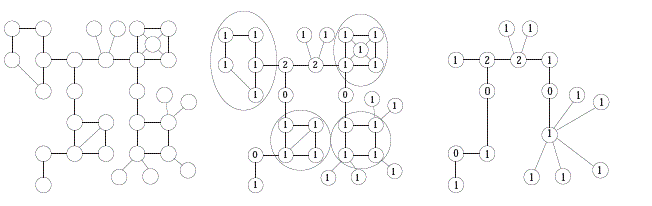
Рисунок 1 – граф G и маркированное дерево мобильности G
Дерево мобильности графа G предназначено, для того чтобы уделить внимание особенностям графа G при разрешимости CPGE проблемы. Во-первых, это указывает на те подграфы G (соответствующие вершинам с Маркером 1 на дереве мобильности), где CPGE могла бы быть решена в каждом из таких подграфов в изоляции со другими роботами, равными числу вершин подграфа. Во-вторых, дерево мобильности показывает те пути графа G, которые должны быть пересечены одним роботом за один раз, чтобы переместиться от одного из предыдущих подграфов G к другому, расширяя разрешимость CPGE в графе G. Поэтому вводим понятие Взаимного Пути Исключения.
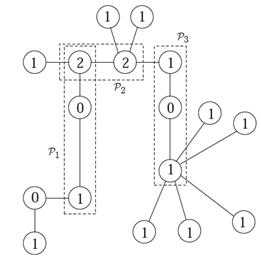
Рисунок 2 – Пример взаимных путей исключения в дереве мобильности
Определение 3. (Взаимный Путь Исключения) Пусть P путь (v,v1), (v1, v2) …(vm, v/) дерево подвижности G/ от вершины v к v/. P - взаимный путь исключения G/ если:
– маркеры v и v/ отличные от 0;
– если есть вершины, (т.е., путь от v до v/ содержит больше чем одно ребро), то те вершины маркируются 0.
Например, рисунок 2 показывает три взаимных пути исключения, P1, P2 и P3, на маркированном дереве мобильности представленном на рисунке 1 (c).
Определение 4. (Длина Взаимного пути Исключения) В маркированном дереве мобильности G1=(S1,E1), пусть длина Взаимного исключения Пути между любыми двумя вершинами v, v/ G/ - число ребер от v до v/.
Длина P1, изображенного на рисунке 2, равняется 2+j=3 (при j=1). Длина P2 равняется 1+j=3 (при j=2) в то время как длина P3 равняется 2+0=2 (при j=0). Интуитивно понятно, что длина взаимного пути исключения представляет минимум число вершин, которые должны быть первоначально пустыми (т.е. без маркировки роботом) с целью, чтобы роботы были в состоянии решить проблему CPGE относительно своего пути. Поэтому вычислять максимальную длину взаимных путей исключения становится ключевым фактором, чтобы вычислить верхнюю границу числа роботов, при решении разрешимости CPGE в графе G.
Определение 5. Для любого p>0 и q>=0, пусть GG(p,q) набор графов, таким образом, что для любого G∈GG(p,q) мы имеем:
– у графа G p вершин;
– q – максимальная длина взаимных путей исключения дерева мобильности, связного с графом G.
Два графа принадлежат одному и тому же классу GG(p,q), если у них обоих есть одинаковое число вершин p и максимальная длина q взаимного пути исключения их соответствующих деревьев мобильности. Поскольку мы собираемся рассмотреть этот вопрос в следующей секции, максимальное число роботов, для которых проблема CPGE может быть разрешена в любом графе в GG(p,q) это k=p-q.
5.3. Верхняя граница
Теорема 1. Пусть G – граф класса GG(p,q). Не существует алгоритма, который решает CPGE для G от произвольной конфигурации, включая более чем k= p-q роботов.
Доказательство. Доказательство противоречием. Давайте предполагать, что есть алгоритм, который решает CPGE для графа G∈GG(p,q) и любая начальная конфигурация,по крайней мере, с p – q+1 роботами. Нет никакого ограничения на A: его вычислительное способность - та машины Тьюринга с неограниченной памятью.
Противоречие для случая q = 0 очевидно: не возможно поместить p + 1 роботов на графе с p вершинам не нарушая свойства взаимного исключения вершины. Так, остальная часть доказательства рассматривает q>0.
Давайте отметим, что из-за свойства вершины о взаимном исключении, любая конфигурация, достижимая от начальной конфигурация, содержит q-1 вершины без роботов. Согласно определению GG(p,q), q - максимальная длина из взаимных путей исключения дерева мобильности G. Пусть u - такой путь, с X и Y - координаты его конечной вершины. Согласно маркерам X и Y, можно отличить три случая (но благодаря маркированной мобильности абстракции графа, рассуждение просто и идентично во всех случаях)
– и X и Y имеют маркер 1. Это означает, если путь от X до Y в G содержит больше чем одно ребро, то вершины, отличающиеся от X и Y, имеют степень 2 и маркированы 0.
– пусть GX и GY - максимальные подграфы графа G, который включают X и Y, соответственно, и удовлетворяют следующему свойству P: любой простой путь в G от любого v∈GX до любых v/∈GY, включая и X и Y. (См. иллюстрацию на рисунке 3) Как X так и Y имеют маркер 1, это следует из Определения 4, что u - последовательность q + 1 вершин (и, как уже видно, у каждой вершины в этой последовательности, отличающейся от X и Y, есть степень 2).
Давайте рассматривать начальную конфигурацию, где q - 1 вершин без роботов являются точно вершинами u\ {X,Y}. Затем p-(q-1) роботов заполняют полностью все вершины подграфов GX и GY. Как только q-1 вершин окажется без роботов (вершины u \ {X,Y}), из этого следует, что никакой робот в вершине v∈GX не может переместиться в вершину v/∈GY (или наоборот), не нарушая свойства взаимного исключения вершины или свойства взаимного исключения ребра, которые доказывают теорему для этого случая.
X и Y имеют маркер 2 и 1, соответственно. Мы завершаем: из Определения 4 и маркеров X и Y следует, что путь u является последовательностью q вершин. Пусть G1X, G2X (и возможно G3X, G4X, …) обозначают максимальные подграфы G, которые не содержат X и любой путь в G от любой вершины v G1X G2X к любой вершине v/ GY (где GY включает Y), включает и X и Y (см. рис. 4).
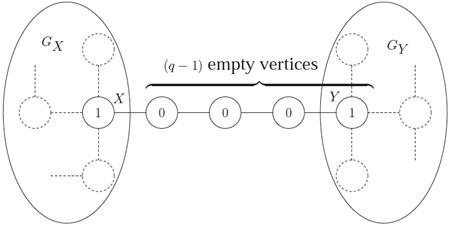
Рисунок 3 – взаимные пути исключения в дереве мобильности от маркера 1 к маркеру 1, при q=4
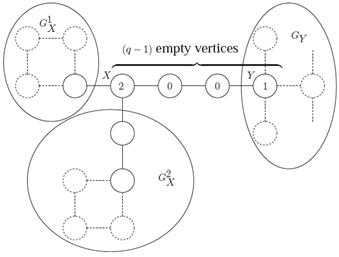
Рисунок 4 – взаимные пути исключения в дереве мобильности от маркера 1 к маркеру 2, при q=4
Эта статья исследовала проблему бесконечного исследования графа Ограниченную (CPGE). Эта проблема состоит в создании как можно больше мобильных существ (роботов), чтобы посещать бесконечно долго каждую вершину неориентированного связного графа, при ограничении, что два робота не могут быть одновременно в одной и той же самой вершине, ни одновременно пойти по одному и тому же ребру. Статья установила верхнюю границу числа роботов, для которых может быть решена CPGE.
Сделав результат максимально эффективным, было доказано, что роботы ведут себя синхронно, и их движения скоординированы всезнающим мастером (экспертом). Было показано, что эта верхняя граница связана с топологической структурой графа, который нужно исследовать, таким образом, определяя классы графов и наличие той же самой верхней границы.
Открытой остается интересная проблема, которая состоит в очистке этой верхней границы, когда у каждого робота есть ограниченная память, или когда его текущие знания ограничены частью графа (положение определятся динамично в каждом раунде от настоящего положения робота на графе).