Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Модель автомата
- 4. Задача анализа влияния локальных преобразований на поведения конечных автоматов
- 5. Приведение теоретических результатов
- Выводы
- Список источников
Введение
Использование модели конечных автоматов для описания различных дискретных систем и процессах является самым практичным методом их представления. Однако для полного представления необходимо учитывать факт возможности воздействия внешних факторов, способных изменить поведение конечного автомата и всей системы в целом. Воздействием можно считать любое локальное преобразование над исходным состоянием автомата. В виду этого возникает необходимость провести анализ поведения двух состояний автомата исходного и преобразованного и сравнить их. В данной работе исследуется поведения конечного автомата при локальных преобразованиях.
1. Актуальность темы
Модель конечного автомата может быть полезна при описании различных типов взаимодействия объектов, как при технических задачах построения управляющих систем, так и при задачах описания поведения любых объектов, где требуется изучить понятия состояние, воздействия входного параметра и как результат – реакции на него. Так теория автоматов применяется в разработке формальных языков и языков программирования, а также в программировании при непосредственном написании программ, в так называемом автоматном программировании. В практическом смысле реализация конечного автомата есть в любом вычислительном устройстве.
Поэтому актуальность исследование модели конечных автоматов очевидна, и как следствие, важно и исследование поведения конечного автомата при локальных преобразованиях.
2. Цель и задачи исследования, планируемые результаты
Целью исследования является разработка и исследование метода оценки влияния локальных преобразований на поведение конечного автомата.
Основные задачи исследования:
- Проанализировать поведение автоматов исходного и порождаемого преобразованиями, полученными из-за переброски дуг.
- Оценить степень близости для любой переброски дуг.
- Составить описание структуры класса локально порождённых автоматов, разбивая его на подклассы автоматов, которые будут эквивалентны по мере близости их поведения поведению исходно заданного автомата.
Объект исследования: поведения конечного приведенного автомата при локальных преобразованиях.
Предмет исследования: нахождение степени близости поведения исходного автомата и автомата, полученного в результате воздействия локального преобразования в виде некоторой последовательности перебросок дуг в графе переходов исходного автомата.
3. Модель автомата
Проведем сравнение поведения автоматов при локальных преобразованиях, получаемых в результате перебросок дуг, возьмем частный случай: в качестве исходного автомата будем рассматривать определенно диагностируемый порядка k автомат, а под локальным преобразованием будем понимать переброску ровно одной дуги.
Автомат Мили A = (S, X, Y, δ, λ, s0) будет использован как инициальный приведенный ОД-k, в котором S - это конечное множество состояний, X, Y – конечные множества входных и выходных, δ, λ – это функции переходов и выходов, и s0 принято за начальное состояние. Индекс А или значок штриха добавлен к обозначениям этих объектов при необходимости для избежания путаницы.
Автомат А называется определенно диагностируемым автоматом порядка k, если k≥1 – наименьшее целое такое, что для любого входного слова p длины k и любой пары различных состояний s,t∈S выполняется неравенство λ(s,p)≠λ'(t,p).
Эквивалентными называются два состояния s и t одного и того же автомата A или двух разных автоматов A и B соответственно, если для любого входного слова р∈X* будет выполнено условие λ(a,p)=λ'(b,p), где λ' – функция выходов автомата A или B. Приведенный автомат называется таким образом при условии, если все его состояния попарно неэквивалентны.
Функции δ и λ распространяются обычным образом на множество X* всех входных слов конечной длины в автомате.
Пусть w=(p,q) - вход–выходное слово, оно порождается состоянием s автомата А, если λ(s,р)=q. Длина слова w будет обозначена |w|.
Для каждому состоянию s в соответствие поставим множество λs всех вход–выходных слов, которые порождаются попарно неэквивалентными состояниями автомата. Поведение автомата А будем пониматься под множеством λs0 вход–выходных слов, которые порождаются его начальным состоянием.
Наиболее удобным будет задать автомат в виде графа переходов, у которого вершины будут соответствовать состояниям из S, а дуги будут являться четверками (s,x,y,t), при t=δ(s,x), y=λ(s,x). Отметкой дуги называется пара (x,y), начало дуги – s, конец дуги – t. При e=(t,x,y,u) – дуга в графе переходов автомата A, переброска этой дуги из состояния u в состояние v, отличное от u, будет называться заменой её следующей дугой – (t,x,y,v).
4. Задача анализа влияния локальных преобразований на поведения конечных автоматов
Исследование автоматы, близких по поведению в том или ином смысле, а также структура их классов [1], продолжается довольно давно, в основном благодаря развитию теории экспериментов с автоматами. Основание теории экспериментов с автоматами было положено Муром [12], тогда был впервые предложен алгоритм определения эквивалентности автоматов.
Работы А. Гилла [1], Ф. Хенни, М.П. Василевского, A.M. Богомолова [10], И.С. Грунского [2,3,8], С.В. Яблонского, И.К. Рысцова, Н.В. Евтушенко, В.А. Твердохлебова , А.Ф. Петренко, а также многих других посвящены теории экспериментов.
Сейчас теория экспериментов продолжает и далее свое интенсивное развитие среди научных деятелей, при исследовании влияния локальных преобразований на поведения автоматов, получено немаловажные результатов. Именно влияние перебросок дуг на графе переходов автомата на поведение автомата приведено в [3-7, 9]. Изучив эти работы, обнаружены такие выводы:
- в приведенном автомате переброска ровно одной дуги всегда вызывает изменение поведения автомата, которое становится неэквивалентным исходному приведенному автомату;
- при переброске одной дуги всегда получается неизоморфный автомат;
- при переброске двух дуг может получиться автомат, эквивалентный исходному;
- при переброске двух дуг входные-выходные отметки на перебрасываемых дугах должны совпадать;
- переброска более двух дуг возможна, при условии, когда входные–выходные отметки на перебрасываемых дугах различны;
- существует такая структура автоматов, где в графах автоматов, имеющие не достаточно сильные связи, к возможна переброска ≥ 2 дуг;
- при осуществлении ≥ 4–х перебросок в некоторых существующих сильно связанных автоматах сохраняется изоморфизм;
- переброска дуг, сохраняющая изоморфизм, возможна в автоматах, обладающих определенной симметрией графа переходов, которая отражается и в циклической структуре графа;
- сохранять изоморфизм при переброске дуг могут автоматы, которые обладают определенной симметрией графа переходов, отражающейся и в циклической структуре графа.
5. Приведение теоретических результатов
Рассмотрим структуру локально порожденного класса. Следующая теорема показывает, как связано расстояние между двумя локально порождёнными автоматами и два параметра: d – длина кратчайшего слова, которое переводит автомат из начального состояния в состояние из которого будет переброшена дуга , и k – параметр ОДk-автомата.
Теорема 5.1. Пусть А – инициальный приведенный ОД-k-автомат и A' получен из А переброской дуги (t,x,y,u) в состояние v. Тогда ρ(A,A')≥1/(d+k+1), где d – длина кратчайшего входного слова w такого, что δ(s0,w)=t.
Доказательство. Чтобы отличать состояния автомата А от состояний A', будем состояния последнего помечать штрихом и пару (s,s') называть двойственными, где s∈S, s'∈S'. Покажем сначала, что состояния u и v' различимы некоторым словом длины, не большей k. Для этого воспользуемся приёмом, использованным при доказательстве того факта, что переброска дуги в любом приведенном автомате всегда приводит к автомату, не изоморфному исходному [7]. Построим автомат В, равный прямой сумме автоматов А и А', и рассмотрим процесс построения Рi-таблиц [11] для автомата В.
Поскольку таблицы выходов автоматов А и А' совпадают, то в таблице Р1 каждый класс эквивалентности состоит из пар двойственных состояний.
Заметим, что любая пара (s,s'), кроме пары (t,t'), по любому х опять переходит в пару двойственных состояний. Пара (t,t') – единственная, для
которой это не выполняется, так как δB(t,x)=u и δB(t',x)=v'. Отсюда следует, что пока состояния (t,t') k-эквивалентны, любая пара (s,s'),
отличная от (t,t'), будет (k+1)-эквивалентной. Сама же пара (t,t') k-эквивалентна, пока пара (u,v') является (k-1)-эквивалентной. Но, если
(u,v') (k-1)-эквивалентна, то тогда пары (t,t'), (u,u'), (v,v') k-эквивалентны и, значит, состояния u, u', v, v' принадлежат одному классу
эквивалентности в таблице Рk. Так как А ОД-k-автомат, то для некоторого i Пусть теперь w – кратчайшее входное слово в автомате А, переводящее его из начального состояния в состояние t, и р – кратчайшее слово,
различающее u и v'. Пусть |w|=d,|p|=i, и как показано выше, i≤k. Ясно, что в автомате А' δ(s'0,w)=t'. Тогда δ(s0,wx)=u, δ(s'0,wx)=v',
λ(s0,wx)=λ(s'0,wx), но λ(s0,wxp)≠λ(s'0,wxp), причём |wxp|≤d+1+k, что и требовалось доказать. Покажем, что полученная оценка расстояния достижима. На рисунке 5.1 приведен инициальный автономный автомат А. Пусть автомат А'
является результатом переброски одной дуги в автомате А: дуга (6,0,2,5) перебрасывается в состояние 3 и заменяется дугой (6',0,2,3').
Поскольку перебрасывается дуга, исходящая из состояния 6, то кратчайшее слово w имеет длину d=3. Легко видеть, что λ(s0,0000)=λ(s'0,0000),
но λ(s0,00000)≠λ(s'0,00000). Поэтому wxp=00000 и |wxp|=5. Отсюда ρ(A,A')=1/5. На примере видно, что в результате переброски дуги автомат
A' стал приведенным автоматом, так как состояния 5 и 6 стали эквивалентными. Рисунок 5.1 – Пример переброски одной дуги в автомате ОД-2 Теорема 5.2. Пусть А – инициальный приведенный автомат и A' получен из А переброской дуги (t,x,y,u) в состояние v. Тогда
ρ(A,A')≥1/(d+n), где d – длина кратчайшего входного слова w такого, что δ(s0,w)=t. Теорема 5.3. Класс Ki (A)состоит из всех тех автоматов А', для которых выполняется следующее условие: d+с+1=i. Полный доказательства теоремы 5.2 и теоремы 5.3 будет приведено в тексте магистерской работы. В данной работе были получены такие результаты: При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2015 года. Полный
текст работы и материалы по теме могут быть получены у автора или его научного руководителя после указанной даты.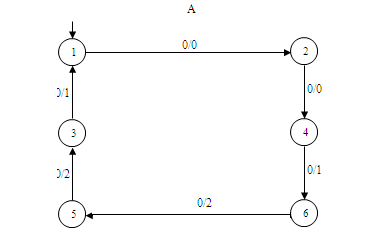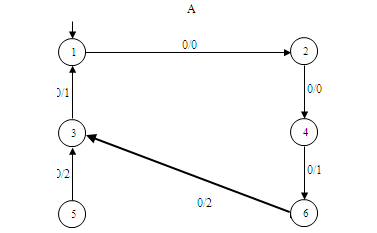
(анимация: 2 кадров, 7 циклов повторения, размер - 377×233, 5,22 килобайт)Выводы
Список источников
Дискретные модели в теории управляющих систем
. – М.: Макс–Пресс, 2009, C. 150–158.
