Реферат за темою випускної роботи
Зміст
- Вступ
- 1 Актуальність теми
- 2 Мета і задачі дослідження та заплановані результати
- 3 Основні поняття і властивості контурів
- 3.1 Поняття контур
- 3.2 Властивості контурів
- 3.3 Скалярне множення контурів
- 3.4 Кореляційні функції контурів
- 3.5 Автокорреляційна функція
- 3.6 Загальний алгоритм розпізнавання
- 3.7 Оцінка продуктивності алгоритмів у контурному аналізі
- 3.8 Дескриптор контура
- 3.9 Згортка автокорреляціїної функції
- 3.10 Еквалізація контурів
- Висновки
- Список використаних джерел
Вступ
З розвитком обчислювальної техніки стало можливим вирішувати завдання, які раніше вважалися нездійсненними на персональних комп'ютерах. Створення пристроїв, що виконують функції розпізнавання об'єктів у відеопотоці, в більшості випадків дозволить замінити людину–спеціалізованим автоматом. Варто зауважити, що якість виконання роботи людиною залежить від багатьох факторів (кваліфікація, досвід, втома, інтерес). Водночас справна і налаштована система працюватиме, забезпечуючи завжди однакову якість виконання роботи. Ще одним плюсом заміщення людини машиною - незрівняне перевагу автоматичних систем у швидкодії.
На сьогоднішній день в кожному місті та мегаполісі існує транспортні затори, які в пікові години досягають сотень кілометрів, наземний громадський
транспорт значно знижує свою провізну можливість і стає малопривабливим для пасажирів, ускладнюеться пересування екстреного і службового транспорту,
зростає кількість дрібних аварій, порушень ПДР, від стоячих і працюючих на самому шкідливому
холостому ходу автомобілів збільшується загазованість
повітря і т. п.
Основна причина транспортної проблеми полягає у початковії плануванні міста без урахування можливостей широкого використання особистих автомобілів. Планування вулиць, наприклад, у Москві радіально-кільцева і теоретично має важливу перевагу перед прямокутної (як, наприклад, в Нью-Йорку), оскільки за рахунок діагональних маршрутів вона мінімізує час переміщення по місту. Але на практиці така конфігурація доріг призводить до того, що центр міста, що з'єднує радіальні магістралі, часто перетворюється на один суцільний затор.
1 Актуальність теми
Методи контурного аналізу в сучасності досить широко застосовуються в радіотехнічних системах, в системах зв'язку, для орієнтації літальних апаратів [1], в процесі контролю за пересуванням автомобілів, для детектування номерів машин, контролю швидкості або порушень правил дорожнього руху [2]. Контур - це найбільш інформативний структурний елемент об'єкта. Однак якісне виділення контуру – це одна з найскладніших проблем обробки візуальної інформації. Відомі методи вирішення завдань контурного аналізу за допомогою бібліотеки OpenCV, але цей пакет призначений для вирішення завдання підрахунку об'єктів, що мають візуально помітну крапку на зображенні. А контури часто мають такі недоліки, як розриви, наявність зайвих ліній, які не відповідають досліджуваному об'єкту.
Тому створення і впровадження програмного забезпечення для контролю автомобільного транспорту дозволить контролювати пропускну спроможність доріг і вирішити проблему освіти транспортних пробок. Дана система буде взаємодіяти з світлофором, при включенні на світлофорі червоного кольору буде робитися знімок дороги і буде аналізуватися кількість машин на знімку.
2. Мета і задачі дослідження та заплановані результати
Мета данної кваліфікаційної роботи –розробка програмного забезпечення контролю автомобільного трафіку.
Об’єкт розробки – програмне забезпечення, що забезпечує контроль автомобільного трафіку шляхом контурного аналізу зображень стану проїжджої частини дороги, що отримано з камер спостереження.
Предмет розробки – сучасні засоби проектування та розробки програмного забезпечення: MS Visio 2013, мова С#, середовище розробки MS Visual Studio 2012.
Для досягнення поставленої мети необхідно вирішити наступні задачі:
1) провести огляд існуючих систем;
2) розглянути основні принципи побудови алгоритмів контурного аналізу, проаналізувати оцінку їх продуктивності;
3) вибір оптимального алгоритму для реалізації системи;
4) обґрунтування мови програмування і середовища розробки;
5) спроектувати архітектуру системи;
6) розробити програмне забезпечення системи.
3 Поняття контур
Контурний аналіз дозволяє описувати, зберігати, порівнювати і робити пошук об'єктів, представлених у вигляді своїх зовнішніх обрисів – контурів. Контур – це кордон об'єкта, сукупність точок (пікселів), що відокремлюють об'єкт від фону. Передбачається, що контур містить всю необхідну інформацію про форму об'єкта [3]. Внутрішні точки об'єкта до уваги не приймаються. Це обмежує область застосовності алгоритмів контурного аналізу, але розгляд тільки контурів дозволяє перейти від двовимірного простору зображення – до простору контурів, і тим самим знизити обчислювальну та алгоритмічну складність. Контурний аналіз дозволяє ефективно вирішувати основні проблеми розпізнавання образів – перенесення, поворот і зміна масштабу зображення об'єкта.
У системах комп'ютерного зору використовується декілька способів кодування контуру – найбільш відомі код Фрімена, двовимірне кодування, полігональне кодування. Але всі ці способи кодування не використовуються в контурному аналізі. Замість цього, в контурному аналізі контур кодується послідовністю, що складається з комплексних чисел. На контурі фіксується точка, яка називається початковою точкою. Потім, контур обходиться (припустимо – за годинниковою стрілкою, див. рис. 1), і кожен вектор зміщення записується комплексним числом a + ib. Де a – зсув точки по осі Ох, а b – зсув по осі Оy. Зсув береться щодо попередньої точки.
В силу фізичної природи тривимірних об'єктів, їх контури завжди замкнені і не можуть мати самопересеченія. Це дозволяє однозначно визначити шлях обходу контуру (з точністю до напрямку за або проти годинникової стрілки). Останній вектор контуру завжди приводить до початкової точки. Операції над контуром саме як над вектором комплексних чисел володіє чудовими математичними властивостями, в порівнянні з іншими способами кодування.
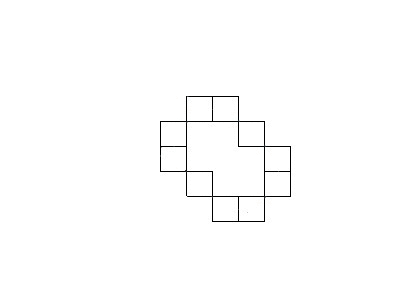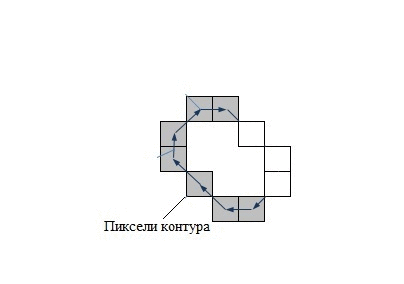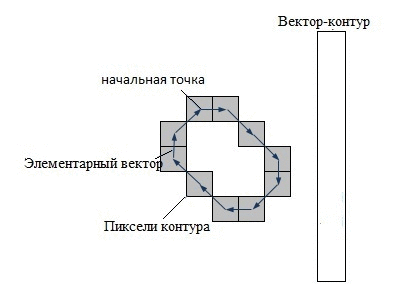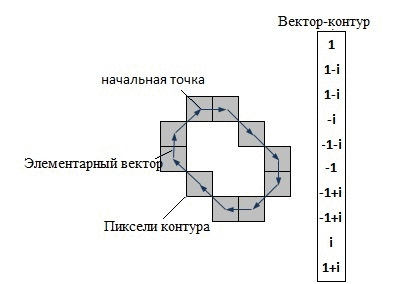
Рисунок 1 – Кодирование контура (анимация: 7 кадров, 15 циклов повторения, 74 килобайта)
Комплексне кодування близько до двовимірному кодуванню, де контур визначається як сукупність елементарних векторів, представлених своїми двовимірними координатами. Різниця полягая в різниці операції скалярного множення для векторів і для комплексних чисел, що надає перевагу методам контурного аналізу.
3.2 Свойства контуров
Розглянемо властивосі контурів.
1. Сума елементарних векторів замкнутого контуру дорівнює нулю. Оскільки елементарні вектори призводять в початкову точку, їх сума дорівнює нульовому вектору.
2. Контур–вектор не залежить від паралельного перенесення вихідного зображення. Оскільки контур кодується щодо початкової точки, цей засіб кодування інваріантний зрушенню вихідного контуру.
3. Поворот зображення на певний кут рівносильний повороту кожного елементарного вектору контуру на той же кут.
4. Зміна початкової точки веде до циклічного зсуву вектору контура. Оскільки елементарним вектором кодуються щодо попередньої точки, то при зміні початкової точки послідовність елементарного вектора буде та ж сама, але першим елементарним вектором буде той, котрий починається в початковій точці.
5. Зміна масштабу вихідного зображення можна розгладати як множення кожного елементарного вектора контура на масштабний коефіцієнт.
3.3 Скалярне множення контурів
Скалярним множенням контурів Г і N називається таке комплексне число:
η = (Г, N) = ∑(k-1) n=0(Yn,Vn)
де: k – розмірність ВК;
Yn – n-й елементарний вектор контуру Г;
Vn – n-й ЕВ контуру N;
(Yn, Vn) – скалярний добуток комплексних чисел, що обчислюється наступним чином:
(a + ib, c + id) = (a + ib) (c – id) = ac + bd + i (bc – ad).
В контурному аналізі допускається скалярне множення тільки ВК однакової розмірності, тобто, число елементарних векторів в контурах повинно збігатися [4].
Скалярне множення звичайних векторів і скалярне множення комплексних чисел – відрізняються. Перемноження ЕВ як простих векторів дає скалярний добуток наступного вигляду:
((a, b), (c, d)) = ac + bd
При порівнянні (2.3) з (2.2) можна помітити наступне.
1. Результатом скалярного множення векторів є дійсне число, результатом множення комплексних чисел є комплексне число.
2. Дійсна частина скалярного множення комплексних чисел збігається зі скалярним множенням відповідних векторів, тобто, комплексне множення включає в себе векторне скалярне множення.
У лінійній алгебрі скалярний добуток дорівнює добутку довжин векторів на косинус кута між ними. Це означає, що два перпендикулярних вектора завжди будуть мати нульове скалярне множення, колінеарні ж вектора навпроти, будуть давати максимальне значення скалярного множення. Ці властивості множення дозволяють використовувати його як певну міру близькості векторів. Чим воно більше, тим менше кут між векторами, тим «ближче» вони один до одного. Для перпендикулярних векторів воно опускається до нуля, і далі стає негативним для векторів спрямованих у різні сторони. Скалярне множення (2.1) також володіє схожими властивостями.
Введемо поняття нормованого скалярного множення (НСП):
η = (Г, N)/|Г||N|
де: | Г | і | N | – норми (довжини) контурів, обчислювані як:
Г = (∑(k-1) n=0 |Yn 2)21/2
НСП в просторі комплексних чисел, також є комплексним числом. При цьому, одиниця – це максимально можливе значення модуля НСП (це випливає з нерівності Коші-Буняковського: | ab | ? | a | | b |), і вона досягається тільки якщо:
Г = µN
де: µ – випадкове комплексне число.
При множенні комплексних чисел, їх модулі (довжини) перемножуються, а аргументи (кути) складаються. Контур N є тим же контуром N, але повернений і промасштабірованний. Масштаб і поворот визначається комплексним числом. Модуль НСП досягає максимального значення одиниці, тільки якщо контур Г є тим же контуром N, але поверненим на деякий кут і про масштабувати на певний коефіцієнт [5].
3.4 Кореляційні функції контурів
НСП є корисною формулою для пошуку схожих між собою контурів. Але вибір початкової точки не дозволяє використовувати його безпосередньо. Рівність (2.6) досягається тільки якщо початкові точки контурів збігаються. Якщо контури однакові, але відлік ЕВ починається з іншого початкової точки, то модуль НСП таких контурів не повинна буде дорівнювати одиниці.
Введемо поняття взаімокорреляціонной функції (ВКФ) двох контурів:
(m) = (Г,N(m)), m = 0,…, k – 1
де: N (m) вибір початкової точки контур, отриманий з N шляхом циклічного зсуву його ЕВ на m елементів .
Для прикладу, якщо N = (n1, n2, n3, n4), то N (1) = (n2, n3, n4, n1), N (2) = (n3, n4, n1, n2) і так далі. Значення цієї функції показують наскільки схожі контури Г і N, якщо зрушити початкову точку N на m позицій. ВКФ визначена на всій множині цілих чисел, але оскільки циклічний зсув на k приводить нас до вихідного контуру, то ВКФ є періодичною, з періодом k. Таким чином будемо розглядати значення цієї функції тільки в межах від 0 до k-1.
Знайдемо величину, що має максимальний модуль серед значень ВКФ:
Ψmax = max(Ψ(m)/|Г||N|). m = 0, ....., k - 1
3.5 Автокорреляційна функція
З визначень НВВ і ВКФ, зрозуміло, що ?max є мірою схожості двох контурів, інваріантної переносу, масштабування, обертання і зрушенню початкової точки. При цьому, модуль |max| вказує ступінь схожості контурів, і досягає одиниці для однакових контурів, а аргумент arg (max) дає кут повороту одного контуру, щодо іншого.
Автокорреляційна функція є ВКФ для якої N = Г. По суті це скалярне множення контуру самого на себе при різних зрушеннях початкової точки:
v (m) = ( Г, Г(m) ), m = 0, … , k – 1
Розглянемо деякі властивості АКФ.
1. АКФ не залежить від вибору початкової точки контуру. Як бачимо, зміна початкової точки призведе просто до зміни порядку сумміруемих елементів і не призведе зміни суми (2.1).
2. Модуль АКФ симетричний щодо центрального відліку k/2. Оскільки АКФ є сумою попарних творів ЕВ контуру, то кожна пара зустрінеться два рази на інтервалі від 0 до k;
3. Розпишемо значення АКФ N = ( n1 , n2 , n3 , n4 ) для різних m:
АКФ(0)=(n1,n1)+(n2,n2)+(n3,n3)+(n4,n4)
АКФ(1)=(n1,n2)+(n2,n3)+(n3,n4)+(n4,n1)
АКФ(2)=(n1,n3)+(n2,n4)+(n3,n1)+(n4,n2)
АКФ(3)=(n1,n4)+(n2,n1)+(n3,n2)+(n4,n3)
АКФ(4)=(n1,n1)+(n2,n2)+(n3,n3)+(n4,n4)
Додатки в АКФ(1) ті ж самі, що і в АКФ (3), з точністю до перестановки множників. Для комплексних чисел (a,b) = (b,a)*, отримуємо що АКФ (1) = АКФ (3) * , де * - знак сполученого комплексного числа. Оскільки |a*| = |a|, то модулі АКФ (1) і АКФ (3) збігаються. Аналогічно, збігаються модулі АКФ (0) і АКФ (4). Далі будемо під АКФ розуміти тільки частину функції на інтервалі від 0 до k/2, оскільки інша частина функції симетрична першої частини. Якщо контур має будь-яку симетрію щодо повороту, то аналогічну симетрію має його АКФ. Для прикладу, наведемо графіки АКФ для деяких контурів. На рисунку 2.2 модуль АКФ зображений синім кольором (АКФ зображена тільки для інтервалу від 0 до k/2). Всі контури, крім останнього мають симетрію до повороту, що призводить до симетрії АКФ. Останній же контур такої симетрії не має, і графік його АКФ – не сіметричний.
АКФ контуру можна вважати характеристикою форми контура. Форми близькі до кола мають рівномірні значення модуля АКФ (див. рисунок 2 для кола). Сильно витягнуті в одному напрямку форми мають провал в центральній частині АКФ (див рисунок 2 для прямокутника). Форми, що переходять у самих себе при повороті, мають максимум АКФ у відповідному місці (див рисунок 2 для квадрата) [6-9].
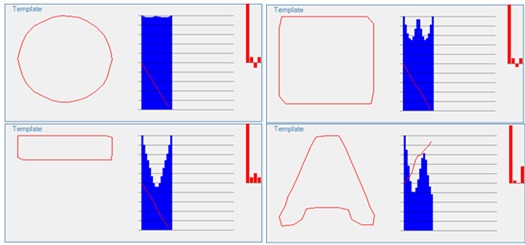
Рисунок 2 – Графіки контурів для деяких контурів
Нормована АКФ не залежить від масштабу, положення, обертання і вибору початкової точки контуру. Це випливає з пункту 1-го і з властивостей НВВ.
3.6 Загальний алгоритм розпізнавання
Загальна послідовність дій при розпізнаванні контурів на зображенні виглядає наступним чином:
1) попередня обробка зображення: згладжування, фільтрація перешкод, підвищення контрасту;
2) бінаризація зображення і виділення контурів об'єктів;
3) початкова фільтрація контурів по периметру, площі, коефіцієнту форми, фрактальности і так далі;
4) приведення контурів до єдиної довжині, згладжування;
5) перебір всіх знайдених контурів, пошук шаблону, максимально схожого на даний контур.
3.7 Оцінка продуктивності алгоритмів в контурному аналізі
Зробимо оцінку швидкодії алгоритмів, заснованих на контурному аналізі. Нехай зображення вже бінарізіровано і на ньому виділено контури. Оскільки надалі ми будемо працювати тільки з точками контурів, оцінимо загальна їх кількість на зображенні.
Розглянемо зображення розміром n*n пікселів. Покриємо його рівномірного сіткою з кроком s. Сумарна довжина всіх ліній сітки складе:
L = 2n2 /s
Перехід від плоского двовимірного зображення до контурів не применшує розмірність завдання.
Зауваження.
1. Наведена оцінка є екстремальною. У реальному зображенні не всі контури мають мінімальний розмір і вони не покривають всю площу зображення. Отже, число контурів і їх сумарний периметр може бути значно менше 2n2/s. В ідеальному випадку, якщо зображення містить один об'єкт, без перешкод, то КА буде працювати тільки з одним контуром, і число його пікселів складе вже не квадратичну, а лінійну залежність від n. У разі ж роботи із зображенням, як з двовимірним масивом пікселів (наприклад, застосовуючи каскадні фільтри Хаара) обробка виконується з усіма пікселами зображення, незалежно від того, скільки об'єктів на ньому зображено. Оскільки зображення у вигляді контурів вже має природну сегментацію та розбито на контури, то можна здійснювати фільтрацію частин зображення по простих ознаками, серед них: площа контуру, периметр, відношення квадрата периметра до площі (коефіцієнт форми). Таким чином, є досить простий і ефективний механізм попередньої фільтрації частин зображення.
2. Базові алгоритми двовимірних методів, як правило, не інваріантні до масштабу (SURF, SIFT) або обертанню (Хаар). Тому, фактично, вони працюють в тривимірному просторі, де ще один вимір з'являється через необхідність перебирати масштаби або кути повороту. Оскільки методи КА інваріантні до масштабу і обертанню, то такої проблеми не існує (виняток - неінваріантність до початкової точки).
3. Контурний аналіз дозволяє обробляти зображення в прогресивному режимі. Це означає, що можно впорядкувати контури за якою-небудь ознакою (наприклад, за площею чи за градієнтом кордонів, або по яскравості і т.п.). А потім обробити перший контур, і видати результат. Інші ж контури обробляти у фоновому режимі. Це означає що перший результат (а в багатьох прикладних задачах саме він і потрібний) може бути отриманий за O(n) , що є відмінною оцінкою для алгоритмів розпізнавання зображень;
4. Оскільки контури незалежні один від одного, то алгоритми розпізнавання легко распаралелювати. Крім того, алгоритми дуже прості і можуть виконуватися на графічних процесорах;
5. Все вищенаведене стосується тільки обробки контурів. Етап отримання самих контурів вимагає як мінімум O(n2). Однак, на практиці, цей етап займає не більше 10-20 % від загального часу обробки [10-12].Сукупність цих факторів істотно знижує константу обчислювальної складності, і при сучасному розвитку комп'ютерної техніки, КА цілком може використовуватися як алгоритм реального часу.
Cам контур, по суті, є одновимірним об'єктом. Це вектор комплекснозначних чисел. Однак число контурів зростає пропорційно квадрату розміру зображення. Найефективнішим засобом збільшення продуктивності є зменшення числа контурів попередньої фільтрацією. Оцінимо складність обробки окремо взятого контура. Скалярне множення вимагає O(k) операцій, де k – довжина контура. Для обчислення ВКФ потрібно провести k обчислень скалярних творів. ВКФ вимагає обчислень порядку O(k2 ). Враховуючи, що порівняння йде не з одним шаблоном, а з безліччю шаблонів, то повний час пошуку шаблону для контуру можна оцінити як:
O (k2t)
де: k – довжина контуру;
t – кількість шаблонних контурів.
3.8 Дескриптор контуру
Не дивлячись на те, що k – константа обчислення ВКФ є трудомістким процесом. При k = 30 на обчислення ВКФ потрібно 900 операцій множення комплексних чисел. За наявності t = 1000 шаблонів, пошук шаблону для контуру вимагає близько мільйона умножений комплексних чисел. Сам процес скалярного множення можна прискорити, шляхом стандартизації контуру і введення табличного множення. Але це не вирішує проблему кардинально. Витрати на стандартизацію теж великі і можуть перекрити гідності даного підходу.
Тому введемо більш ефективний спосіб пошуку та порівняння шаблонів. Для швидкого пошуку шаблонів необхідно ввести якийсь дескриптор, що характеризує форму контура. При цьому, близькі між собою контури повинні мати близькі дескриптори. Це позбавить від процедури обчислення ВКФ контуру з кожним шаблоном. Достатньо порівняти тільки дескриптори і, якщо вони будуть близькі, обчислювати ВКФ. Саме ж порівняння дескрипторів має бути швидким. В ідеалі дескриптором має бути одне число.
У першому розділі було розглянуто властивості автокореляційної функції та визначено що АКФ інваріантно до переносу, обертанню, масштабированию, вибору початкової точки і є функцією одного контуру (а не двох , як ВКФ). Виходячи з цього, АКФ можна вибрати в якості дескриптора, що описує форму контура. Близькі контури завжди будут мати близькі значення АКФ. Порівняння двох АКФ має складність O(k), що значно краще ніж O (k2) для ВКФ. Крім того АКФ через симетрії, визначено тільки на інтервалі від 0 до k/2, що ще в два рази зменшує складність обчислень.
Якщо база шаблонів зберігає їх АКФ, то пошук шаблону для контуру, шляхом порівняння АКФ, складе O(kt).
3.9 Згортка автокорреляційної функції
АКФ являє собою вектор з k/2 значеннями. Якщо обчислюти міру відмінностей двох АКФ, потрібно перебрати всі k/2 значень. Якщо поріг відмінностей фіксований, то можено на кожному кроці обчислювати поточну міру відмінностей, і як тільки вона перевищить поріг переривати порівняння АКФ . Таким чином можна прискорити порівняння АКФ . Однак є дві складності: по-перше, обчислення заходи на кожному кроці затратно за часом, по-друге, якщо відмінність відбувається в середині, або тільки в останніх компонентах значенні АКФ, то ефективність даного алгоритму падає, і він вироджується в повне порівняння. Для більш ефективного вирішення проблеми порівняння АКФ, змінимо спосіб представлення АКФ. Замість зберігання самої АКФ, будемо зберігати вейвлетного згортку модулів значень АКФ. При цьому перший компонент згортки відповідатиме найбільш великомасштабного вейвлет, а наступні компоненти будуть уточнювати значення функції у все більш дрібних масштабах. Вейвлетного згортка дозволить упорядкувати значення АКФ у масштабному порядку. Першим буде йти компонент, що відповідає найбільш великомасштабним особливостям АКФ, а подальші компоненти будуть уточнювати всі дрібніші особливості АКФ [13].
Вейвлетна згортка дає переваги при порівнянні АКФ. Порівнюючи перші компоненти згортки отримуємо порівняння АКФ в найбільш грубому наближенні. Якщо ці компоненти істотно відрізняються, подальші порівняння можна не робити, тому що АКФ гарантовано відрізняються. Далі, порівнюємо другий компоненти згортки, якщо вони істотно відрізняються також перериваємо порівняння і так далі. Крім того, можена не порівнювати всі k/2 компонент згортки. Оскільки порівняння носить оцінний, наближений характер, достатньо порівняти перші 4-5 значень згортки АКФ, потім при їх близькості відразу переходити до обчислення ВКФ. Відзначимо наступне.
1. Порівняння АКФ, в загальному випадку, не звільняє від необхідності обчислення ВКФ. Тільки ВКФ дає точну оцінку близькості контурів. АКФ в загальному випадку може збігатися для різних контурів. При цьому, попередній відбір шаблонів по АКФ істотно звужує число кандидатів на порівняння по ВКФ.
2. У ряді випадків, порівняння АКФ може бути достатньо для ідентифікації контурів. Якщо на зображенні шукаються маркери з простою геометричною формою і ймовірність помилкових распознаваний не істотна, то можна опустити процес порівняння ВКФ, обмежившись тільки порівнянням згорток АКФ. Такий алгоритм дає найбільшу продуктивність системи.
3. Перший компонент згортки АКФ дає хороший дескриптор для упорядкування бази шаблонів. Якщо для даного контуру підходять тільки шаблони, у яких перший компонент згортки приблизно дорівнює першому компоненту згортки контуру, то має сенс упорядкувати шаблони в базі по першому компоненту згортки. Це на порядок зменшує число шаблонів – кандидатів на порівняння. Для великих баз шаблонів це може дати хороший приріст продуктивності.
Розглянемо вибір конкретних вейвлетов для згортки. Можена використовувати будь згортки, у яких перший компонент характеризує функцію в найбільшому масштабі, а наступні уточнюють значення на більш дрібних масштабах.
Враховуючи що згортка потрібна для порівняння і АКФ часто є симетричною функцією, то не всі вейвлети однаково добре підходять для наших цілей. Основним критерієм до вибору вейвлета є його дискримінуючі властивості. Наприклад, розглянемо широко поширені вейвлети Хаара і Уолша (рис. 3).
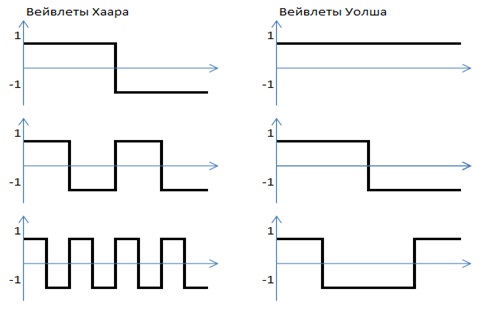
Рисунок 3 – Вейвлеты Хаара и Уолша
Через симетричності АКФ щодо центральної лінії , перший компонент вейвлета Хаара дасть нульове значення. Другий компонент вейвлета Хаара, також дасть нульове значення, через симетричності половинок АКФ щодо своїх середин. Крім того, перший компонент вейвлета Хаара дає нуль для всіх АКФ, крім останньої. Другий компонент Хаара також дасть нуль для контурів кола і квадрата. Однакові значення перших компонент говорить про погані дискримінують властивостях вейвлетов Хаара для згортки АКФ.
Перший компонент згортки Уолша є сумою всіх компонент АКФ. Ця сума різна для всіх прикладів АКФ. Це означає, що дискримінуючі властивості вейвлета Уолша для симетричних АКФ краще ніж вейвлета Хаара. Перші чотири компоненти згортки Уолша позначені червоними стовпцями. На рисунку 4 наведена гістограма частоти народження першого компонента згортки Уолша для бази шаблонів контурів латинських букв (всього в базі 3463 шаблону).
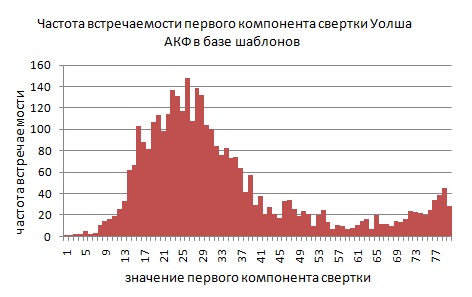
Рисунок 4 – Вейвлеты Хаара и Уолша
Дискримінуючий вейвлет повинен давати рівномірний розподіл для свого першого компонента. Згортка Уолша не дає рівномірного розподілу, однак її дискримінують властивостей першого компонента достатньо для зменшення простору пошуку шаблонів в три-чотири рази. Наприклад, перший компонент контуру зображення дорівнює 25 (одне з найбільш часто зустрічаються значень в базі шаблонів). Якщо прийняти порогову різницю згорток Lmax = 4, підійдуть шаблони в інтервалі від 21 до 29. З графіка видно, що в цьому інтервалі знаходиться близько 1000 шаблонів. Це становить 1000/3463 = 29% від усіх шаблонів. В найгіршому випадку, порівняння за перший компоненту згортки відфільтрує більше 70% невідповідних шаблонів.
В цілому, оптимальний вибір вейвлетів визначається характерними формами розпізнаваних об'єктів. Наприклад, якщо об'єкти симетричні, краще вибирати несиметричні базові функції вейвлетов.
3.10 Еквалізація контурів
У реальному зображенні контури мають довільну довжину. Тому, для пошуку та порівняння контурів, всі вони повинні бути приведені до єдиної довжині. Цей процес називається еквалізацією. У літературі описано спосіб еквалізациі, що дає на виході контур, що складається із заданого числа однакових за довжиною відрізків . Однак цей метод досить складний, так как потрібно буде проводити еквалізацію всіх контурів зображення, яких в загальному випадку О(n2).
Тому будемо застосовувати більш простий і швидкий спосіб еквалізациі, який крім приведення до єдиної довжині, робить згладжування контуру методом змінного середнього. Спочатку фіксується довжина ВК, яка буде використовуватися в системі розпізнавання. Позначимо її k. Для кожного вихідного контуру Г створюємо вектор - контур N довжиною k. Далі можливі два варіанти, або вихідний контур має більше число ЕВ ніж k, або менше число ніж k. Якщо вихідний контур більше необхідного, то перебираємо всі його ЕВ, і вважаємо елементи N як суму всіх ЕВ, наступним чином:
Complex[] newPoint = new Complex[newCount];
for (int i = 0; i < Count; i++)
newPoint[i * newCount / Count] += this[i];
Цей алгоритм досить грубий, особливо для довжин небагатьом великих k, однак він цілком застосовний на практиці. Якщо ж вихідний контур менше k, то виробляємо інтерполяцію, і вважаємо приблизно наступним чином:
Complex[] newPoint = new Complex[newCount];
for (int i = 0; i < newCount; i++)
{
double index = 1d * i * Count / newCount;
int j = (int)index; double k = index - j;
newPoint[i] = this[j] * (1 - k) + this[j + 1] * k; }
При малих значеннях k (менше 30) різко підвищується число шумових розпізнавань (розпізнавання як символів шуму чи інших несімвольних елементів зображення), знижується число вірних распознаваний, і збільшується число помилкових распознаваний. Таким чином, значення k = 30 є оптимальним для даної системи распознаваний.
Збільшення довжини контура, після певного рівня (25 і вище) не приводить до поліпшення якості розпізнавання. Це пов'язано з тим, що в описаному методі, еквалізация проводиться одночасно зі згладжуванням контурів. При великих значеннях довжини, згладжування стає все більш дрібномасштабним, і контур стає занадто деталізованим, і більш відмінним від шаблонних контурів [14].
Висновки
В результаті виконання даної роботи були розглянуті та проаналізовані наступні завдання:
1) розглянуті основні принципи побудови алгоритмів контурного аналізу, які дозволили розробити алгоритм;
2) обраний оптимальний алгоритм для написання програмного продукту, який максимально точно і за короткий час дає результат;
3) проведено огляд існуючих систем;
4) проаналізована оцінка продуктивності алгоритмів контурного аналізу, було виявлено, що при сучасному розвитку комп'ютерної техніки, контурний аналіз цілком може використовуваних як алгоритм реального часу;
5) у ході дослідження дескрипторів Фур'є з'ясувалося, що даний вид дескрипторів володіє всім вимогам до класифікації: инвариантность щодо повороту, масштабування і паралельного зсуву. У зв'язку з цим привид контуру до об'єкта амплітудному Фур'є спектру допомагає класифікувати даний об'єкт в режимі реального часу.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2015 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список викоритсаних джерел
- Фурман Я. А. Вступ в контурний аналіз. - М.: ФІЗМАТЛІТ, 2003. –561 с.
- Детектування автомобільних номерів на основі контурного аналізу [Електронний ресурс] – Режим доступа: http://mp3car.ru/blog/ComputerVision/15.html
- Цифрова обробка зображення/ Інтернет-ресурс. - Режим доступа: www / URL: http://rudocs.exdat.com/docs/index-87395.html - за голов. з экрану.
- Гонсалес Р. Цифрова обробка зображення в середовищі C # / Р. Гонсалес, Р. Вудс, С. Еддінс - М.: Техносфера, 2006. - 616с.
- Грібков І.В. Деякі питання кількісної оцінки продуктивності детекторів кордонів/ И.В. Грібков, А.В. Захаров, П.П. Кольцов и др. - М.: «Программні продукти і системи» № 4, 2011. - 234с.
- Леухін А.Н., Парсаев Н.В., Рахманов Х.Є. Алгоритм локалізації зображення реєстраційного номерного знаку автомобіля з використанням методів контурного аналізу [Електроний ресурс] – Режим доступа: http://hpc.marsu.ru/Content/articles/7.pdf
- Алиев М.В., Панеш А.Х., Каспарьян М.С. Виділення контурів на малоконтрастних і розмитих зображеннях за допомогою фрактальної фільтрації [Електронный ресурс] – Режим доступа: http://cyberleninka.ru/article/n/vydelenie-konturov-na-malokontrastnyh-i-razmytyh-izobrazheniyah-s-pomoschyu-fraktalnoy-filtratsii
- Костюкова Н.С., Коршун А.Н., Корольчук Е.А. Виділення контурів об'єктів в растрових зображеннях http://ea.donntu.ru:8080/jspui/bitstream/123456789/15503/1/163-170.pdf
- Потапов А.А., Гуляев Ю.В., Никитов С.А., Пахомов А.А., Герман В.А. Новітні методи обробки зображень - М .: ФІЗМАТЛІТ, 2008. –489 с.
- Гонсалес Р., Вудс Р.Цифрова обробка зображень Видавництво "Мир" Москва 1982 - 312 с.
- Анісімов Б.В., Курганов В.Д., Злобін В.Н. Розпізнавання і цифрова обробка зображень - М.: ФІЗМАТЛІТ, 2003. –561 с.
- Хуанг Т. Обробка зображень і цифрова фільтрація Переклад з анг. к.т.н. Е.З. Сорокін, В.А.Хлебородова Видавництво "Мир" Москва 1979 - 412 с.
- Форсайт Д. Комп'ютерне зір. Сучасний підхід. : Переклад з анг. - М.: Видавництво дом "Вільямс", 2004. - 928 с.
- OpenCV крок за кроком. Знаходження контурів і операції з ними [Електронный ресурс]. – Режим доступа: www/ URL: http://robocraft.ru/blog/compute rvision/640.html
