Дэвид Дэвидсон, ВЫЧИСЛИТЕЛЬНАЯ ЭЛЕКТРОМАГНИТНАЯ СИСТЕМА ДЛЯ радиочастотной И МИКРОВОЛНОВОЙ ТЕХНИКИ, стр. 29

 

Метод конечных разностей во временной области:

одномерное введение

2.1 Введение

Метод временной разностной временной области, обычно называемый FDTD (англ. аббривиатура), представляет собой конкретную реализацию общего класса методов, известных как методы с конечной разницей. Несмотря на то, что методы с конечной разницей охватывают широкий спектр сложности и точности, FDTD настолько широко используется в сообществе CEM, и именно FDTD почти всегда подразумевается в CEM (англ. Centre for Evaluation and Monitoring), когда упоминаются конечные различия.

Конечные разностные методы - это численные методы, в которых производные непосредственно аппроксимируются конечно-разностными факторами. Общий класс таких методов является наиболее интуитивным численным подходом и впервые был широко разработан научным компьютерным сообществом. По сей день он, наверное, остается наиболее универсально применимым численным методом и наиболее широко используемым для научных вычислений. Как уже говорилось, для динамических задач в CEM наиболее популярным является метод FDTD. В этой главе будут рассматриваться конечные различия в целом, прежде чем перейти к особенностям FDTD.

На этом этапе общее замечание о философии, лежащей в основе математической обработки вычислительных алгоритмов в этой книге, приемлемы. Хотя мы стараемся не быть «неаккуратным» математически, акцент в этой книге заключается в представлении известных методов для известных проблем в CEM, а не на основных математических требованиях к методам, как можно было бы ожидать, например, найдя в тексте прикладной математики. Примером данного вопроса, который мы будем рассматривать, по крайней мере на начальном этапе, является дифференциация разрывных функций, требующая обобщенной (слабой) производной, должным образом поля функционального анализа. К счастью, проблемы, основанные на физике, которые мы рассматриваем, обычно не свидетельствуют о том, какой тип патологического поведения может (справедливо сказать) относиться к математикам, а такие вопросы, как доказательства существования, обычно рассматриваются поверхностно, если вообще есть, в этой книге. Читателю следует предупредить о применении методов, обсуждаемых здесь, в других областях инженерной или прикладной науки, без дальнейшего более глубокого освоения основной теории.

 

2.2. Обзор конечных разностей

2.2.1. Основная процедура решения

Основные этапы любого метода конечных разностей можно резюмировать следующим образом.

• Разделите область решения на сетку узлов.

• Приближенные производные в данном дифференциальном уравнении с частными производными конечными разностями

с использованием значения решения в различных узлах.

• Решить разностные уравнения для значения решения на каждом узле с граничными и / или начальными условиями. При работе во временной области это означает поиск значений на следующем шаге. Этот процесс по-разному называют временной маршей, интеграцией времени или, в частности, в контексте FDTD, «прыгающей лягушкой».

Метод FDTD, являющийся подходом во временной области, является методом начальных значений (хотя, конечно, подразумеваются материальные границы). Конечно-разностные методы вообще могут работать как граничные значения, так и методы начальных значений.

2.2.2 Аппроксимация производных с использованием конечных разностей

Центральным для всех конечно-разностных методов является аппроксимация производных с конечными разностями. Из основного определения производной функции могут быть предложены различные численные аппроксимации. Однако, как правило, они производятся от расширения серии Тейлора, поскольку это обеспечивает ручку ошибки. В зависимости от того, задействованы ли «следующие», «предыдущие» или «центральные» узлы, можно получить следующее, обратное или центральное различие следующим образом:

Формула форвардной разницы для первой производной

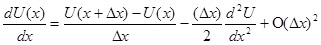                                                                                                        (2.1)                    

 

Формула обратной разности для первой производной

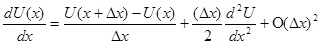                                                                                   (2.2)

 

Центральная разностная формула для первой производной

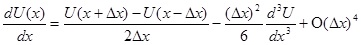                                                                       (2.3)

 

Эти выражения получены путем выполнения разложения по последовательностям Тейлора функции вокруг x. Рассмотрим вывод центральной разностной формулы. Разложение в ряд Тейлора вокруг x0, оцененное при x0+∆х, равно:

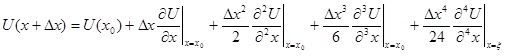                          (2.4)

 

 

 

ξ - точка, расположенная в интервале (x0, x0 +∆x). Это альтернативно можно записать в виде

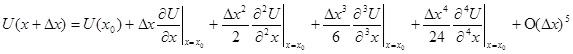       (2.5)

 

 

Аналогичное разложение выполняется относительно x0, оцененного при x0 -∆х:

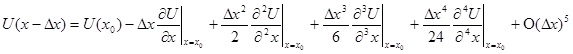       (2.6)

 

Вычитая два выражения, сгруппировав члены уравнения, разделив на ∆х и отметив, что остальные члены в ∆х сокращаются, получим уравнение (2.3).

Математическое определение - конечно-разностные аппроксимации второй производной

Если вместо разностных уравнений (2.5) и (2.6), как и выше, добавим их, получим формулу для центральной разностной аппроксимации второй производной функции. Результат с остаточным членом второго порядка:

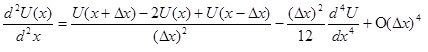                                                   (2.7)

 

(Заметим, что члены в (∆х)³ также сокращаются.) В FDTD мы не будем напрямую использовать эту формулу, но оказывается, что схема FDTD также является точной по второму порядку. Причина в том, что центральная разностная формула для второй производной также может быть получена путем объединения выражений для форвардных и обратных производных в первый порядок, что и делает FDTD.

Хотя уравнения (2.1), (2.2) и (2.3) кажутся одинаковыми - действительно, первая часть каждой из них идентична - остальные члены (ошибки) не являются. Как для прямого, так и для обратного разнесения ошибка пропорциональна длине ячейки (∆ X) (также известной как схема первого порядка), но для центрального разнесения она пропорциональна ее квадрату или, альтернативно, схеме второго порядка. Ясно, что в пределе ∆x → 0 центральная разностная формула будет сходиться быстрее к истинному значению производной.

Эта идея прямой дискретизации производных лежит в основе метода FD; следует рассмотреть это как класс методов, поскольку существует множество вариантов, которые можно сделать в отношении конкретного алгоритма FD. Прежде чем перейти к методу FDTD, необходимо сделать последнюю общую точку: методы FD могут быть либо неявными, либо явными. Это особенно актуально, когда время является одной из переменных. Неявный метод требует решения набора одновременных уравнений - матричного уравнения - для оценки неизвестных. Полученная матрица, как правило, очень разрежена, то есть имеет только несколько ненулевых записей. Эффективные решатели FD используют это, чтобы сохранить как память, так и вычислительное время.) С точки зрения физики с явным методом «следующее» значение в точке является функцией не только текущих и прошлых значений в этой и соседних точках, но и «следующие» значения некоторых или всех этих. В явном методе каждое неизвестное может быть получено непосредственно в терминах заданных или ранее вычисленных значений. Физически следующее значение вычисляется полностью из текущих или прошлых значений. Явные методы не требуют никакого матричного решения. Тем не менее, они обычно имеют некоторый максимальный размер временного шага, который, если превышен, вызывает нестабильность (обычно известную как предел Куранта).

Следует отметить, что существуют другие методы получения числовых производных. Используя больше точек, можно получить схемы более высокого порядка. Тем не менее, схема Yee (алгоритм Йи), которая будет обсуждаться, в целом не подходит для них.