Горяйнова Анастасія В'ячеславівна
Системи штучного інтелекту
Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Мета і задачі дослідження та заплановані результати
- 2. Актуальність теми
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд національних джерел
- 3.3 Огляд локальних джерел
- 4. Постановка завдання та отримані результати
- Висновки
- Перелік посилань
Вступ
Кінцевий автомат (state machine) – модель, яку зручно використовувати в самих різних областях, починаючи від моделювання логічних пристроїв в технічній діагностиці та закінчуючи структуруванням додатків. Зокрема, одним з додатків кінцевих автоматів є моделювання несправностей дискретних пристроїв. Часто такі несправності можна описати, як перекидання дуг в автоматі при збереженні вихідних реакцій.
Представляють інтерес такі перекидання, які не змінюють поведінки автомата. Відомий ряд робіт, в яких досліджуються властивості перекидань такого роду. У даній роботі триває дослідження властивостей автоматів, схильних до перекидання дуг за умови, що автомат груповий і не змінює своєї поведінки під дією перекидання.
Будемо говорити, що автомат допускає перекидання, якщо в результаті неї виходить автомат, ізоморфний вихідного. Таку перекидання будемо називати допустимої, а допустиму перекидання k-дуг, будемо називати k-перекиданням.
1. Цілі, завдання і плановані результати
Об'єктом дослідження є поведінка кінцевого наведеного групового автомата при перекиданні дуг.
Предметом дослідження є виявлення умов, при яких, автомат допускає перекидання k-дуг, зберігаючи при цьому ізоморфізм і властивість бути груповим.
Метою магістерської дисертації є розробка і дослідження методу аналізу групових автоматів і допустимих ними перекидань дуг.
Основні завдання роботи:
- провести аналіз поведінки групового автомата в результаті перекидання k-дуг, де k ≥ 1;
- з'ясувати існування допустимих k-перекидань і описати структуру автоматів, які допускають їх;
- розробити алгоритм побудови допустимих k-перекидань;
2. Актуальність теми
Модель кінцевого автомата пройшла хорошу перевірку часом. Використання кінцевих автоматів дозволяє розробникам створювати добре організовані логічні системи з гнучкими можливостями, а також аналізувати їх поведінку в різних умовах.
Наприклад, в іграх часто використовують різні персонажі, які переміщаються в області гри і можуть діяти в різних режимах. Використання кінцевих автоматів з чітко визначеними правилами для кожного персонажа, визначальними можливі варіанти його поведінки в різних станах і допустимі переходи з одного стану в інший, дозволяє створювати складні варіанти поведінки як персонажів, керованих комп'ютером, так і персонажів, керованих користувачем [1].
Справжня робота відноситься до теорії експериментів з автоматами. Експериментом називають процес подачі на автомат послідовності вхідних сигналів, спостереження відповідної реакції автомата і висновок укладення про функціонування і властивості автомата, заснованих на цих спостереженнях і апріорної інформації про автомат. Основне завдання теорії експериментів полягає в розробці ефективних експериментів, що дозволяють отримати певні відомості про будову автомата, його функціях, про характеристики процесу перетворення інформації, здійснюваного цим автоматом.
Таким чином, дослідження моделі кінцевого автомата і вивчення його поведінки є актуальним завданням.
3. Огляд досліджень та розробок
3.1 Огляд міжнародних джерел
Автомати, близькі по поведінці в тому чи іншому сенсі, досліджуються досить давно, так само, як і структура класів таких автоматів. В основному, це завдання розглядається в рамках теорії експериментів з автоматами.
Підстава теорії експериментів з автоматами було покладено Муром [2]. У його роботах дослідження проводилося в двох напрямках: не можна відрізнити автоматів ніяким кратним і ніяким простим експериментом, а також розпізнавання автомата і його станів за допомогою таких експериментів. Надалі теорія експериментів отримала розвиток в роботах Ф. Хенні, Милі, Брауера і інших[3-6]. Методи і результати аналізу автоматів і алгоритмів проведення експериментів з ними досить повно представлені у відомій книзі А. Гілла [7].
3.2 Огляд національних джерел
Вітчизняні роботи в області експериментів з автоматами пов'язані з іменами A.M. Богомолова та його учнів, М.П. Василевського, В.Н. Носкова, Н.В. Євтушенко, А.Ф. Петренко, І.К. Рисцова, В. А. Твердохлебова, С.В. Яблонського, В.Б.Кудрявцева і ін. [8-16].
Теорія експериментів інтенсивно розвивається і в даний час. [17-18] отримано ряд результатів, пов'язаних з аналізом поведінки автоматів в умовах впливу на них факторів зовнішнього середовища. У ряді робіт вивчався вплив перекидань дуг на поведінку автомата. В теорії графів також розглядалися родинні завдання, де вивчалася задача визначення, коли один з графів (автомат) може бути отриманий з іншого в результаті деякої послідовності перекидань дуг [19].
3.3 Огляд локальних джерел
У донецькому національному технічному університеті (кафедра системного аналізу і штучного інтелекту) поведінка автомата, схильного повітряні перевезення дуг, досліджувався в роботах Копитова О. М, Бурлаевой Е. І., Швець О.А. і ін. В [20-24] отримані наступні основні результати:
- перекидання однієї дуги в наведеному автоматі Мілі завжди призводить до неізоморфних автоматів;
- перекидання двох дуг може породжувати автомат, еквівалентний вихідному;
- для будь-якого натурального k > 1 існує наведений автомат, в якому знайдеться підмножина з k дуг, одночасна перекидання яких призводить до ізоморфного автомату;
- при перекиданні двох дуг вхід-вихідні позначки на перекинутих дугах повинні збігатися;
- можливі перекидання більше двох дуг, при яких вхід-вихідні позначки на перекинутих дугах різні;
- отримано ряд необхідних і достатніх умов, при яких перекидання двох дуг зберігає ізоморфізм вихідного і перетвореного автоматів;
- представлена структура автоматів, в яких можлива перекидання будь-якого числа дуг ≥ 2, причому ці автомати не є сильно зв'язковими;
- показано, що перекидання дуг, яка зберігає ізоморфізм, можлива в автоматах, що володіють певною симетрією графа переходів, від якої потерпають і в циклічній структурі графа;
- існують приклади сильно зв'язкових автоматів, в яких існує ≥ 3–х перекидань, що зберігають ізоморфізм.
Як бачимо, для довільного наведеного автомата поки не отримано критерій збереження ізоморфізму при перекидання дуг. У даній роботі досліджується окремий випадок перекидань, а саме, перекидання в групових автоматах.
4. Постановка завдання та отримані результати
Автомат називається груповим, якщо в ньому перехід по кожному вхідному символу задає деяку перестановку на безлічі станів. Як відомо, безліч перестановок n елементів з операцією композиції на ньому є групою.
Під автоматом будемо розуміти наведений автомат Мілі (S, Х, Y, δ, λ), де S, Х, Y – множини станів, вхідних і вихідних символів відповідно, а δ, λ – функції переходів і виходів, причому ∀ x: { δ(s, x) | s ∈ S} = S.
Нагадаємо визначення наведеного автомата. Два стану s і t одного і того ж автомата A або двох різних автоматів A і B відповідно, називаються еквівалентними якщо для будь-якого вхідного слова р∈X* виконується λ(a,p)=λ′(b,p), где λ ′ – функція виходів автомата A або B. Автомат називається наведеним, якщо всі його стану попарно нееквівалентний. Кожному стану s поставимо у відповідність безліч λs всіх вхід-вихідних слів, породжуваних цим станом.
Автомат в нашому випадку зручно задавати у вигляді графа переходів, вершини якого відповідають станам з S, а дугами є четвірки (s,x,y,t), де t = δ(s,x), y = λ(s, x). Пара (x,y) називається відміткою дуги, s - її початком, а t - кінцем. Якщо e = (t, x, y, u) - дуга в графі переходів автомата A, то перекиданням цієї дуги зі стану u в стан v, відмінне від u, називаємо заміну її дугою (t, x, y, v).
Вплив перекидань дуг на поведінку автомата будемо вивчати в таким чином:
- спочатку розглянемо перекидання рівно однієї дуги;
- потім сформулюємо результати стосуються перекидання рівно 2-х дуг;
- після цього перейдемо до вивчення перекидання k-дуг, де k > 2;
До теперішнього часу отримані наступні результати:
Теорема 1. Перекидання однієї дуги в груповому автоматі завжди призводить до неізоморфних автомату.
Дійсно перекидання дуги (sk, x, y, sk+1) в стан sj ≠ sk+1 призводить до того, що стан sk+1 перестає бути наступником будь-якого стану по вхідному символу x, тобто автомат перестає бути груповим.
Теорема 2. Перекидання двох дуг в груповому автоматі завжди призводить до неізоморфних автомату.
Доказ озаснований на тому очевидному факті, що у ізоморфних автоматів для будь-якого вхідного символу існує однакове число циклів.
Покажемо, що в результаті перекидання двох дуг це властивість порушується.
Нехай дуга (sk, x, yk, sk+1) перекидається в стан sj ≠ sk+1, т.е. тобто замінюється дугою (sk, x, yk, sj). Можливі два випадки: 1) sj належить тому ж циклу, що sk+1 і 2) sj пналежить іншому циклу. Нехай до перекидання стан sk належить деякому циклу по x:
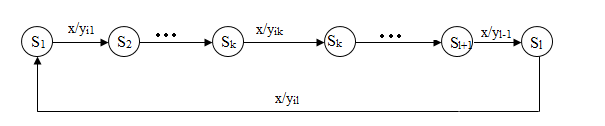
Малюнок 1 – Цикл по x довжини ≤ l
Розглянемо перший випадок, який наочно показаний на малюнку 2.
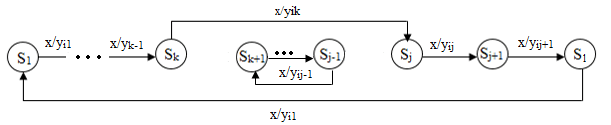
Малюнок 2 – Перекидання двох дуг в циклі по xi довжини n
З малюнка видно, що для збереження автоматом властивості бути груповим
в ньому необхідно перекинути дугу (sj-1, x, yij-1, sj)
в стан sk+1, тобто замінити її дугою
(sj-1, x, yij-1, sk+1).
ННеважко бачити, що в результаті таких двох перекидань один цикл по
х (показаний на малюнку 1) замінюється двома циклами
(показаними на малюнку 2), тобто кількість циклів по х збільшується.
Розглянемо другий випадок, коли стану sk+1 і sj принадлежат разным циклам – належать різним циклам - як показано на малюнку 3.
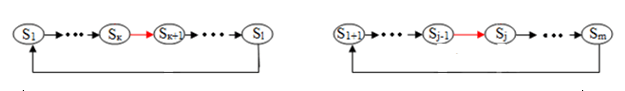
Малюнок 3 – Два циклу по x
Після перекидання дуги (sk, x, yk, sk+1) в стан sj
для збереження автоматом властивості бути груповим
в ньому необхідно перекинути дугу
(sj-1, x, yj-1, sj) в стан sk+1, тобто замінити її дугою
(sj-1, x, yj-1, sk+1).
Неважко бачити, що в результаті перекидання дуг замість двох
циклів по x отримуємо один цикл (показаний на малюнку 4).
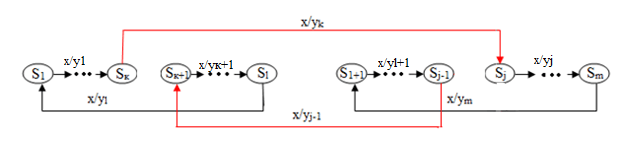
Малюнок 4 – Перекидання двох дуг між циклами
Зміна числа циклів по х в обох випадках доводить теорему.
Теорема 3. Для будь-якого до к ≥ 3 існує груповий автомат, що допускає перекидання k-дуг.
Доведення. Побудуємо груповий автомат з числом станів k ≥ 3, двома вхідними і двома вихідними символами {0,1}. За 0 автомат містить один цикл, причому їхні стани з першого по (k-1)-й видають реакцію 0, а k-тий стан видає реакцію 1. За 1 для всіх станів є петля з вихідним символом 0 (показано на малюнку 5) .
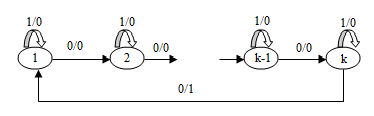
Малюнок 5 – Загальний вигляд групового автомата
Легко бачити, що автомат наведений і груповий. Виконаємо такі перекидання: змінимо напрямок всіх дуг по 0 на зворотне (показано на малюнку 6).
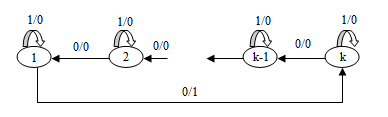
Малюнок 6 – Груповий автомат після перекидання k-дуг
Ясно, що в результаті перекидання отримуємо автомат ізоморфний вихідного.
Наведемо приклад перекидання чотирьох дуг.
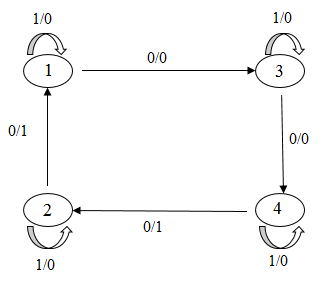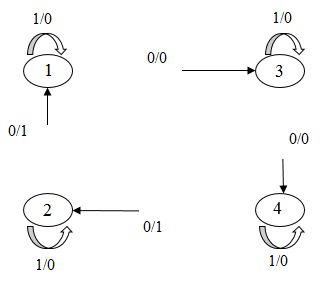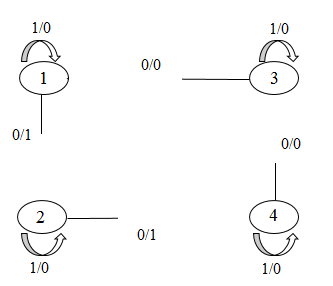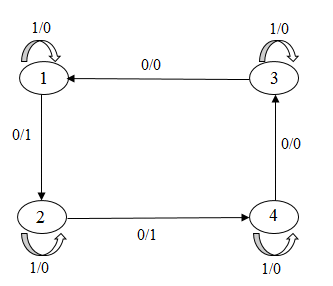
Рисунок 7 – Перекидання 4-х дуг у групповому автоматі
(анімація:
17 кадрів, 3 цикла повторювання, 82,1 кілобайт)
Висновки
До теперішнього часу отримані наступні результати:
- доведено, що перекидання однієї і двох дуг завжди призводить до неізоморфних автоматів;
- доведено, що для будь-якого к ≥ 3 існує груповий автомат, що допускає перекидання k-дуг;
- наведено приклад перекидання чотирьох дуг зі збереженням ізоморфізму;
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: червень 2017 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список джерел
- Салмре И. Программирование мобильных устройств на платформе .NET Compact Framework / И. Салмре. – М.: Вильямс, 2006. – 702 с.
- Мур Э.Ф. Умозрительные эксперименты с последовательностными машинами / Э.Ф. Мур // Автоматы. – М.: Иностранная литература, 1956. – С. 179-210.
- Hennie F. C. Fault detecting experiments for sequential circuits / F. C. Hennie // Proc. 5 Annual Symp. Switch. Circuits Th. and Logic. Design. – 1964. – P. 95-110.
- Bhattacharyya A. Checking experiments on sequential machines / A. Bhattacharyya. – New York: J. Wiley and Sons, 1989. – 155 p.
- Kohavi Z. Switching and finite automata theory / Z. Kohavi. – New York: Mc Graw Hill, 1970. – 522 p.
- Брауэр Р. Введение в теорию конечных автоматов / Р. Брауэр. – М.: Радио и связь, 1987. – 392 с.
- Гилл А. Введение в теорию конечных автоматов / А. Гилл. – М.: Наука, 1966. – 272 с.
- Богомолов А.М., Барашко А.С., Грунский И.С. Эксперименты с автоматами / А.М. Богомолов, А.С. Барашко, И.С. Грунский. – Киев: Наукова думка, 1973. – 144 с.
- Богомолов А.М., Грунский И.С., Сперанский Д.В. Контроль и преобразования дискретных автоматов / А.М. Богомолов, И.С. Грунский, Д.В. Сперанский. – Киев: Наукова думка, 1975. – 176 с.
- Богомолов А.М., Салий В.Н. Алгебраические основы теории дискретных систем / А.М. Богомолов, В.Н. Салий. – М.: Наука, 1997. – 386 с.
- Евтушенко Н.В., Матросова А.Ю. К синтезу контролепригодных автоматных сетей / Н.В. Евтушенко, А.Ю. Матросова // Техническая диагностика. – 1991. № 3. – С. 143-152.
- Евтушенко Н.В., Петренко А.Ф. Метод построения проверяющих экспериментов для произвольного недетерминированного автомата / Н.В. Евтушенко, А.Ф. Петренко // Автоматика и вычислительная техника. – 1990. № 5. – С. 73-76.
- Евтушенко Н.В., Петренко А.Ф. О проверяющих возможностях кратных экспериментов / Н.В. Евтушенко, А.Ф. Петренко // Автоматика и вычислительная техника. – 1989. № 3. – С. 9-14.
- Петренко А.Ф. Эксперименты над протокольными объектами / А.Ф. Петренко // Автоматика и вычислительная техника. – 1987. № 1. – С. 16-21.
- Petrenko A.F., Yevtushenko N., Dsouli R. Grey box finite state machine base testing strategies / A.F. Petrenko, N. Yevtushenko, R. Dsouli // Depart d’informatique et recherch. operat. Univ de Moutreal, 1994. Publ 991. – 22 p.
- Грунский И.С., Копытова О.М. О структуре контрольного эксперимента для определенно-диагностируемого автомата / И.С. Грунский, О.М. Копытова // Теория управляющих систем. – К.: Наук.думка, 1987. – С. 40-54.
- Грунский И.С., Копытова О.М. Неотличимость конечных автоматов в стационарной среде наблюдения / И.С. Грунский, О.М. Копытова // Дискретная математика. – 1993. – Т.5, вып.4. – С. 43-53.
- Копытова О.М. Неотличимость конечных автоматов кратными экспериментами в стационарной среде наблюдения / О.М. Копытова // Дискретная математика. – 1994. – Т.6, вып.2. – С. 120-128.
- Козловский В.А. О классе графов, порожденных локальными преобразованиями заданного графа / В.А. Козловский // Методы и системы технической диагностики. – Саратов: Изд-во Саратов. Ун-та. – 1985. – Вып.5. – С. 65-70.
- Копытова О.М. О структуре автоматов, сохраняющих
поведение при перебросках дуг / О.М. Копытова // Труды VIII Международной конференции
Дискретные модели в теории управляющих систем
(20.04 – 22.04.2015). Москва: Макс-Пресс, 2009. – С. 155-159. - Копытова О.М. Устойчивость автоматов к неисправностям их функции переходов / О.М. Копытова // Тр. ин-та ИПММ АН Украины. – 2010. – № 21. – С. 57-66.
- Бурлаева Е.И., Копытова О.М. Об одном типе локальных
преобразований автомата / Е.И. Бурлаева, О.М. Копытова // Материалы IV всеукраинской научно-технической
конфиренции студентов, аспирантов и молодых ученых
Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2013)
(24.04 – 25.04.2013). Донецк: ДонНТУ, 2013. – С. 479-484. - Копытова О.М. О возможности сохранения поведения автомата
при перебросках дуг / О.М. Копытова // Материалы VI Международной научно-практической конференции
Новости научной мысли – 2010
(27.10 – 05.11.2010), Чехия. Прага. Издательский домОбразование и наука
, 2010. – С. 41-46. - Швец О.С., Копытова О.М. О сравнении поведения ОДk-эталона
и автоматов, порождаемых его локальными преобразованиями / О.С. Швец, О.М. Копытова // Материалы
V всеукраинской научно-технической конференции студентов, аспирантов и молодых
ученых
Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2014)
(22.04 – 23.04.2014). Донецк: ДонНТУ, 2014. – С. 365-369.
