Обратимые конечные автоматы и условия вложения полугруппы в группу
Автор: Н.И. Крайнюков
Источник: Вектор науки ТГУ. № 3(13), 2010 УДК 004.421:004.912 управление, вычислительная техника и информатика
Н.И. Крайнюков, кандидат технических наук, доцент кафедры
Прикладная математика и информатика
Тольяттинский
государственный университет, Тольятти (Россия).
Ключевые слова: обратимые и бидетерминированные автоматы; полугруппа; действия полугруппы на конечных множествах состояний; синтаксический моноид; свободная группа.
Анотация: в статье рассматриваются вопросы представления регулярных языков в виде разложения на входящий язык, язык внутреннего цикла и выходящий язык по состояниям конечного автомата. Для класса обратимых и бидетерминированных автоматов, такое разложение обладает рядом свойств, для исследования которых применяются алгебраические методы.
Введение
Конечные автоматы и регулярные языки позволяют привести примеры действия полугруппы на конечных множествах состояний, исследовать регулярные выражения и алгоритмы поиска слов языка в произвольном массиве данных [1,2]. В статье обсуждаются вопросы, которые расположены в пересечении нескольких предметных областей: алгебры, информатики и практического программирования. Практические задачи быстрого поиска, задачи построения минимальных конечных автоматов и другие задачи, связанные с дискретной оптимизацией сложных проблем высокой размерности, требуют разработки новых эвристических алгоритмов [3].
Прведварительные сведения
Пусть X – конечный алфавит, X* – свободный моноид над алфавитом X={x1, x2,…xn}. Регулярный язык L является множеством классов эквивалентности гомоморфизма f(X*) из свободного моноида X* в конечный синтаксический моноид M=M(L), порожденный синтаксической конгруэнцией множества L.
Регулярный язык L может быть задан конечным автоматом A = (Q, X, δ, I, F) ), где Q – конечное множество состояний, X – входной алфавит, δ – функция переходов состояний, под действием символов входного алфавита X, δ:Q×X→2Q, I – множество начальных состояний, F – множество заключительных состояний, 2Q – множество всех подмножеств пространства состояний автомата A.
Предполагается, что автомат считывает входное слово слева направо и переходит из начального состояния, согласно функции переходов. Функцию переходов δ(q,x) расширяют на X* стандартным способом ˆδ : Q×X*→2Q.
Слово w распознается (допускается) автоматом, если ˆδ(q,w)∈F.
Конечный автомат A является детерминированным (ДКА), если он имеет не более одного начального состояния и |δ(q,a)|≤1 и для любых q и a; в противном случае он называется недетерминированным (НКА). Автоматы представляются: в виде таблицы функции переходов, графов состояний и дерева автомата [4].
Слово языка обычно считывается слева направо, но в некоторых языках чтение производится справа налево. Определение зеркального автомата и зеркального языка приведено в [3], для двойственных объектов движение обратное, справа налево.
Слово языка обычно считывается слева направо, но в некоторых языках чтение производится справа налево. Определение зеркального автомата и зеркального языка приведено в [3], для двойственных объектов движение обратное, справа налево.
Зеркальный язык языка L, обозначение LR – это множество слов языка L взятых в обратном порядке. Пример: если слово abb принадлежит языку L, то слово bba принадлежит языку (LR)R. Сопоставление языку L зеркального языка является инволюцией: (LR)R = L.
Зеркальный автомат AR, обозначение AR = (Q, X, δR, F,I), это автомат, в графе состояний которого направление стрелок, помеченных буквами входного алфавита, изменено на обратное, а входящие состояния заменены на допускающие, а допускающие на входящие состояния. Соответствующим образом определяется функция переходов δR. Сопоставление автомату его зеркального является инволюций.
Слово w= x1, x2,…xn распознается (принимается) автоматом A, если существует путь по ребрам графа автомата A c началом пути – во множестве начальных состояний I, и конечным состоянием – во множестве заключительных состояний F.
Язык LR распознаваемый зеркальным автоматом AR, является зеркальным к исходному языку L.
Разложение регулярного языка по состояниям
Удобно разделить, допустимые слова языка Z, проходящие через состояние q на три части, фактически на три языка: Lq(Z) – входящий (левый) язык состояния q, Cq(Z) – язык внутреннего цикла состояния q, Rq(Z) – выходящий (правый) язык состояния q. Понятно, такие языки для любого состояния q, будут регулярными и соединение соответствующих слов, этих языков по всем состояниям даст исходный язык Z. Для зеркального языка ZR движение по состояниям происходит в обратном порядке, и входящий язык Lq(ZR) становится правым Rq(Z) для языка Z, слова языка внутреннего цикла Cq(ZR) – проходятся в обратном направлении по отношению к словам языка Cq(Z); аналогично для выходящего языка Rq(ZR). Таким образом, двойственность или зеркальность сохраняется и для входящего языка, выходящего языка и языка внутреннего цикла.
Для более подробного рассмотрения взаимосвязи между этими тремя языками и состояниями автомата определим тернарное отношение K(w,q,v)=1,если wv ∈ Z и ˆδ(I,w)⊃q иˆδR(F,vR) и K(w,q,v)=0 , в противном случае. Отношение K(w,q,v) определяет представление языка Z в виде разложение входящего языка Lq(Z) и выходящего языка Rq(Z).
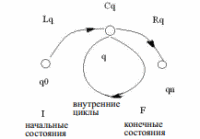
Рис. 1. Разделение допустимого слова, проходящего через состояние q, на три части – Lq, Cq, Rq.
Введем лексикографическое упорядочение в алфавите X={x1 < x2 <,...xn} и соответствующим образом упорядочим слова в свободном моноиде X*.
Построим отношение K(w,q,v), тогда, проекция на плоскость (w,v) – даст MZ(w,v) – матрицу представления языка Z. Ненулевые элементы MZ(w,v) представляют разложение слов языка Z в виде произведения подслов w и v.
Теорема 1. Пусть Z=L(A) – язык распознаваемый недетерминированным автоматом A, который имеет n – состояний q1,...qn и слово z=wv∈Z и ˆδ(I,w)⊃q1. Для зеркального языка ZR R и зеркального автомата ARˆδR(F,vR)⊃q1.
Обозначим таблицу S(w,qi)=1, если ˆδR(I,w)⊃q1. S(w,qi )=0 в противном случае. Назовем матрицу S(w,qi) – матрицей состояний на подсловах языка Z. Матрица S(w,qi ) имеет размерность (∞,n). Аналогичная матрица SR (q1,vR) имеет размерность (n,∞). Тогда MZ(w,v) – матрица представления языка Z допускает разложение MZ≈S×SR. Соответствие ≈ означает, что расположение нулевых элементов матриц совпадают (слово языка не проходит через состояние), и не нулевые элементы (слово языка проходит через состояние) тоже совпадают.
Доказательство: так как z=wv ∈ Z и ˆδ(I,w)∩ˆδR(F,vR)⊃q1, значит произведение S×SR(w,vR)≠0. Поэтому MZ (w,v) матрица представления языка Z допускает такое разложение. Для бидетерминированного автомата, в виду единственного пути для слова допускаемого прямым автоматом и его зеркальным автоматом разложение ≈, заменяется обычным равенством.
Бидетерминированные и обратимые автоматы
Автомат A называется бидетерминированным (кодетерминированным), если зеркальный автомат AR, является детерминированным. Понятно, что в этом случае автомат A должен иметь одно заключительное состояние.
Для обратимых и бидетерминированных автоматов матрица представления языка будет равна произведению матриц состояний для прямого и зеркального автомата.
Предположим, что каждый символ входного алфавита X является частичным взаимнооднозначным отображением множества состояний Q автомата A в себя – в этом случае автомат A называется обратимым или инъективным. В отличие от бидетерминированного, автомат A может иметь несколько входных и/или выходных состояний. Обратимые автоматы могут быть как детерминированными, так и недетерминированными. Автомат A – называется групповым, если действие любого входного символа является взаимнооднозначным отображением на все множество состояний Q.
Класс языков, определяемый бидетерминированными автоматами, не замкнут относительно объединения. Подавтомат (определение подавтомата в [4]) обратимого и бидетерминированного автомата является обратимым и бидетерминированным соответственно.
Класс языков, определяемый обратимыми автоматами, замкнут относительно объединения. В качестве автомата, распознающего объединении языков, можно взять непересекающееся объединение соответствующих автоматов.
Обратимые автоматы с совпадающим начальным и конечным состояниями связаны с конечнопорожденными подгруппами свободной группы. Рассмотрим граф переходов такого бидетерминированного автомата с другой стороны, а именно как 1–мерный комплекс с помеченными ребрами [7]. Согласно [7; теорема 2.1], любой конечный связанный 1–мерный комплекс гомотопически эквивалентен букету окружностей. Пути по графу состояний, начинающиеся и заканчивающиеся в одной точке, можно проходить последовательно (ассоциативность произведения путей). Обратный элемент – путь в обратном направлении, он существует и единственен, поскольку автомат A обратим. Множество путей образует группу. Это фундаментальная группа 1–мерного комплекса. Согласно [7; теорема 2.8], фундаментальная группа букета n окружностей изоморфна свободной группе с n образующими.
Выделенное направление (стрелочка на ребре графа и буква) соответствует введению ориентации на 1–мерном комплексе. Для того чтобы задать противоположную ориентацию, дополним исходный алфавит X соответствующими буквами с чертой, имеющими смысл обратных для букв алфавита X и обозначим ¯X, и X∪{¯x1,¯x2,…¯xn} – свободный моноид. Свободная группа FG(X), задается определяющими соотношениями R= < x1⋅¯x1=1,¯xn⋅x1=1,…xn⋅¯xn=1,¯xn⋅xn=1.
Определим подмножество L свободной группы FG(¯X), которое распознается автоматом A. Дополним граф автомата A ребрами, помеченными буквами, так, чтобы «прямое» ребро, помеченное буквой xi, соответствовало «обратному ребру», помеченному буквой c чертой xi, и обозначим полученный автомат ¯A=(Q,¯X, ¯δ, I, F).
Слово w, принадлежащее свободной полугруппе ¯X∗, и, соответственно, свободной группе FG(¯X), определяет путь на графе автомата A, соответствующий слову w. Рассмотрим отображение π:¯X∗→FG(¯X). Исходный автомат A будет расознавать язык L(A), равный пересечению свободного моноида X∗ и языка L(¯A).
Граф автомата является графом образующих конечнопорожденной подгруппы в свободной группе FG(¯X).
Согласно [6; теорема 3.2], подмножество L свободной группы FG(¯X) принимается обратимым автоматом A тогда и только тогда когда L является конечным объединением левых смежных классов конечно порожденной подгруппы свободной группы.
Пример 1. Рассмотрим автомат A1, заданный таблицей состояний (рисунок 2).
Граф автомата A1 можно преобразовать (упростить) без потери путей объединяя состояния 4, 2, 7 в одно состояние, а затем объединяя новое полученное состояние с состоянием 3. Результат преобразования автомата A1 представлен на рис. 3 в виде графа состояний автомата A2.
Регулярное выражение (aaUaabbUaba)* определяет язык недетерминированного автомата A1, а регулярное выражение (bbUab*a)* – язык детерминированного автомата A2. Языки, определяемые этими выражениями, различны, но все пути/циклы автомата A1 находятся среди путей/циклов автомата A2. Таким образом, детерминированный автомат A2 имеет меньшее число состояний, и язык L(A2) включает язык L(A1). Такой алгоритм сворачивания ребер графа состояний эквивалентен выделению системы образующих подгруппы в конечнопорожденной свободной группе и может использоваться в качестве вспомогательного, эвристического алгоритма для поиска недетерминированных автоматов, эквивалентных заданному и имеющих минимальное число состояний.
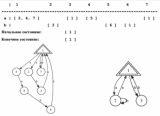
Рис. 2. Изображены графы состояний исходного недетерминированного автомата A1 и свернутого детерминированного A2.
Проблема вершинной минимизации недетерминированных конечных автоматов исследована в [3]. Предложенный подход состоит в построении специального отношения # и выделении эвристических правил в покрытии блоков и псевдоблоков этого отношения. Такое покрытие позволяет получить недетерминированный автомат, имеющий минимальное количество состояний, но в некоторых случаях построенный по этому покрытию автомат не будет эквивалентен исходному.
Для серии регулярных выражения (aaUaabbUaba)*b(aUb)k (для k ≥ 2) при увеличении k количество состояний ДКА, построенного по НДА, будет экспоненциально увеличиваться, а у соответствующего зеркального НДА и зеркального ДКА количество состояний увеличится пропорционально количеству букв справа от буквы b в вышеприведенном регулярном выражении. Сокращенная таблица позволяет найти НДА покрывающий, ДКА и имеющий наименьшее количество состояний. Его можно найти методом перебора, используя, так называемые гриды, покрывающие все состояния.
Таким образом, для бидерминированного автомата минимальный недетерминированный автомат будет единственным и совпадать ним. Для бидетерминированного автомата синтаксический моноид автомата будет обладать коммутирующими идемпотентами.
Заключение
В статье рассмотрены вопросы, связанные определением минимального множества, на котором действует синтаксический моноид недетерминированного автомата. Проведено его сравнение с бидетерминированными и обратимыми автоматами. Для минимизации предлагаются эвристические алгоритмы.
Список использованной литературы
- Мальцев А.И. Избранные труды. Т.1. М. Из-во Наука 1978. – 347 с.
- Хорпкрофт Дж., Р.Мотвани, Дж. Ульман «Введение в теорию автоматов. Языков и исчислений», Из-во «Вильямс», 2008. – 528 с.
- Мельников Б.Ф. Недетерминированные конечные автоматы.Тольятти. ТГУ, 2009. – 161 с.
- Лаллеман Ж. Полуруппы и комбинаторные приложения. – М. Мир, 1985. – 440 с.
- Pin, J.E. On reversible automata. In Proceedings of the fi rst LATIN conference, Lecture Notes in Computer Science 583, Springer, 1992. P. 401-416.
- Tamm Hellis, Ukkone Esko. Bideterministic automata and minimal representations of regular languages/ Hellis Tamm , Esko Ukkonen, // Proceedings of the 8th international conference on Implementation and application of automata. – Santa Barbara, CA, USA, – July 16-18, 2003. – P. 135-149.
- Прасолов В.В. Элементы комбинаторной и дифференциальной топологии. М: Из-во МЦНМО, 2004. – 352с.