Модальное управление электроприводом переменного тока

Приведена методика синтеза модальных регуляторов координат векторной системы «преобразователь частоты–асинхронный двигатель» методом стандартных уравнений. Дана оценка качества процессов регулирования координат путем анализа результатов имитационного моделирования системы в среде MatLab.

Ключевые слова: модальный регулятор, электропривод переменного тока, векторная система.

Теория систем векторного управления частотно-регулируемого асинхронного электропривода разработана достаточно полно [1]. Контуры регулирования в системе векторного управления выполняются, как правило, в соответствии с принципами подчиненного регулирования координат, что ограничивает их быстродействие и, как следствие, точность в динамических режимах. Обеспечить предельное быстродействие и точность в динамических режимах возможно, снабдив систему так называемым модальным регулятором, построенным на основе суммирования обратных связей по вектору состояния. Вопросы построения таких регуляторов применительно к векторным системам асинхронного электропривода в литературе отражены недостаточно, в связи с чем в данной работе ставится задача разработки методики проектирования модальных регуляторов векторных систем частотно управляемого асинхронного электропривода и проверка ее эффективности с помощью имитационного моделирования в среде MatLab.

В качестве объекта управления принята получившая наибольшее распространение система преобразователь частоты с автономным инвертором напряжения с широтно-импульсной модуляцией – асинхронный двигатель. Поскольку у таких преобразователей автономный инвертор формирует не только частоту, но и амплитуду выходного напряжения, влияние звена постоянного тока на динамические свойства системы при синтезе можно не учитывать. Кроме того, частота модуляции современных преобразователей весьма высока, что позволяет пренебречь также его дискретными свойствами. Изложенное дает возможность представить в первом приближении преобразователь частоты безынерционным линейным звеном с коэффициентом передачи k_п .

Математическая модель асинхронного двигателя (АД) с учетом общепринятых допущений [2], в декартовой системе координат u–v, вращающейся с произвольной скоростью ω_k, в форме Коши имеет следующий вид [3].

где u_1u, u_1v, i_1u, i_1v, Ψ_2u, Ψ_2v – проекции результирующих векторов напряжения статора u₁, тока статора i₁, потокосцепления ротора Ψ₂ соответственно, на оси u и v декартовой системы координат; ω = ω_эл/p_п – угловая скорость вращения ротора; ω_эл – угловая скорость вращения электромагнитного поля; M_с – момент статического сопротивления на валу двигателя [1].

Уравнения динамики АД в векторно-матричной форме имеют вид

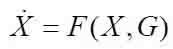
где X и G – векторы переменных состояния и входных воздействий, причем

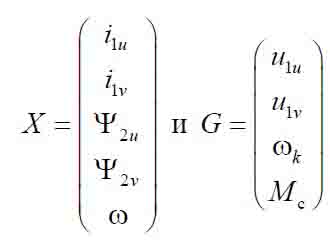
Линеаризованную модель АД будем искать в виде стандартной векторно-матричной формы уравнений состояния

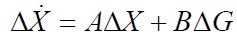
где A и B – матрицы динамики и входа соответственно, которые необходимо определить; ΔX и ΔG – приращения векторов переменных состояния и входных воздействий соответственно.

Применим метод линеаризации на основе разложения уравнений в ряд Тейлора. Тогда матрицы A и B определятся в виде

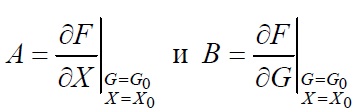
где X₀ и G₀ – переменные состояния и входные воздействия в точке установившегося режима (центра разложения), значения которых определяются по уравнениям статики.

Взяв производные от уравнений по соответствующим переменным, видим, что матрицы A и B имеют высокий порядок. Для их упрощения необходимо выбрать угловую скорость вращения ω_k системы координат u-v и сориентировать ось u по определенной векторной переменной АД.

Целесообразно использовать систему координат u–v с угловой скоростью вращения магнитного поля ω_k = ω_0эл , ориентированной по вектору потокосцепления ротора Ψ₂ = Ψ_2u , Ψ_2v = 0. Переменная ω_k = ω_0эл в этом случае определяется зависимостью ω_0эл = f(i_1v, Ψ_2u, ω), т. е. она уже не является входным воздействием.

Синтез модального регулятора проведем для управляющего воздействия, т. е. положим c M_c = 0. Наличие на входе двигателя преобразователя частоты учтем в матрице входа коэффициентом k_п. Если скомпенсировать влияние перекрестных обратных связей по току статора, получим матрицы

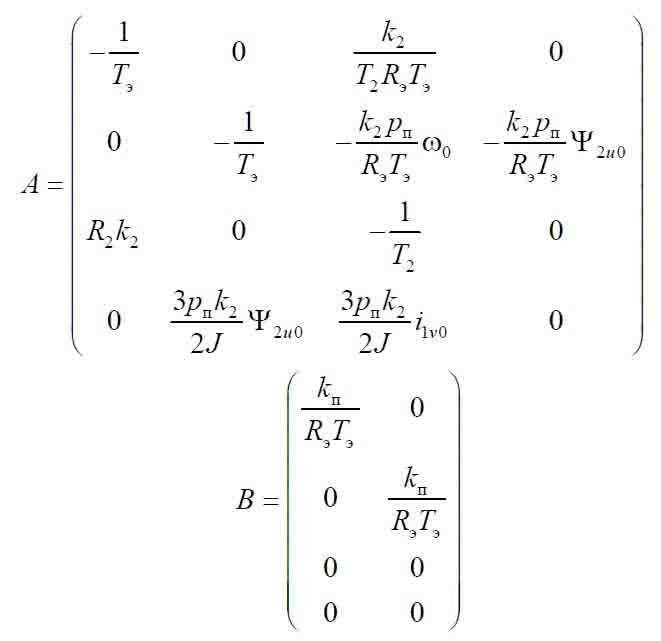
Расчет модальных регуляторов производится отдельно для двух каналов управления: канала регулирования потокосцепления ротора АД и канала регулирования скорости АД. Таким образом, строится два контура регулирования аналогично построению систем двухзонного регулирования скорости электропривода постоянного тока [1].

Разобьем матрицы динамики и входа на две пары для синтеза модальных регуляторов по каждому из каналов регулирования.

Матрицы канала регулирования потокосцепления ротора:

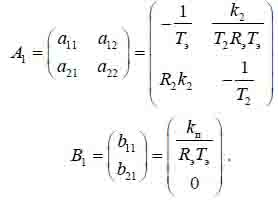
Матрицы канала регулирования скорости вращения ротора АД:

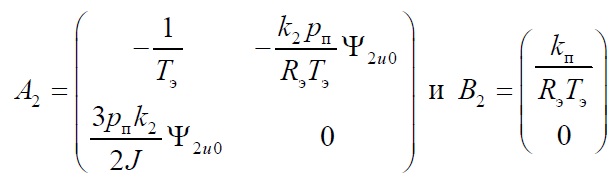
Характеристический полином замкнутого по вектору состояния объекта управления можно записать в виде

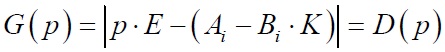
где K – коэффициент модального регулятора; E – единичная матрица; D(p) – желаемый характеристический полином.

Поскольку корни характеристического уравнения D(p)=0 определяют динамические свойства системы, замкнутой через модальный регулятор, то для получения желаемых динамических показателей требуется, чтобы замкнутая обратная связь по вектору состояния обеспечивала желаемые корни характеристического полинома. Таким образом, необходимо подобрать матрицу K модального регулятора так, чтобы получить в комплексной плоскости желаемое распределение корней характеристического полинома.

Синтез модального регулятора выполняется методом стандартных уравнений в нормированной форме [1]. Для получения нормированной формы исходное уравнение n-го порядка делится на коэффициент при старшей степени D0 и приобретает корневую форму:

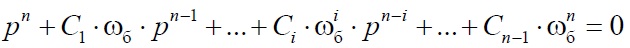
где ω_б – базовая частота (среднегеометрический корень)

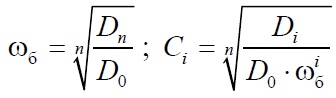
Делением уравнения на ω_бⁿ осуществляется переход к нормированному уравнению:

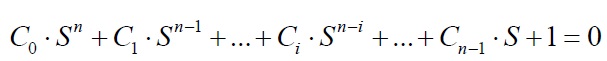
с относительным оператором

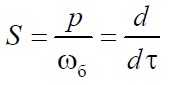
и относительным временем

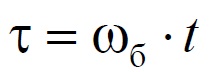
Рассчитаем коэффициенты обратных связей (ОС) при настройке системы на модульный оптимум: перерегулирование σ = 4.5%, а относительное время переходного процесса τ_п.п = 2.8 ω_б^-1. Нормированное желаемое уравнение имеет вид [1]

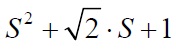
После перехода к абсолютным единицам подставим желаемый характеристический полином в выражение и приравняем значения коэффициентов при одинаковых степенях p, получим вектор коэффициентов модального регулятора для канала регулирования потокосцепления ротора:

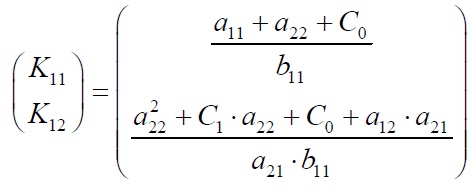
Аналогично производится расчет второго канала регулирования угловой скорости вращения ротора АД. В качестве примера принята настройка по биномиальному разложению (S+1)_n : перерегулирование σ = 0 %, а время переходного процесса τ_п.п = 4.8 ω_б^-1.

Приведем расчет переходных процессов в замкнутой системе асинхронного электропривода при помощи пакета имитационного моделирования Matlab фирмы The MathWorks, Inc. Воспользуемся соответствующей структурной схемой замкнутой системы асинхронного электропривода в неподвижной системе координат (рис. 1), в которой переменные ОЭМ характеризуют поведение реальных координат АД.

В схеме приняты следующие обозначения.

Модель АД, реализованная по уравнениям состояния – AD.

Коэффициенты усиления, обеспечивающие требуемые потокосцепление и скорость ротора АД при наличии ОС – k_1u, k_2u.

Блоки преобразователя координат – m₁, m₃, m₅, реализованные по уравнениям

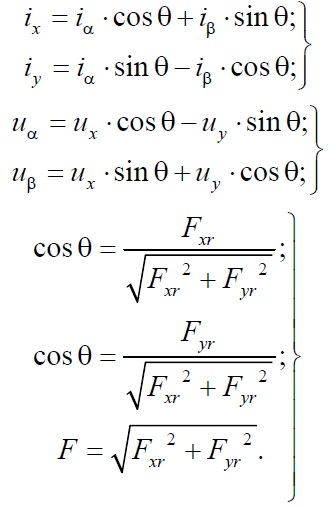
Блок компенсаций перекрестных связей – BK, реализованный по уравнениям

где U_yx, U_yy – управляющие воздействия на входе системы.

Переходные процессы в представленной модели изображены на рис. 2. Они совпадают с переходными процессами во вращающейся системе координат, что подтверждает правильность преобразования координат. Сначала подается задание на потокосцепление ротора АД, которое успешно отрабатывает канал регулирования потокосцепления, после чего производится скачкообразное изменение задания на скорость вращения ротора и включается в работу второй канал. И, наконец, на третьем участке осуществляется моделирование наброса нагрузки на валу АД.

Характер переходных процессов соответствует заданным настройкам. Следовательно, регуляторы позволяют обеспечить требуемый уровень скорости и потокосцепления как в неподвижной, так и во вращающейся системах координат.

Список использованной литературы

1. Терехов В. М., Осипов О. И. Системы управления электроприводов : учеб. для студ. высш. учеб. заведений; под ред. В. М. Терехова. М. : Академия, 2005.
2. Соколовский Г. Г. Электроприводы переменно-го тока с частотным регулированием : учеб. для студ. высш. учеб. заведений. М. : Академия, 2006.
3. Карагодин М. С., Федоренко А. А. Уравнения динамики частотно-управляемых электроприводов : учеб. пособие / Краснояр. политехн. ин-т. Красноярск, 1985.

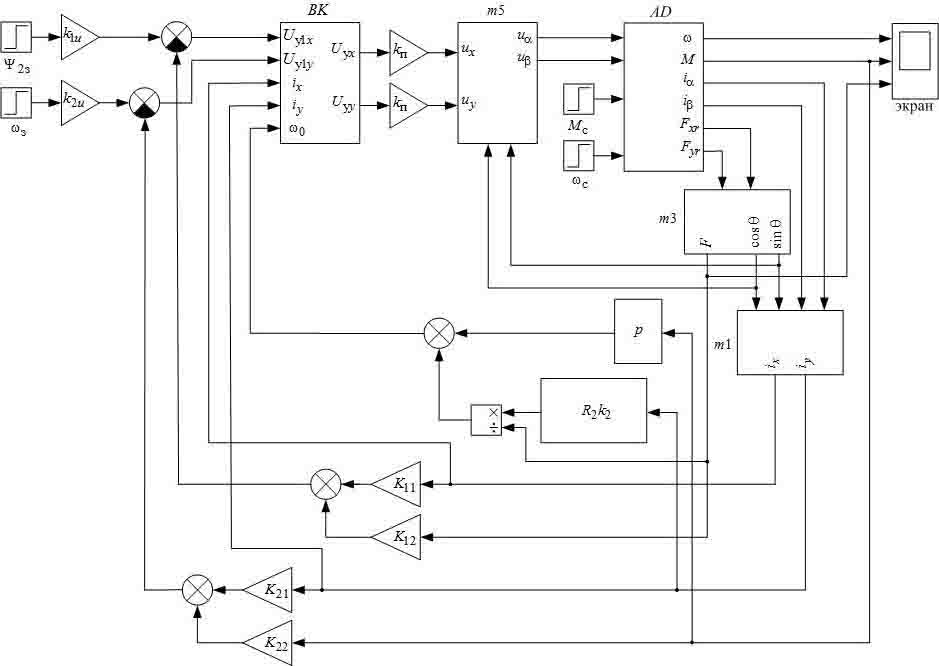
Рисунок 1 – Модель электропривода в неподвижной системе координат

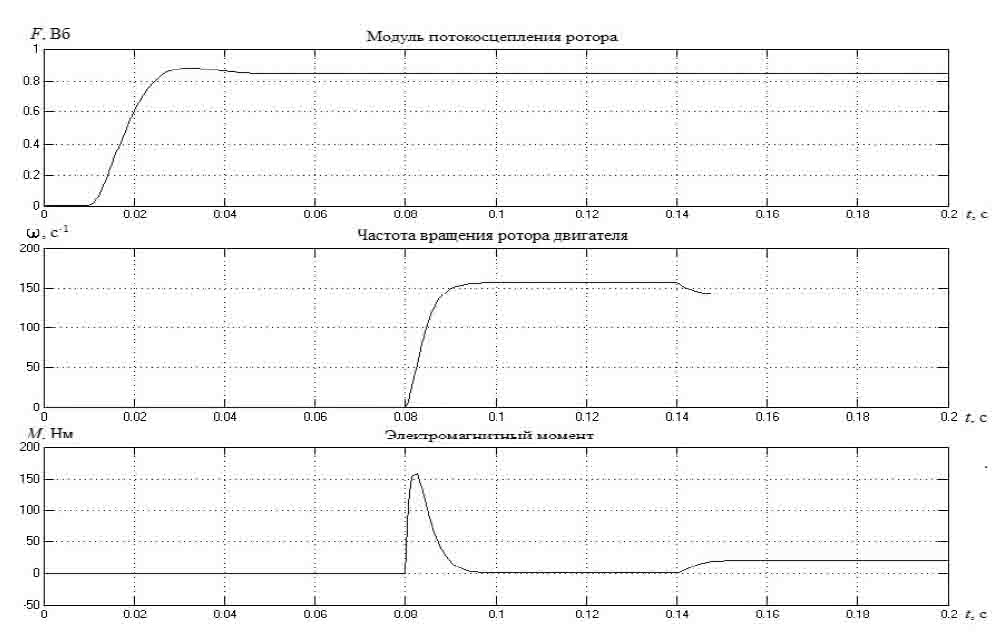
Рисунок 2 – Графики переходных процессов в неподвижной системе координат