Аннотация
Филинов Н.Ю. Применение теории нечетких множеств в выборе метода подземной добычи. Рассмотрены системы нечеткого управления. Исследована методика управления технологическим процессом с помощью нечеткого регулирования.
Вступление
Доступные залежи следует тщательно оценивать оптимальным образом. При этом выбор наиболее подходящего метода подземной добычи имеет большое значение с точки зрения экономики, техники и безопасности. В процессе выбора метода необходимо учитывать многие контролируемые и неконтролируемые параметры. Поэтому эти параметры должны быть получены с научно-техническими исследованиями для каждого месторождения руды. До настоящего времени исследования, посвященные методу отбора подземных горных пород, были проведенных многими учеными, такими как Босхов-Райт (1973), Хартман (1987), Лаубшер (1981), Николас-Нарек (1981).
Оценки классического метода обычно вызывают сложную ситуацию и занимают длительный период времени. Процесс принятия решений усложняется вопросом о многих параметрах и неопределенными элементами отбора метода подземных горных работ. Новые методы принятия решений позволили принимать решения более быстро, легко и обдуманно.
Теория нечетких множеств
Нечеткая логика является подходящей методологией для исследования ряда проблем, характеризующихся ненадежными данными, неточными измерениями, неоднозначным языком и нечеткими правилами принятия решений. За последние три десятилетия нечеткая логика была выдвинута как формальное средство обработки неявной неточности в широком спектре проблем, например, в области промышленного контроля, военных операций, экономики, инженерии, медицины, надежности, распознавании образов и классификации.
Инженеры по планированию шахт часто используют свою интуицию и опыт в принятии решений. Тем не менее, лица, принимающие решения, могут не знать, как бороться с такими количественными переменными, как слабый камень или руда с массивными размерами. Неопределенность, о которой идет речь, может быть легко оценена путем применения теории нечетких множеств в процессе принятия решений. Нечеткое множество можно охарактеризовать как назначение ценности, которое показывает степень участия в нечетком множестве независимо от существования в словарном множестве. Степень принадлежности показывает степень адаптации к свойствам, которые описываются нечетким множеством этого существования. Не существует точного определения между элементами нечеткого множества и внешнего остатка этих элементов. Таким образом, нечеткое множество может быть описано как понятия / объекты, имеющие неопределенные пределы между ними. А именно, теория нечетких множеств интересуется нечеткостью, которая появляется в этих неопределенных пределах. В качестве примеров этой нечеткости можно привести высокую температуру и небольшие числа.
В классической теории множеств элемент является либо элементом множества, либо нет. Нет частичной принадлежности. Эту ситуацию можно объяснить примером, приведенным на рисунке 1. В этом примере температуры ниже 30°C не считаются горячими. В соответствии с этим даже 29,5°C не считается горячим. Поэтому в этой логике нет гибкости. В реальном мире эти ограничения не столь резкие. Необходимо, чтобы события имели определенную гибкость. Резкие пределы двусторонних переменных смягчаются нечеткой логикой с применением гибких характеристик. На рисунке 2 показана теория нечетких множеств, которая дает значение переменных, таких как температура, близкая к величине, наблюдаемой в реальном мире. В соответствии с этим, степень участия горячего нечеткого множества выявляется при значениях температуры от 20 до 40°C. Степень членства постепенно уменьшается от 1 до 30°C до 0 при 20°C. Согласно рисунку 2, при снижении температуры появляется небольшое горячее состояние. Например, температура 25°C квалифицируется как мало горячая, а температура 30°C считается очень горячей, а температура 20°C не является горячей. Поэтому температура 20°C не является элементом горячего нечеткого множества.
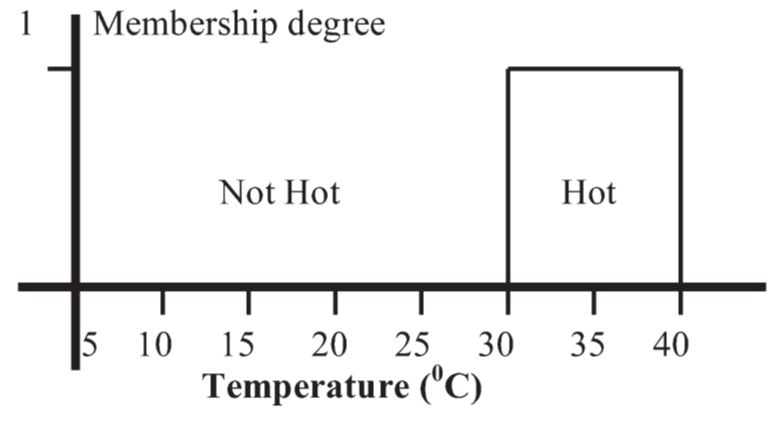
Рисунок 1 – Классическая теория
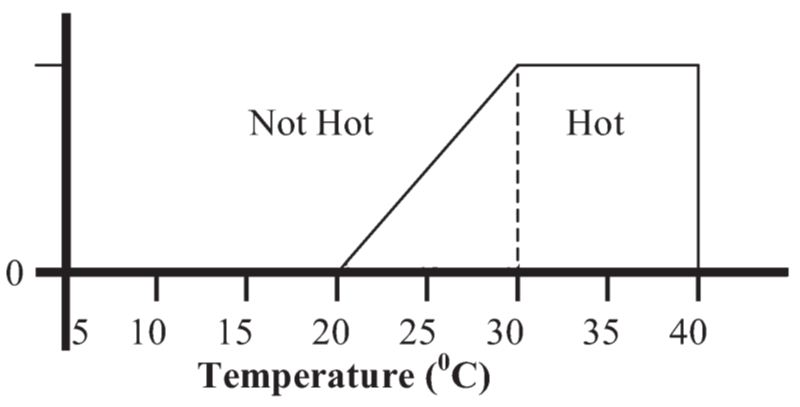
Рисунок 2 – Теория нечеткого множества
Следующий шаг теории нечетких множеств приведен на рисунке 3. На этом рисунке степень нечеткого набора множеств получает принадлежность к холодному в единицах 0.5. Степень принадлежности холодного нечеткого множества увеличивается, когда температура уменьшается. В соответствии с этим температура от 0 до 15°C считается очень холодной, и эта часть имеет холодное нечеткое множество всего членства. Существует постепенная принадлежность в холодном нечетком множестве для температуры от 15°C до 25°C. Следовательно, существует пересечение холодных и горячих нечетких множеств при температуре от 20°C до 25°C. Элементы в этой части могут быть взяты как члены либо горячего, либо холодного нечеткого множества.
Хотя эти примеры действительны для не-нечетких входов, иногда входы могут быть нечеткими в нечеткой логике. В этой ситуации степень принадлежности нечетких множеств определяется из области, охватываемой между нечетким множеством и нечетким входным значением. Эта ситуация показана на рисунке 4, а степень принадлежности составляет около 0,3.
Нечеткое принятие нескольких атрибутов
Принятие решений объясняется как процесс выбора лучшей альтернативы альтернативных наборов для достижения цели или целей. Существует много методов принятия решений. Основное внимание в этой статье уделяется методу Ягера, который является одним из методов принятия нечетких множественных атрибутов. Этот метод также основан на процессе аналитической иерархии (AHP).
AHP, разработанный Томасом Саати (1988), успешно используется на практике для решения различных проблем, связанных с принятием решений и планированием. Этот метод также использовался для решения проблемлиц, принимающих решения, в различных областях, таких как политика, оборона, градостроительство, связь и психология.
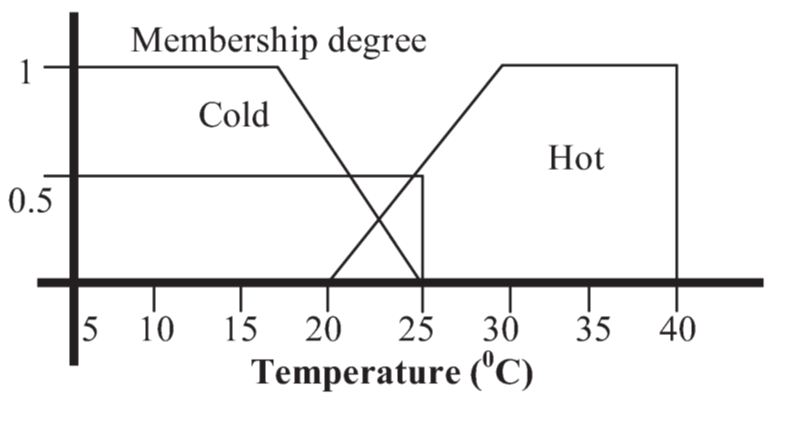
Рисунок 3 – Охват нечеткого множетсва
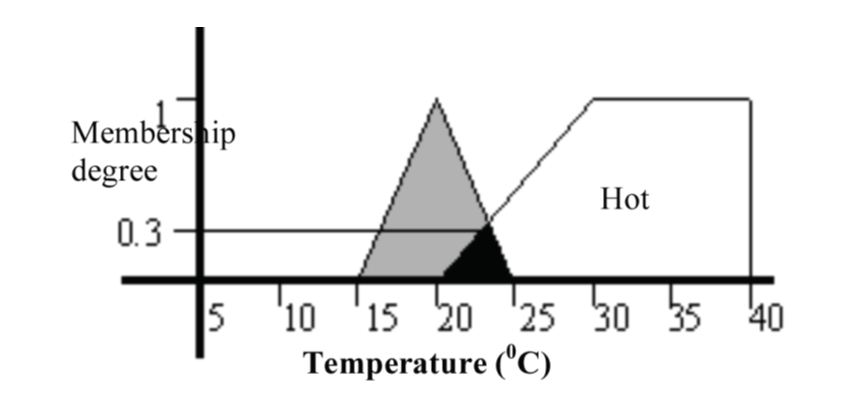
Рисунок 4 – Степень принадлежности нечетких входных значений
AHP основан на том, что проблемы можно решить более эффективно, разделив проблемы на правдоподобные и более мелкие части. Этот процесс формируется на следующих этапах.
- Четкое описание проблемы
- Определение подцелей
- Определение факторов, влияющих на подцели
- Анализ результатов модели по альтернативам.
Разработка Саати математического анализа парных сравнений ответов пользователей продолжала оказывать глубокое влияние на компьютерные приложения, предназначенные для улучшения интерактивного человеческого познания. Саати обнаружил что если пользователям предлагается измерить вклад одного или нескольких элементов принятия решения в два или более потенциальных решения, и если оценки элементов принятия решения вводятся попарно в двумерной матрице по мере их получения от пользователя, тогда матрица ответа может решаться по его главному собственному значению и для собственного вектора, содержащего это главное собственное значение. Эти математические решения дают прямые оценки согласованности данных в матрице отклика и нормализованная оценка вклада каждого элемента решения в каждое потенциальное решение. Использование метода собственных векторов также сохраняет порядковый ранг каждого из элементов принятия решения, когда данные в матрице ответа являются неполной или непоследовательной ситуации, часто встречающейся во время оценки выбора системы.
Практический эффект такого матричного познания во время оценки отбора заключается в том, чтобы регистрировать выбор пользователя потенциальных решений для рассмотрения, выбор пользователем элементов принятия решений для анализа и выбор пользователем консультантов для участия в анализе. Затем каждому консультанту предлагается оценить количественный вклад каждого элемента решения в каждое потенциальное решение, а затем эту оценку взвешивают с помощью рассчитанного собственного вектора, полученного путем решения матрицы ответа каждого консультанта. Затем каждое количественное масштабирование каждого консультанта каждого потенциального решения рассчитывается, упорядочивается по порядку и в сочетании с результатами других консультантов, чтобы дать приемлемое решение на основе консенсуса и ранжирование альтернативных решений.
Формально пусть A = _A1, A2, ..., An_ - множество альтернатив, C = _C1, C2, ..., Cm_ - множество критериев, которые
могут быть заданы как нечеткие множества в пространстве альтернатив, а G цель, которая также может быть задана
нечетким множеством. Во-первых, степени участия альтернатив для каждого критерия определяются экспертными взглядами.
Рассмотрим простой пример:
G = [0.5/A1, 0.8/A2, 0.3/A3]
C1 = [0.7/A1, 0.9/A2, 0.5/A3]
C2 = [0.4/A1,
0.2/A2, 0.9/A3]
Для определения весовых коэффициентов мы использовали шкалу оценки, определяемую лицом, принимающим решения. Ягер предлагает использовать метод Саати для парного сравнения критериев (атрибутов). Паровое сравнение атрибутов (критериев) могло бы улучшить и облегчить оценку важности критериев. Саати разработал процедуру получения шкалы отношений для сравниваемых элементов.
Для оценки важности лица, принимающего решение (w), предлагается судить о критериях при попарных сравнениях и назначенных значениях wij = 1 / wij. Где i - номер столбца, а j - номер строки в матрице m x m. Получив суждения, матрица m x m B построена так, что: (a) bii = 1; (b) bij = wij; (c) bji = bij14. Подводя итог, Ягер предполагает, что результирующий собственный вектор должен использоваться для выражения эмпирической оценки важности принятия решения. Взаимная матрица, в которой значения даются инициатором принятия решений по каждому критерию в решении и критериям 1 и 2, соответственно C1 и C2, три раза так же важны, как и G, а встречная матрица попарного сравнения:
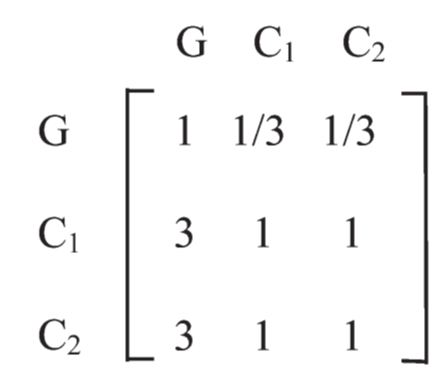
Следовательно, собственные значения обратной матрицы lambda = [0, 3, 0] и, следовательно, lambda_max = 3. Все значения, кроме одного, равны нулю (как указано Саати). Весовые коэффициенты, наконец, образуются в собственном векторе матрицы.

Собственный вектор соответствует весам, которые должны быть связаны с принадлежностью каждого атрибута / объекта
/ цели. Таким образом, экспоненциальное взвешивание a1 = 1/3, a2 = 2/3, a3 = 2/3, а окончательное решение (функция
принятия решения о членстве) относительно местоположения сайта дается следующим образом:
uD(A) = D(A) = min
_uG(X), uC1(X),
uC2(X),……,uCM(X)
Существуют некоторые случаи, когда важность критериев не одинакова, и требуются весовые коэффициенты. Функция решения с относительной важностью критериев, опуская сигнал принадлежности u для упрощения, равна:
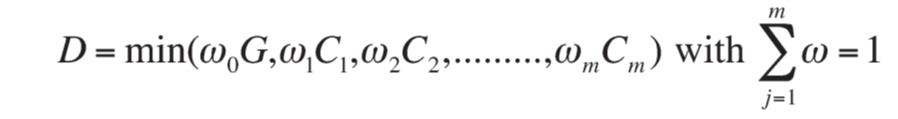
Таким образом, функция нечеткого решения в примере
D(A) = min_G1/3, C12/3, C22/3
G = [0.5/A1, 0.8/A2,
0.3/A3]0.229 = [0.85/A1, 0.95/A2, 0.76/A3]
C1= [0.7/A1, 0.9/A2, 0.5/A3]0.688 = [0.78/A1, 0.93/A2, 0.62/A3]
C2= [0.4/A1, 0.2/A2, 0.9/A3]0.688 = [0.53/A1, 0.33/A2, 0.93/A3
D(A) = 0.53/A1, 0.33/A2, 0.62/A3
и оптимальное решение, соответствующее максимальной принадлежности
0.62, равно A3
(D(A*) D(A) = 0.62/A3).
Список использованной литературы
1. KAHRIMAN, A., CEYLANOGLU, A., DEMIRCI, A., ARPAZ, E., and UYSAL, O. Optimum underground
mining method selection for Kayseri-Pulpinar Chrome Mine, Mining Review, TMMOB Chamber of The Mining Engineers,
Ankara, 1994. pp. 27–41.
2. DEMIRCI, A., CEYLANOGLU, A., and KAHRIMAN, A. Determination of optimum underground
mining method at Aegean Metal Eskisehir Chrome Enterprise and Projected Studies, Final Report, Cumhuriyet Universiy,
Sivas, 1995.
3. NICHOLAS, D.E. Selection variables, Mining Engineering Handbook, vol. 2, 1993. pp. 2051–2057.
4.
HAMRIN, H. Choosing an underground mining method, Techniques in Underground Mining, Society of Mining Metallurgy
and Exploration Inc., Littleton, CO, USA, 1998. pp. 45–85.
5. BASCETIN, A. A decision support system using
analytical hierarchy process (AHP) for the optimal environmental reclamation of an open pit mine, Environmental
Geology, vol. 52, no. 4, April, 2007, pp. 663–672.
6. BASCETIN, A., OZTAS, A., and KANL?, A. EQS: A Computer
Software Using Fuzzy Logic for Equipment Selection in Mining Engineering, The Journal of the South African Institute
of Mining and Metallurgy (SAIMM), vol. 106. no. 1, January, 2006.
7. BASCETIN, A. An Application of the Analytic
Hierarchy Process in Equipment Selection at Orhaneli Open Pit Coal Mine. Transactions of the Institutions of
Mining and Metallurgy (AusIMM), Section A-Mining Technology. vol. 113, no. 3, September, 2004.
8. ZADEH,
L.A. The concept of a linguistic variable and its application to approximate reasoning, Part 1, Information Science,
vol. 813, 1975. pp. 199–249.
9. GOKAY, M.K. Used of the fuzzy logic approach on rock mass classification,
Mining Review, TMMOB Chamber of The Mining Engineers, Ankara, 1998. pp. 3–11.
10. KARADOGAN, A., BASCETIN,
A., KAHRIMAN, A., and GORGUN, S. A new approach in selection of underground mining method, Int. Conf. Modern
Management Mine Producing Geol. Env. Protection, Varna, Bulgaria, June 3–9, 2001. pp. 171–183.
11. BASCETIN,
A. and KESIMAL, A. Fuzzy logic application in mining, Engineering Faculty’s Earth Sciences Review, vol. 12, no.
1, 1999.
12. ALBAYRAK, C. and ALBAYRAK, E. Selection of rigth associate on strategical cooperation: suggestion
a decision support model, 1th National Production Researchs Sym., Istanbul, 1997. pp. 19–22.
13. YAGER, R.R.
A new methodology for ordinal multi objective decisions based on fuzzy sets, Decision Sci. 12, 1981. pp. 589–600.
14.
SAATY, T.L. Exploring the interface between hierarchies, multiple objectives and fuzzy sets, Fuzzy Sets and Systems,
1, 1978. pp. 57–68.
15. Matlab, The Mathworks, Inc., version 5.0.0.4069, copyright 1984–1996.