Реферат за темою випускної роботи
Зміст
- Введення
- 1. Актуальність теми
- 2. Мета і завдання дослідження, плановані результати
- 3. Огляд досліджень і розробок
- 4 Приклади перекидання дуг
- 5 Аналіз основних видів кінцевих автоматів
- 5.1 Детермінований кінцевий автомат
- 5.2 недетермінірованного кінцевий автомат
- 6 Висновки
- Список джерел
Введення
Кінцевий автомат (state machine) – модель, яку зручно використовувати в найрізноманітніших галузях, починаючи від моделювання логічних пристроїв в технічної діагностики та закінчуючи структуруванням додатків. В Зокрема, одним з додатків кінцевих автоматів є моделювання несправностей дискретних пристроїв. Часто такі несправності можна описати як перекидання дуг в автоматі при збереженні вихідних реакцій.
Представляють інтерес такі перекидання, які змінюють поведінки автомата. Відомий ряд робіт, в яких досліджуються властивості перекидань такого роду. У даній роботі триває дослідження властивостей автоматів, схильних до перекидання дуг і спостереження за подальшою його деградацією.
1. Актуальність теми
Модель кінцевого автомата пройшла хорошу перевірку часом. Використання кінцевих автоматів дозволяє розробникам створювати добре організовані логічні системи з гнучкими можливостями, а також аналізувати їх поведінку в різних умовах.
Наприклад, в іграх часто використовують різні персонажі, які переміщаються в області гри і можуть діяти в різних режимах. Використання кінцевих автоматів з чітко визначеними правилами для кожного персонажа, визначальними можливі варіанти його поведінки в різних станах і допустимі переходи з одного стану в інше, дозволяє створювати складні варіанти поведінки як персонажів, керованих комп'ютером, так і персонажів, керованих користувачем [ 1 ].
Ця робота відноситься до теорії експериментів з автоматами. експериментом називають процес подачі на автомат послідовності вхідних сигналів, спостереження відповідної реакції автомата і висновок висновку про функціонуванні і властивості автомата, заснованих на цих спостереженнях і апріорної інформації про автомат. Основне завдання теорії експериментів полягає в розробці ефективних експериментів, що дозволяють отримати певні відомості про будову автомата, його функціях, про характеристики процесу перетворення інформації, здійснюваного цим автоматом.
Таким чином, дослідження моделі кінцевого автомата і вивчення його поведінки є актуальним завданням.
2. Мета і завдання дослідження, плановані результати
Об'єктом дослідження є поведінка кінцевого при перекиданні дуг.
Предметом дослідження є дослідження методу побудови функції деградації поведінки кінцевого автомата в результаті перекидання дуг.
Метою магістерської дисертації є розробка і дослідження методу побудови функції деградації поведінки кінцевого автомата в результаті перекидання дуг.
Основні завдання роботи:
- провести аналіз поведінки кінцевого автомата в результаті перекидання k-дуг (мал. 1);
- з'ясувати існування допустимих k-перекидань і описати структуру автоматів, що допускають їх;
- розробити алгоритм побудови допустимих k-перекидань;
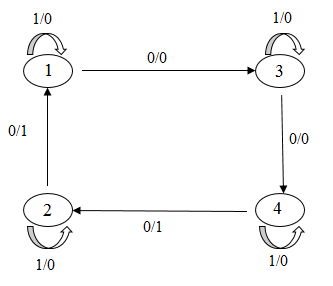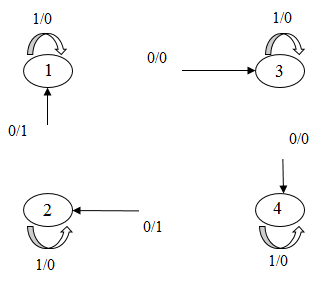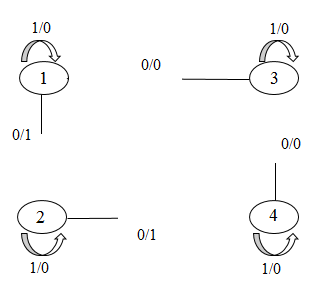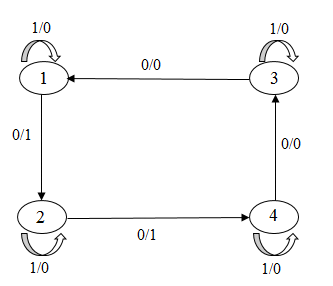
Малюнок 1 – Перекидання 4-х дуг в автоматі
(анімація: 17 кадрів, 3 цикли повторення, 82,1 кілобайт)
3. Огляд досліджень і розробок
Автомати, близькі по поведінці в тому чи іншому сенсі, досліджуються досить давно, так само, як і структура класів таких автоматів. В основному, це завдання розглядається в рамках теорії експериментів з автоматами.
Підстава теорії експериментів з автоматами було покладено Муром. У його роботах дослідження проводилося в двох напрямках: неотличимой автоматів ніяким кратним і ніяким простим експериментом, а також розпізнавання автомата і його станів за допомогою таких експериментів. Надалі теорія експериментів отримала розвиток в роботах Ф. Хенні, Милі, Брауера і інших. Методи і результати аналізу автоматів і алгоритмів проведення експериментів з ними досить повно представлені у відомій книзі А. Гілла.
Вітчизняні роботи в області експериментів з автоматами пов'язані з іменами A.M. Богомолова та його учнів, М.П. Василевського, В.Н. Носкова, Н.В. Євтушенко, А.Ф. Петренко, І.К. Рисцова, В. А. Твердохлебова, С.В. Яблонського, В.Б.Кудрявцева і ін.
Теорія експериментів інтенсивно розвивається і в даний час. В [2-4] отримано ряд результатів, пов'язаних з аналізом поведінки автоматів в умовах впливу на них факторів зовнішнього середовища. У ряді робіт вивчався вплив перекидань дуг на поведінку автомата. В теорії графів також розглядалися родинні завдання, де вивчалася задача визначення, коли один з графів (автомат) може бути отриманий з іншого в результаті деякої послідовності перекидань дуг.
4. Приклад перекидання дуги
Нагадаємо, що перекидання однієї дуги завжди призводить до неізоморфних автомату. Легко навести приклади, коли перекидання в автоматі двох дуг також породжує новий автомат, що не ізоморфний вихідного.
В [4] були сформульовані достатні умови збереження поведінки автоматом при перекиданні двох дуг, і було показано, що для будь-якого натурального k > 1 існує наведений автомат, в якому знайдеться підмножина з k дуг, одночасна перекидання яких призводить до ізоморфного автомату. В [5] було доведено, що при перекиданні двох дуг вхід-вихідні позначки на цих дугах збігаються. Там же були наведені приклади не сильно зв'язкових автоматів, що допускають перекидання декількох дуг, і було висловлено припущення, про те, що стану, з яких перекидаються дуги, недосяжні з тих станів, куди спрямована перекидання.
Наведемо ряд прикладів, коли перекидання не змінює поведінки вихідного автомата.
Граф А '(див. мал.2) є результатом перекидання двох дуг в графі А: дуга (6, 0, 0, 8) перекидається в стан 9 і замінюється дугою (6', 0, 0, 9 ') , дуга (7, 0, 0, 9) замінюється дугою (7 ', 0, 0, 8'). Неважко бачити, відображення : А > А ', при якому (1) = 1'; (2) = 2 '; (3) = 3 '; (4) = 4'; (5) = 5 '; (6) = 7 '; (7) = 6 '; (8) = 8 '; (9) = 9 ', є изоморфизмом графа А на граф А'.
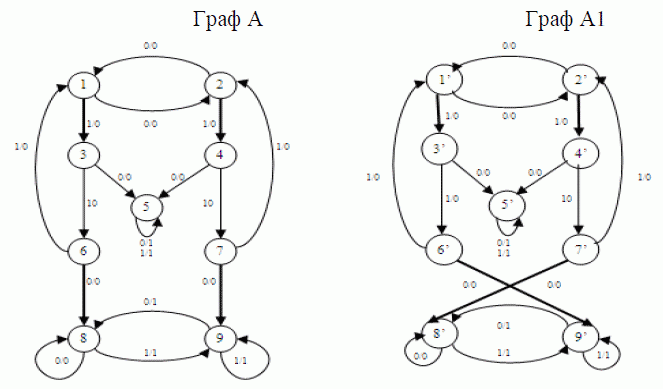
Малюнок 2 – Приклад ізоморфізму автоматів при перекиданні двох дуг
В даному прикладі компоненти сильної зв'язності автомата А - це безлічі станів {1,2,3,4,6,7}, {5}, {8,9}, і перекидає дуги прилягають різних компонентів.
5. Аналіз основних видів кінцевих автоматів
5.1 Детермінований кінцевий автомат
Детермінованим кінцевим автоматом (ДКА) називається машина, що розпізнає ланцюжка символів, в якій для кожної послідовності вхідних символів існує лише один стан, в яке автомат може перейти з поточного (мал. 3). Вона має вхідну стрічку, розбиту на клітини, головку на вхідних стрічці (вхідні головку) і керуючий пристрій з кінцевим числом станів. Кінцевий автомат М можна представити у вигляді п'ятірки (S, L, a, s, F), де
- S – кінцеве безліч станів пристрої управління;
- L – алфавіт вхідних символів;
- a – функція переходів, що відображає S x (I U {i}) в безліч підмножин множини S;
- s – початковий стан пристрою управління;
- F – безліч заключних (допускають) станів [5].
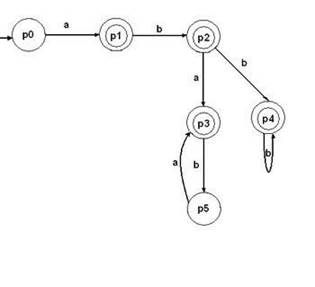
Малюнок 3 – Детермінований кінцевий автомат
ДКА виконує кроки, які визначаються поточним станом його блоку керування та вхідних символом, розглядаємим вхідний головкою. кожен крок складається з переходу в новий стан і зсуву вхідної головки на одну клітку вправо. Що мова представимо регулярним виразом тоді і тільки тоді, коли він допускається деяким кінцевим автоматом [6].
Кінцевий автомат можна описати за допомогою діаграм станів і таблиць переходів.
Діаграма станів (або іноді граф переходів) – графічне представлення безлічі станів і функції переходів. Являє собою навантажений односпрямований граф, вершини якого – стану КА, ребра - переходи з одного стану в інший, а навантаження – символи, при яких здійснюється даний перехід. Якщо перехід зі стану а1 в А2 може бути здійснений при появі одного з декількох символів, то над дугою діаграми (гілкою графа) повинні бути надписані всі вони [7].
Таблиця переходів – табличне представлення функції F. Зазвичай в такій таблиці кожному рядку відповідає один стан, а одну - один допустимий вхідний символ. В осередку на перетині рядка і стовпця записується дію, яку повинен виконати автомат, якщо в ситуації, коли він перебував в даному стані на вході він отримав даний символ.
5.2 недетермінірованного кінцевий автомат
Недетермінірованного кінцевий автомат – абстрактна машина, яка читає символи з вхідного ланцюжка і вирішує, допустити або відкинути цей ланцюжок. Він може змінити стан, перейшовши з одного стану в інший. Внутрішню структуру такого автомата можна уявити графом переходів НКА теж розпізнає ланцюжка символів, ланцюжок вважається допустимою, якщо після її обробки безліч станів, в якому опинився автомат, містить хоча б одне допускає. Таким чином, НКА також задає певний мову [8].
Будь-недетермінований кінцевий автомат може бути перетворений в детермінований так, щоб їхні мови збігалися і такі атомати називаються еквівалентними. Однак, оскільки кількість станів в еквівалентному ДКА в гіршому випадку зростає експоненціально з ростом кількості станів вихідного НКА, на практиці подібна детермінізації не завжди можлива. Крім того, кінцеві автомати з виходом в загальному випадку не піддаються детермінізації.
Для кожного стану і кожного вхідного символу НКА має нуль або більше варіантів вибору наступного кроку. Він може також вибирати, зрушувати йому вхідні головку при зміні стану чи ні [9]. Наведемо визначення недетермінірованного кінцевого автомата.
Існує додатковий результат або можливість зіставити якомусь взятому НКА еквівалентну «детерміновану» машину. Однак детермінований кінцевий автомат, еквівалентний даному НКА з n станами, може мати аж до 2 в n ступеня станів. Тому перехід від НКА до детермінованого автомату не завжди дає ефективний спосіб моделювання недетермінірованного кінцевого автомата [10].
Висновки
Ідея застосування кінцевих автоматів є надзвичайно корисною концепцією, плідність якої пройшла перевірку часом. Використання кінцевих автоматів дозволяє розробникам створювати добре організовані додатки з гнучкими можливостями. Їх застосування дозволяє створювати ясний, зрозумілий і надійно функціонує код.
Використання кінцевих автоматів стало вже звичайною практикою при проектуванні додатків для настільних комп'ютерів, серверів і мобільних пристроїв.
Переваги, які забезпечує застосуванням кінцевих автоматів, найпомітніше проявляються в разі додатків для мобільних пристроїв, вимагають економного расходиванія екранного простору, пам'яті, обчислювальної потужності і інших ресурсів.
Список источников
- Смирнова Н.В., Смирнов В.В. Применение теории конечных автоматов в разработке программных систем / Н.В. Смирнова, В.В., Смирнов // Збірник наукових праць Кіровоградського національного технічного університету. Техніка в сільськогосподарському виробництві, галузеве машинобудування, автоматизація. – 2014. – Вип. 27. – С. 316-320.
- Капитонова Ю.В. Основы дискретной математики / Ю.В. Капитонова, С.Л. Кривий, А.А. Летичевский, Г.М. Луцкий, Н.К. Печурин. – К.: Наукова думка, 2002. – 568 с.
- Евтушенко Н.В., Петренко А.Ф. Метод построения проверяющих экспериментов для произвольного недетерминированного автомата / Н.В. Евтушенко, А.Ф. Петренко // Автоматика и вычислительная техника. – 1990. – № 5. – С. 73-76.
- Кудрявцев В.Б., Грунский И.С., Козловский В.А. Анализ поведения автоматов / В.Б. Кудрявцев, И.С. Грунский, В.А. Козловский // Дискретная математика. – 2009. – №1. – С. 3-35.
- Козловский В.А., Копытова О.М. Представления автоматов относительно m-плотных классов / В.А. Козловский, О.М. Копытова // Матер. VIII Межд. семинара «Дискретная математика и ее приложения» (Москва, 2-6 февраля 2004 г.) – М.: Изд. МГУ. – С. 277-280.
- Швец О.С., Копытова О.М. О сравнении поведения ОДk-эталона и автоматов, порождаемых его локальными преобразованиями / О.С. Швец, О.М. Копытова // Материалы V всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых «Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2014)» (22.04-23.04.2014). Донецк: ДонНТУ, 2014. – С. 365-369.
- Паулин О.Н. Основы теории алгоритмов: учебное пособие / О.Н. Паулин. – Одесса: Автограф, 2005. – 188 с.
- Гилл А. Введение в теорию конечных автоматов / А. Гилл. – М.: Наука, 1966. – 272 с.
- Брауэр Р. Введение в теорию конечных автоматов/ Р. Брауэр. – М.: Радио и связь, 1987. – 392 с.
- Евтушенко Н.В., Лебедев А.В., Петренко А. Ф. О проверяющих экспериментах с недетерминированными автоматами / Н.В. Евтушенко, А.В. Лебедев, А.Ф. Петренко // Автоматика и вычислительная техника. – 1991. – № 6. – С. 81-85.
