Реферат по теме выпускной работы
Содержание
- Введение
- 1. Цель и задачи исследования, планируемые результаты
- 2. Обзор исследований и разработок
- Выводы
- Список источников
Введение
1. Цель и задачи исследования, планируемые результаты
В традиционной постановке задача синтеза оптимального управления в пространстве состояний предусматривает определение вектора управляющих сигналов u0(t) на основании минимизации некоторого критерия качества и формулируется следующим образом.
Для объекта управления, который описывается векторными дифференциальным и ал-гебраическими уравнениями
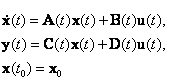 |
(9.1) |
необходимо найти закон управления u0(t), при котором достигается минимум квадратичного функционала качества
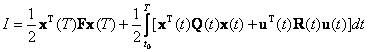 |
(9.2) |
который подробно представлен в лекции 7.
Общая математическая постановка указанной задачи приводит к уравнению Беллма-на, которое имеет следующий вид:
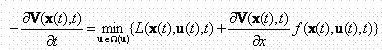 |
(9.3) |
Вывод уравнения Беллмана, характеристики входящих в него переменных и функций приведены в приложении 1.
Решение уравнения (9.3) для объекта управления, который описывается векторно-матричной моделью (9.1), позволяет определить закон оптимального управления в виде
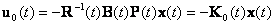 |
(9.4) |
где 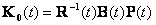 , P(t) - решение матричного дифференциального уравнения Рик-кати
, P(t) - решение матричного дифференциального уравнения Рик-кати
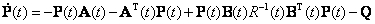 |
(9.5) |
c граничным условием 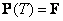 .
.
2. Обзор исследований и разработок
Вывод уравнения Риккати приведен в приложении 2.
В соответствии с вышеизложенным алгоритм синтеза оптимального уравнения пред-ставляет собой следующую последовательность действий:
1) построение векторно-матричной модели ОУ (9.1);
2) выбор элементов весовых матриц F, Q(t), R(t) в (9.2), при которых переходные процессы в системе управления удовлетворяют заданным требованиям;
3) решение матричного дифференциального уравнения Риккати (9.5);
4) анализ динамических характеристик в оптимальной системе управления и оценка ее качества.
Основные трудности возникают здесь при решении матричного дифференциального уравнения Риккати. Интегрирование этого уравнения удобно выполнять в обратном времени 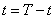 . В этом случае задача сводится к задаче Коши с начальными условиями
. В этом случае задача сводится к задаче Коши с начальными условиями 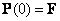 . Ввиду симметричности матрицы P(t) уравнение (9.5) равносильно системе n(n+1)/2 обыкно-венных нелинейных дифференциальных уравнений первого порядка с переменными во вре-мени коэффициентами.
. Ввиду симметричности матрицы P(t) уравнение (9.5) равносильно системе n(n+1)/2 обыкно-венных нелинейных дифференциальных уравнений первого порядка с переменными во вре-мени коэффициентами.
Для стационарных систем, в которых A, B, Q, R - коэффициентные матрицы и 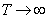 , матричное дифференциальное уравнение Риккати вырождается в алгебраическое
, матричное дифференциальное уравнение Риккати вырождается в алгебраическое
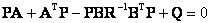 |
(9.6) |
решением которого является симметричная положительно определенная матрица Р.
Решение уравнения (9.28) для стационарных систем при 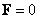 и
и 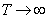 имеет предел
имеет предел
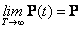 |
(9.7) |
Поэтому матрицу Р можно вычислить как предельное значение решения уравнения (9.5) при достаточно большом Т.
По аналогии с (9.4) оптимальное управление определится из выражения
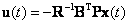 |
(9.8) |
Достоверность представленных алгоритмов подтвердим практическим примером.
Пример 9.1. Для электромеханического объекта с упругой передачей механического движения от вала электродвигателя к валу рабочего механизма, численные значения пара-метров которого приведены в табл. 9.1., выполним синтез оптимального управления (9.4) и безынерционного регулятора состояния.
Таблица 9.1. Параметры электромеханического объекта

Результатом серии вычислительных экспериментов явились:
- внутреннее содержание весовых матриц Q, и R
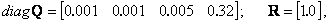
- временные характеристики
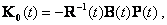
полученные в результате решения уравнения Риккати (9.5) в обратном времени, которые приведены на рис. 9.1
Для постановки имитационных экспериментов используем приведенные в табл. 9.2 постоянные расчетные значения коэффициентов обратных связей, соответствующие t=0, и значения реализации.
Таблица 9.2. Значения коэффициентов обратных связей

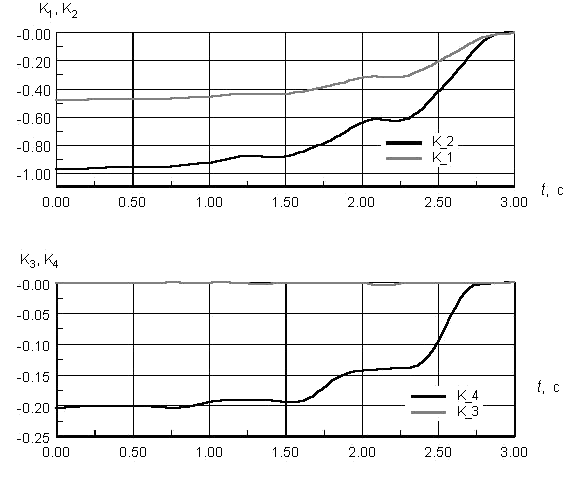
Рис. 9.1. Динамические характеристики K0(t)
Сравнительные динамические характеристики (см. рис. 9.2), систем управления, в ко-торых параметры регулятора соответствуют значениям реализации коэффициентов обратных связей (табл. 9.2) и значениям регулятора состояния, синтезированного при использовании в качестве критерия качества биномиального распределения корней (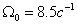 ), подтвер-ждают корректность алгоритмического и программного обеспечения синтеза оптимального управления.
), подтвер-ждают корректность алгоритмического и программного обеспечения синтеза оптимального управления.
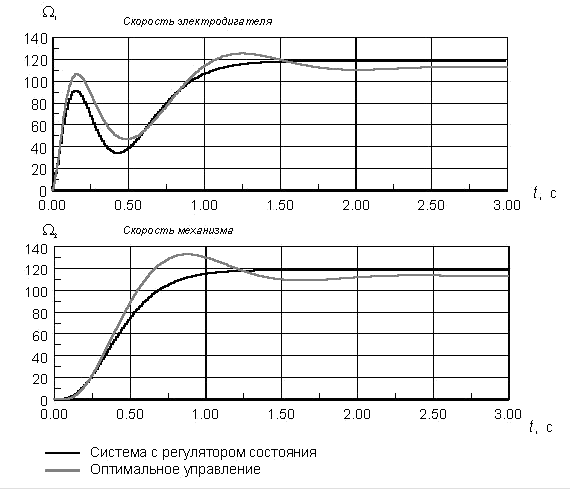
Рис. 9.2. Сравнительные динамические характеристики систем управления с регулятором состояния
Выводы
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: март 2021 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Лубенцова Е.В. Построение оптимальных систем управления. Практикум для лабораторных и практических занятий: учебное пособие / Е.В.Лубенцова – Ставрополь: Изд-во СКФУ, 2016. – 134 с.
- Попов П.М.Оптимальное управление в ходе эволюционного развития процессов и систем: Учебное пособие./Попов П.М. - Ульяновск: УлГТУ, 2000. - 148 с.
- Миллер Р. Теория переключательных схем / Р. Миллер. – М.: Наука, 1971. – Том 2: Последовательностные схемы и машины. – 304 с.
- Минский М. Вычисления и автоматы / М. Минский. – М.: Мир, 1971. – 364 с.
- Габасов Р., Кириллова Ф.М. Оптимальное управление в режиме реального времени // Вторая Международная конференция по проблемам управления. Пленарные доклады. М.: Институт проблем управления, 2003. С. 20–47.
- Албу А.В., Албу А.Ф., Зубов В.И. Вычисление градиента функционала в одной задаче оптимального управления сложной динамической системой // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 5. С. 814–833
- Васильев Ф.П., Иванов Р.П. О прибли- женном решении задачи быстродействия в банахо- вых пространствах при наличии ограничений на фа- зовые координаты // Ж. вычисл. матем. и матем. физ. 1971. Т. 11. № 2. С. 328–347.
