Назад в библиотеку

Метод конечных элементов с применением ускоренных вычислений CUDA

Авторы: Р. Е. Комаричев, С. Н. Судаков
Источник: Программная инженерия: методы и технологии разработки информационно-вычислительных систем (ПИИВС-2020): сборник научных трудов III научно-практической конференции (студенческая секция), Том 2, 25-26 ноября 2020г. – Донецк, ГОУВПО Донецкий национальный технический университет, 2020. – с. 7-10.

Аннотация

Р. Е. Комаричев, С. Н. Судаков — Метод конечных элементов с применением ускоренных вычислений CUDA. В статье проиллюстрированы основные идеи метода конечных элементов на примере простейшей краевой задачи. Расшифрована идея метода конечных элементов. Сделано указание на слабые места реализации метода конечных элементов традиционными средствами и предложены пути оптимизации, в т. ч. с применением специализированных средств CUDA. Представлены графики роста эффективности с количеством конечных элементов, а также графически продемонстрирован результат работы алгоритма.

Введение

Для анализа прочностных характеристик конструкций проводят инженерные расчёты с применением аналитических и численных методов. Аналитические методы требуют от инженера высокого уровня математической подготовки и, как правило, позволяют решать задачи только для тел с относительно простой геометрической формой. Эффективность численных методов в то же время не ограничивается ни сложностью геометрии тел, ни способами приложения сил. МКЭ (метод конечных элементов) – один из современных методов численного анализа. Широкое распространение получил после того, как объединились два его направления – инженерное и математическое [1][2].

Цель –ускорить алгоритм МКЭ с использованием средств CUDA для снижения времени обработки сложных моделей. CUDA –это архитектура параллельных вычислений, разработанная NVIDIA Corporation, которая позволяет значительно повышать вычислительную производительность с помощью графических процессоров [3].

Основная часть

Основные идеи МКЭ могут быть проиллюстрированы с помощью простейших краевых задач. Рассмотрим дифференциальное уравнение второго порядка с граничными условиями первого рода:

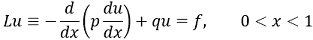(1)
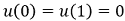(2)

Через C^k[0, 1] обозначим множество непрерывных и 𝑘 раз непрерывно дифференцируемых на отрезке [0, 1]. Через C_0^k[0, 1] — множество функций, которые также обращаются в ноль на концах отрезка [0, 1]. Примем p принадлежит C^1[0, 1], q и f принадлежат C[0, 1], причём

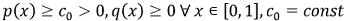(3)

Видоизменим уравнение (1), умножив его на функцию v принадлежит C_0^1[0, 1], и проинтегрируем его по отрезку [0, 1].

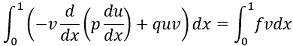(4)

Применив формулу интегрирования по частям, получим:

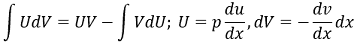(5)
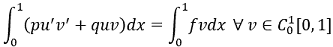(6)

Соотношение (6) является интегральным тождеством, соответствующим краевой задаче (1), (2). Если 𝑢 удовлетворяет тождеству (6), то оно есть решение задачи (1), (2), и наоборот [4].

Для приближённого решения задачи (1), (2) разобьём ось 𝑂𝑋 на 𝑛 равных частей длиной ℎ, введём множество базисных функций phi принадлежит C_0^1[0, 1], которые равны нулю на всех значениях икса, кроме областей [x_(i-1), x], где они линейно растут от 0 до 1, и [x, x_(i+1)], где линейно убывают от 1 до 0 (см. рис. 1):

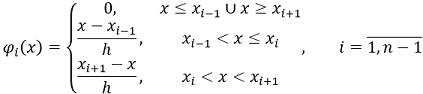(7)
Две соседние функции 𝜑(𝑥)

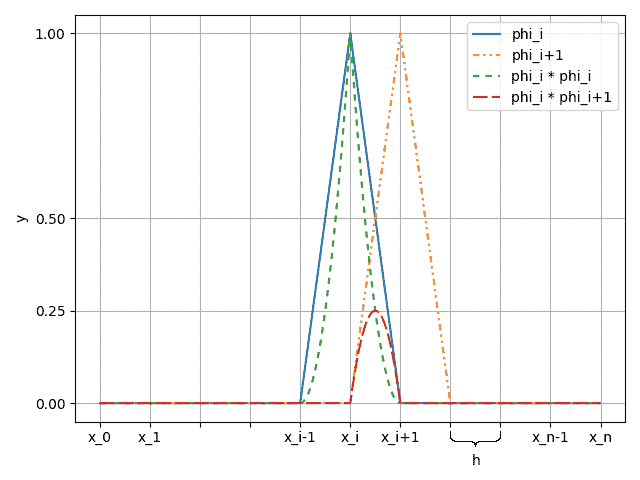
Рисунок 1 — Две соседние функции 𝜑(𝑥)

Прямая линия, полученная на каждом отрезке, есть конечный элемент. Один из примеров прикладного применения этого метода — предсказание прогиба натянутой струны, закреплённой в двух точках, под воздействием определённых сил.

Установлено, что в процессе обработки каждого конечного элемента выполняется одна и та же последовательность операций. Такая ситуация, когда требуется выполнять одинаковые инструкции снова и снова для большого количества входных данных, иначе говоря SIMD (single instruction, multiple data), является благоприятной для повышения производительности за счёт графических процессоров. Современные модели домашних центральных процессоров имеют на своём борту десятки вычислительных ядер, в то время как видеокарты — тысячи.

Даже в рассматриваемом простейшем случае задачи МКЭ выявлено несколько потенциальных участков для оптимизации. Во-первых, учитывая, что решение задачи подразумевает решение СЛАУ (системы линейных алгебраических уравнений), а количество уравнений может быть огромным, в контексте GPGPU (general-purpose computing on graphics processing units) очевидно напрашивается распараллеливание процесса формирования матрицы коэффициентов. Во-вторых, учитывая специфику МКЭ, можно быть уверенным в том, что матрица коэффициентов будет разрежённой, а именно — трёхдиагональной. Потому предлагается отказаться от привычного представления матриц в виде двумерных массивов, тем самым сэкономив не только время выполнения, а и объём потребляемой памяти. В-третьих, есть возможность выиграть на самом решении СЛАУ, возложив эту подзадачу на библиотеку cuSPARSE, которая содержит для этой цели готовые оптимизированные алгоритмы [5].

Заключение

Реализованный для ГПУ (графического процессорного устройства) алгоритм МКЭ с учётом описанных аспектов имеет для больших 𝑛 гораздо большую производительность по сравнению с версией, традиционно работающей на ЦПУ (центральном процессорном устройстве) без применения специальных средств (см. рис. 2).

Ускорения процессов заполнения матрицы коэффициентов (сверху) и решения СЛАУ (снизу) на ГПУ по сравнению с ЦПУ при различных размерах матрицы 𝑛

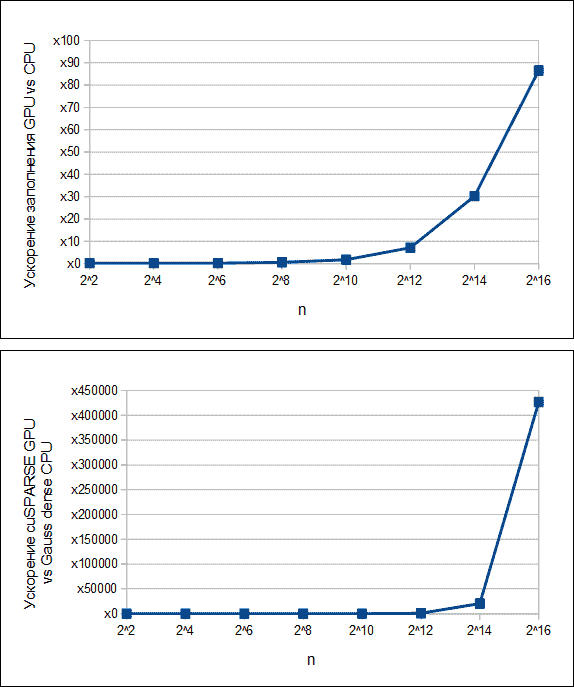
Рисунок 2 — Ускорения процессов заполнения матрицы коэффициентов (сверху) и решения СЛАУ (снизу) на ГПУ по сравнению с ЦПУ при различных размерах матрицы 𝑛

На рисунке 3 продемонстрированы графики результатов работы алгоритма для уравнений силы 𝑓(𝑥)=sin(𝑥) (сверху) и 𝑓(𝑥)=𝑥^3 (снизу) при количестве элементов 𝑛=5 (слева) и 𝑛=25 (справа). Синяя сплошная линия иллюстрирует распределение силы, оранжевый штрих-пунктир – предсказание деформации струны под воздействием этой силы.

Графики функций-результатов работы алгоритма для уравнений силы 𝑓(𝑥)=sin(𝑥) (сверху) и 𝑓(𝑥)=𝑥^3 (снизу) при количестве элементов 𝑛=5 (слева) и 𝑛=25 (справа)

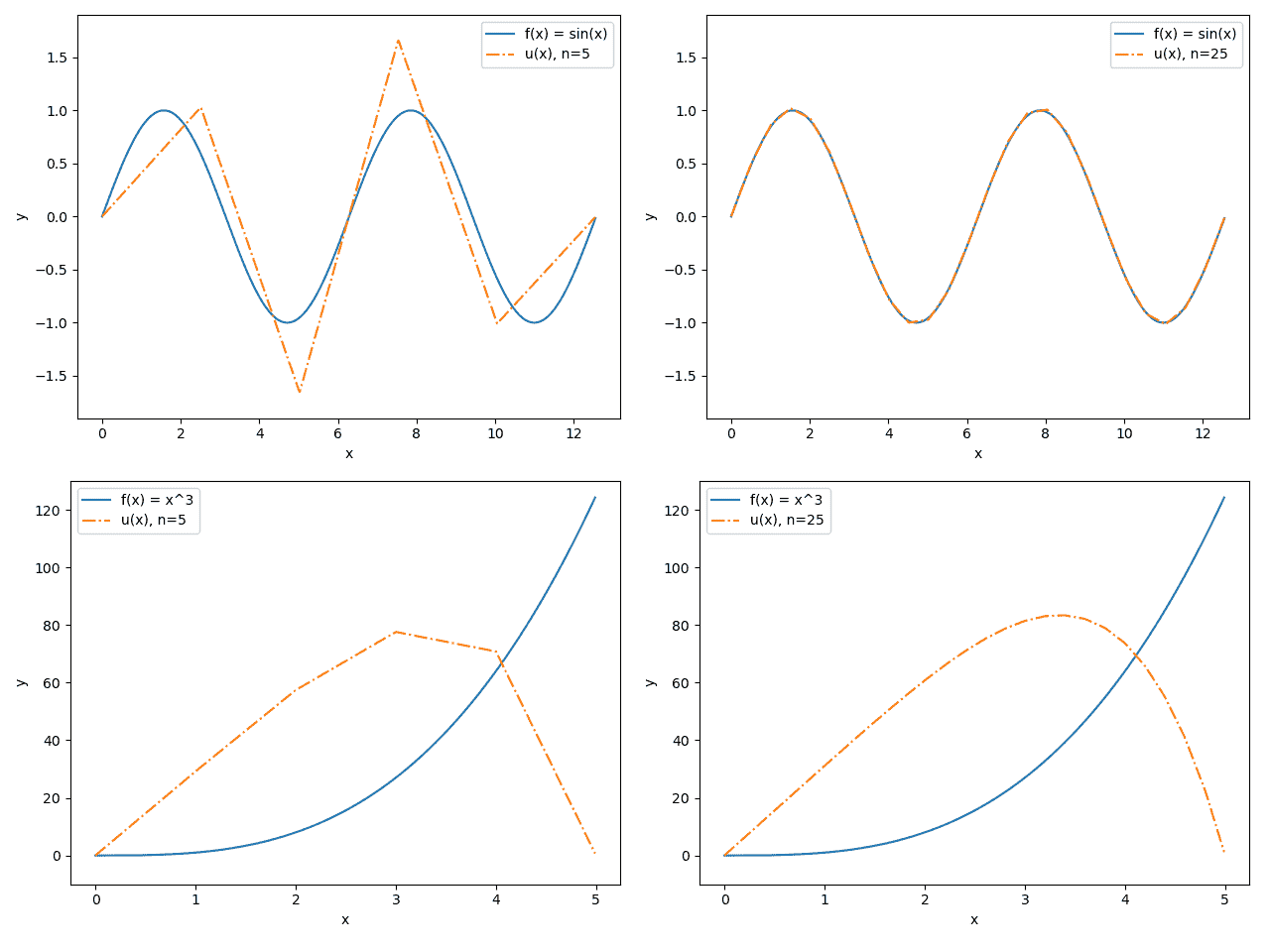
Рисунок 3 — Графики функций-результатов работы алгоритма для уравнений силы 𝑓(𝑥)=sin(𝑥) (сверху) и 𝑓(𝑥)=𝑥^3 (снизу) при количестве элементов 𝑛=5 (слева) и 𝑛=25 (справа)

Список литературы

  1. Секулович М. Метод конечных элементов / Пер. с серб. Ю. Н. Зуева; под ред. В. Ш. Барбакадзе. – М.: Стройиздат, 1993 – 664 с.: ил. – Перевод изд. Metid konacnih elemenata / Miodrag Sekulovic, 1988. – ISBN 5-274-01755-X.
  2. Стренг Г., Фикс Дж. Теория метода конечных элементов // М.: Мир, 1977-352 с.
  3. CUDA Toolkit Documentation v11.1.0 [Электронный ресурс] // CUDA Toolkit Documentation. URL: https://docs.nvidia.com/cuda/index.html (дата обращения: 06.10.2020).
  4. Даутов Р. З., Карчевский М. М. / Введение в теорию метода конечных элементов. Учебное пособие. – Казань: Казанский государственный университет им. В. И.Ульянова-Ленина, 2004. – 239с.
  5. cuSPARSE [Электронный ресурс] // CUDA Toolkit Documentation. URL: https://docs.nvidia.com/cuda/cusparse/index.html (дата обращения: 06.10.2020).
▲