Реферат по теме выпускной работы
Содержание
- ВВЕДЕНИЕ
- 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ АВТОМАТОВ
- 1.1 Планирование состояний и их переходов
- 1.2 Реализация простого конечного автомата
- 1.3 Использование конечного автомата
- 1.4 Приведенные автоматы
- 2. МИНИМИЗАЦИЯ АВТОМАТОВ
- 3. ПОСТАНОВКА ЗАДАЧИ
- 4. ПРИМЕРЫ
- ЗАКЛЮЧЕНИЕ
- Список источников
ВВЕДЕНИЕ
Теория автоматов как научная дисциплина возникла в пределах теории управляющих систем (теоретической кибернетики) в середине ХХ века, в период начавшегося бурного развития средств электронной вычислительной техники и соответствующих областей математического знания.
Потребовалась разработка теоретической базы для решения проблем, возникавших при проектировании реальных цифровых ЭВМ, а также в процессе построения и исследования гипотетических систем, таких как нейронные сети. В качестве моделей последних рассматривались конечные автоматы.
Развитие информационных технологий вывело сферу приложения теории автоматов далеко за рамки моделирования аппаратных средств цифровой электроники, расширив ее до фундаментальных основ современной теоретической информатики.
Сегодня абстракции и модели, разработанные в теории автоматов, востребованы такими научными дисциплинами как теория формальных грамматик, математическая лингвистика, теория логических моделей, математическая логика и формальные аксиоматические системы, теория кодирования, теория вычислительной сложности и другими.
Наиболее тесно теория автоматов связана с теорией алгоритмов и, в частности, с таким ее разделом как теория абстрактных машин.
В настоящее время существует ряд изданий учебного и учебно–методического назначения, в названиях которых содержится словосочетание теория автоматов
.
Нередко эти издания носят синтетический характер, объединяя под одной обложкой как элементы самой теории автоматов, так и фрагменты перечисленных выше научных областей, в которых аппарат данной теории находит мощное и вполне оправданное применение.
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ АВТОМАТОВ
Конечный автомат – это некоторая абстрактная модель, содержащая конечное число состояний чего–либо. Используется для представления и управления потоком выполнения каких–либо команд. Конечный автомат идеально подходит для реализации искусственного интеллекта в играх, получая аккуратное решение без написания громоздкого и сложного кода [1].
Конечный автомат (или попросту FSM – Finite–state machine) это модель вычислений, основанная на гипотетической машине состояний. В один момент времени только одно состояние может быть активным. Следовательно, для выполнения каких–либо действий машина должна менять свое состояние.
Конечные автоматы обычно используются для организации и представления потока выполнения чего–либо. Это особенно полезно при реализации ИИ в играх. Например, для написания мозга
врага: каждое состояние представляет собой какое–то действие (напасть, уклониться и т. д.).
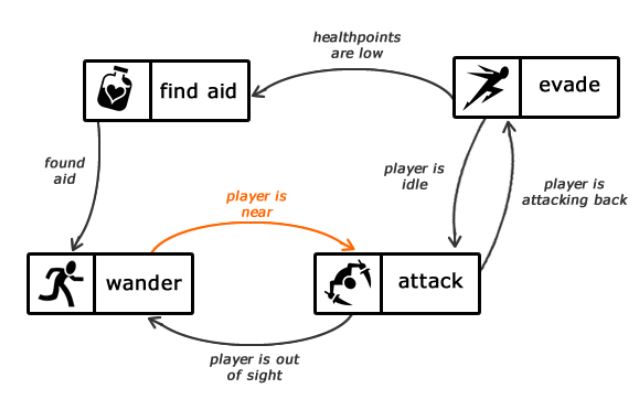
Рисунок 1.1 — Описание состояний автомата
Конечный автомат можно представить в виде графа, вершины которого являются состояниями, а ребра – переходы между ними. Каждое ребро имеет метку, информирующую о том, когда должен произойти переход. Например, на изображении выше видно, что автомат сменит состояние wander
на состояние attack
при условии, что игрок находится рядом.
1.1 Планирование состояний и их переходов
Реализация конечного автомата начинается с выявления его состояний и переходов между ними. Представьте себе конечный автомат, описывающий действия муравья, несущего листья в муравейник [2].
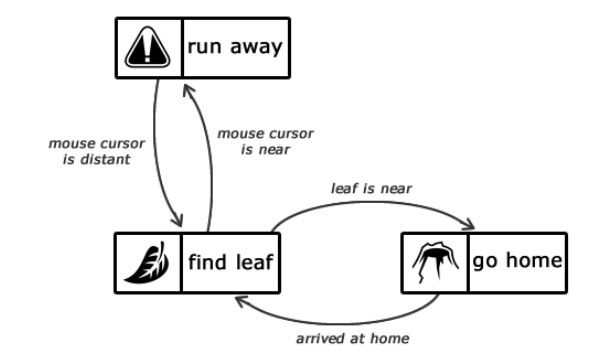
Рисунок 1.2 — Описание состояний интеллекта муравья
Отправной точкой является состояние find leaf
, которое остается активным до тех пор, пока муравей не найдет лист. Когда это произойдет, то состояние сменится на go home
. Это же состояние останется активным, пока наш муравей не доберется до муравейника. После этого состояние вновь меняется на find leaf
.
Если состояние find leaf
активно, но курсор мыши находится рядом с муравьем, то состояние меняется на run away
. Как только муравей будет в достаточно безопасном расстоянии от курсора мыши, состояние вновь сменится на find leaf
.
Нужно обратить внимание на то, что при направлении домой или из дома муравей не будет бояться курсора мыши. Почему? А потому что нет соответствующего перехода.
Стоит обратить внимание на отсутствие перехода между run away
и go home
.
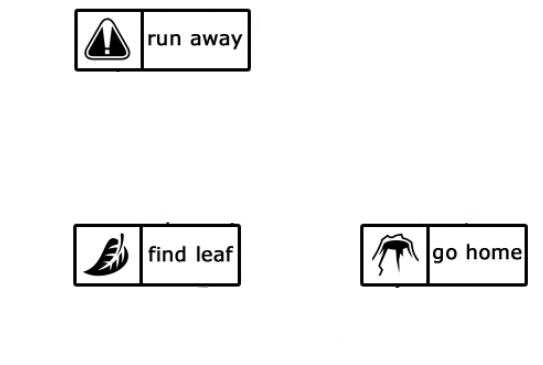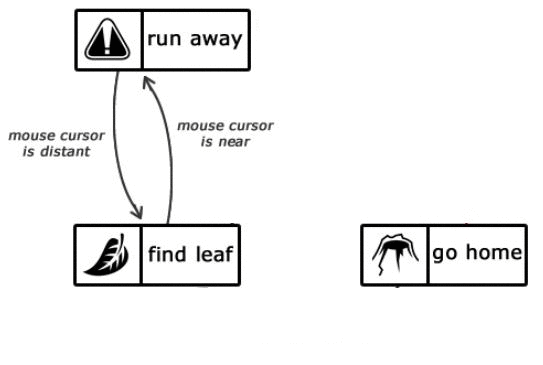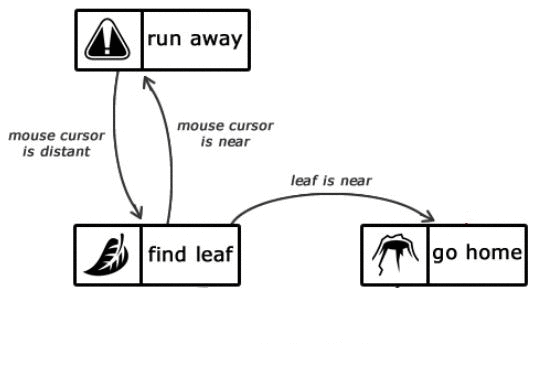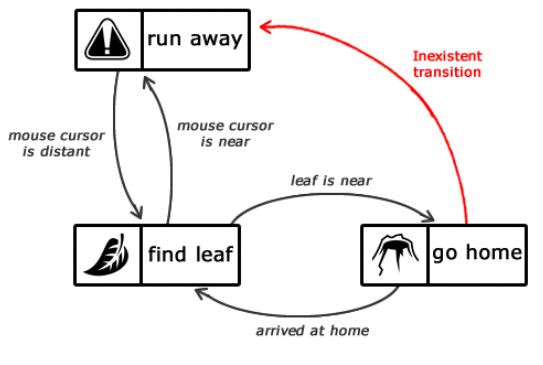
Рисунок 1.3 — Описание состояний интеллекта муравья
(анимация: 6 кадров, 6 циклов повторения, 100 килобайт)
1.2 Реализация простого конечного автомата
Конечный автомат можно реализовать при помощи одного класса. Назовем его FSM.
Идея состоит в том, чтобы реализовать каждое состояние как метод или функцию.
Также будем использовать свойство activeState для определения активного состояния.

Рисунок 1.4 — Реализация конечного автомата
Всякое состояние есть функция [3].
Причем такая, что она будет вызываться при каждом обновлении кадра игры.
Как уже говорилось, в activeState будет храниться указатель на функцию активного состояния.
Метод update() класса FSM должен вызываться каждый кадр игры.
А он, в свою очередь, будет вызывать функцию того состояния, которое в данный момент является активным.
Метод setState() будет задавать новое активное состояние.
Более того, каждая функция, определяющая какое–то состояние автомата, не обязательно должна принадлежать классу FSM — это делает наш класс более универсальным.
1.3 Использование конечного автомата
Реализуем ИИ муравья. Выше мы уже показывали набор его состояний и переходов между ними. Проиллюстрируем их еще раз, но в этот раз сосредоточимся на коде.
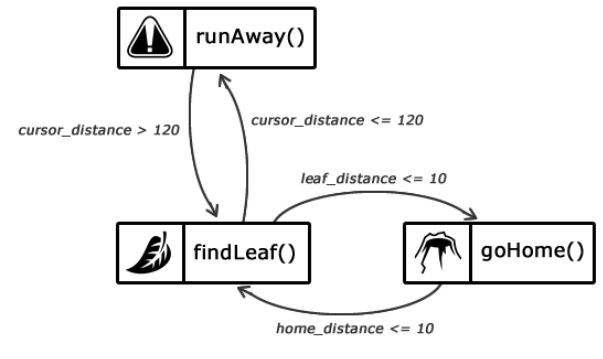
Рисунок 1.5 — Описание состояний интеллекта муравья
Наш муравей представлен классом Ant, в котором есть поле brain. Это как раз экземпляр класса FSM.
Класс Ant также содержит свойства velocity и position. Эти переменные будут использоваться для расчета движения с помощью метода Эйлера. Функция update()вызывается при каждом обновлении кадра игры.
Для понимания кода мы опустим реализацию метода moveBasedOnVelocity(). Если хотите узнать поподробнее на тему движения, прочитайте серию статей Understanding Steering Behaviors.
Ниже приводится реализация каждого из методов, начиная с findLeaf() – состояния, ответственного за поиск листьев [4].

Рисунок 1.6 — Описание состояния, ответственного за поиск листьев

Рисунок 1.7 — Состояние goHome()
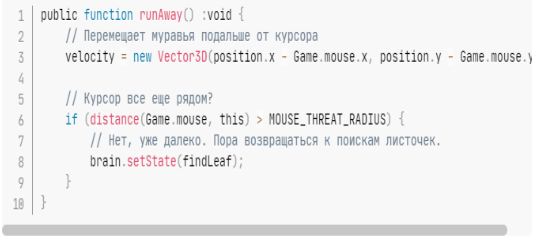
Рисунок 1.8 — Состояние runAway()
Конечные автоматы, безусловно, полезны для реализации логики искусственного интеллекта в играх.
Они могут быть легко представлены в виде графа, что позволяет разработчику увидеть все возможные варианты.
Реализация конечного автомата с функциями–состояниями является простым, но в то же время мощным методом.
Даже более сложные переплетения состояний могут быть реализованы при помощи FSM.
1.4 Приведенные автоматы
Автомат называется приведенным, если он не содержит недостижимых состояний и никакие два его состояния неэквивалентны друг другу.
Если автомат неприведенный, то можно получить эквивалентный ему автомат с меньшим числом состояний либо путем выбрасывания недостижимых состояний, либо путем объединения двух эквивалентных состояний в одно, как было показано в двух предыдущих параграфах.
Процесс приведения можно повторять до тех пор, пока не получится приведенный автомат. Таким образом, для каждого конечного автомата существует эквивалентный ему приведенный автомат.
Приведенный автомат, полученный таким способом, имеет меньшее число состояний, чем исходный (если исходный не был уже приведенным), и может быть более компактно реализован на вычислительной машине.
Осуществляя приведение различными способами или начиная с разных эквивалентных автоматов, можно предположить, что полученные приведенные автоматы окажутся разными.
Однако эти автоматы будут фактически одинаковыми во всех отношениях, за исключением имен, которыми названы их состояния.
2. МИНИМИЗАЦИЯ АВТОМАТОВ
Процесс отыскания минимальной формы называют минимизацией автомата. Полученный автомат называют минимальным. Очевидно, минимизация состоит в определении Pэкв и последующем построении характеристических функций fs, fy автомата A с учетом того, что каждый класс в Pэкв – это одно состояние A.
Таким образом, индивидуальное распознавание каждого состояния исходного автомата становится ненужным: важно только определить, к какому классу эквивалентности оно относится.
Автомат можно привести к минимальной форме различными путями. Одним из наиболее распространенных способов минимизации является итерационный алгоритм Мили. Алгоритм состоит из двух этапов, на которых осуществляется поиск пар эквивалентных состояний. Рассмотрим эти этапы.
Этап 1, шаг 1. Получение первичного разбиения.
Два состояния si и sj относим к одному классу эквивалентности ∑1h, если для каждого xk ∈ X выполняется равенство:
то есть при любом входном воздействии реакция автомата одинакова в обоих состояниях.
Этап 2, шаг (i + 1), i ≥ 1. Итерационное разбиение ранее полученных классов.
Два состояния su и sv, принадлежащие одному классу эквивалентности ∑ij (индекс i – номер шага, индекс j – номер класса), относим к классу ∑(i+1j), если для каждого xk ∈ X верно:

то есть под воздействием каждого входного сигнала автомат, находясь как в su, так и в sv переходит в состояния, принадлежащие одному и тому же классу эквивалентности ∑iw, полученному на предыдущем шаге разбиения.
3. ПОСТАНОВКА ЗАДАЧИ
Автоматы, у которых характеристические функции одинаковы, за исключением возможных различий в обозначениях состояний, называются изоморфными друг другу. Если задан автомат М, представляющий определенную систему, то любой автомат, изоморфный к М, также может служить представлением этой системы. Следовательно, представление системы автоматом ни в коем случае не единственно [7].
Если мы хотим выяснить, эквивалентны ли автоматы A1 и A2, то можно минимизировать каждый из них. Если минимальные автоматы A1' и A2' имеют множества состояний с разным числом вершин, то исходные автоматы заведомо не эквивалентны. Можно доказать, что исходные автоматы эквивалентны тогда A1' и A2' только тогда, когда соответствующие им минимальные автоматы и изоморфны. Конечные автоматы A1' и A2' считаются изоморфными, если существует такая биекция h множества состояний первого автомата на множество состояний второго, которая является изоморфизмом данных конечных автоматов как ориентированных графов и обладает дополнительно следующими свойствами:
1) если s01 – начальное состояние конечного автомата A1', то h(s01)= s02 – начальное состояние конечного автомата M2';
2) если F1 – подмножество заключительных состояний конечного автомата A1', то h(F1)= F2 – подмножество заключительных состояний конечного автомата A2';
3) для любых двух состояний s и t конечного автомата A1' и любого входного символа a имеем s → a t тогда и только тогда, когда h(s) → a h(t).
В общем случае проблема распознавания эквивалентности A1 и A2 сводится к проблеме распознавания изоморфизма минимальных автоматов. Для малого числа вершин (до 10) этот изоморфизм, как правило, распознается "невооруженным глазом", но в общем случае нужны специальные алгоритмы.
4. ПРИМЕРЫ
Прежде чем сформулировать задачу, дадим формальное определение изоморфных автоматов.
Автоматы А = (S(A), X, Y, δA, λA) и B = (S(B), X, Y, δA, λA) называются изоморфными <=> существует взаимно–однозначное соответствие φ: S(A) → S(B), сохраняющее функции переходов и выходов, то есть каждый s ∈ S(A), x ∈ X: φ(λA (s,x)) = δA (φ(s),x), λA (s, x) = λA(φ(s),x).
Постановка задачи. Для заданных автоматов А = (S, X, Y, δA, λA) и В = (S’, X, Y, δA, λA), где |S|=|S’|, найти нетривиальное множество перебросок дуг в А, в результате которых получается автомат А’, изоморфный В.
Под тривиальным множеством перебросок понимаем множество, определяемое следующим образом:
- установим произвольную биекцию: S’ → S;
- переопределим дуги в автомате А: если в автомате В имеется дуга (s’, x, y, t’), то в автомате А проводим дугу (φ(s’), x, y, φ(t’)).
Замечание. Очевидно, что для того, чтобы такие переброски были возможны, необходимо и достаточно, чтобы множества экспериментов высоты 1 у автоматов А и В совпадали, то есть WA^1 = WB^1.
Рассмотрим несколько примеров построения искомых перебросок дуг.
Пример 1.
Пусть автоматы А и В представлены на рис. 4.1 и 4.2.
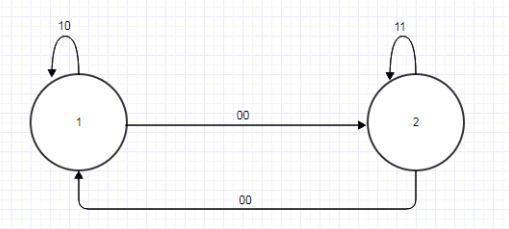
Рисунок 4.1 — Граф автомата А
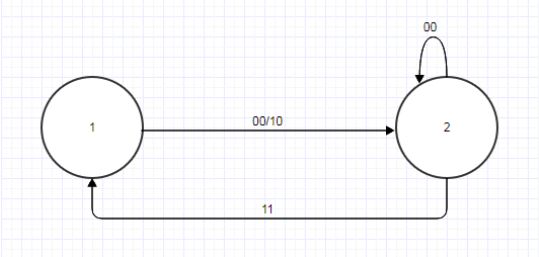
Рисунок 4.2 — Граф автомата B
Заметим, что множества экспериментов высоты 1 у автоматов А и В совпадают: WA^1 = {{00,10}, {01,10}} = WB^1.
Очевидно, что в результате переброски состояние 1 в А’ должно быть эквивалентно состоянию 1’ в В, а состояние 2 в А’ – состоянию 2’ в В.
Очевидно, что для этого необходимо перебросить три дуги:
- (1, 1, 0, 1) заменяем дугой (1, 1, 0, 2) (переброска дуги в состояние 2;
- (2, 1, 1, 2) – (2, 1, 1, 1) (переброска в состояние 1);
- (2, 0, 0, 1) – (2, 0, 0, 2) (переброска в состояние 2).
Результат переброски изображен на рис. 4.3.
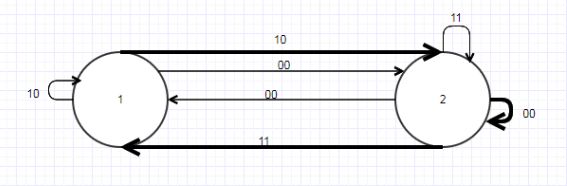
Рисунок 4.3 — Автомат А’
В результате переброски должен быть получен автомат А’ изоморфный В. Изоморфизм автоматов может быть проверен с помощью алгоритма Рк–таблиц (см. Гилл) для автомата, который получается приписыванием к автомату В автомата А’. Обозначим полученный автомат А’uВ.
Рассмотрим последовательный процесс построения Рк – таблиц для автомата А’uВ. В процессе построения Рк – таблиц любая такая таблица должна обладать следующим свойством:
(*) Каждый её класс эквивалентности должен содержать одинаковое число состояний как автомата А’, так и В.
В силу равенства WA^1=WB^1 каждый класс таблицы Р1 обладает этим свойством. На следующем шаге, в таблице Р2, это свойство может быть нарушено. Чтобы не допустить такого нарушения нужно организовать переброску некоторых дуг. Рассмотрим данный процесс на примерах.
Пример 2.
Рассмотрим два автомата А и В, показанные на рисунках 4.4 и 4.5:
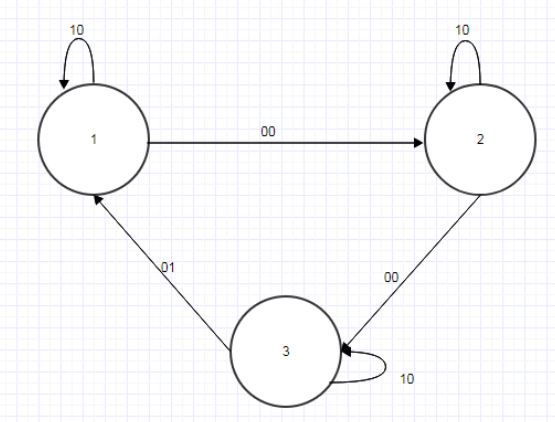
Рисунок 4.4 — Граф автомата А
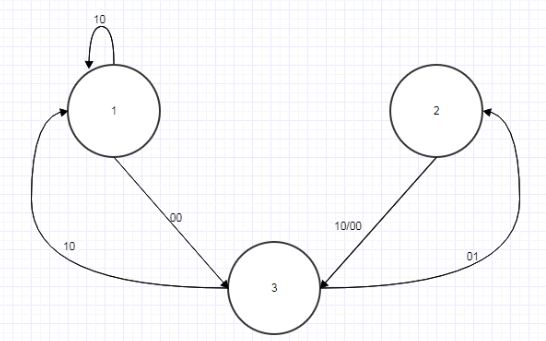
Рисунок 4.5 — Граф автомата B
Строим Рк–таблицы для А’uB (табл. 4.1, 4.2):
Таблица 4.1 — Р2.
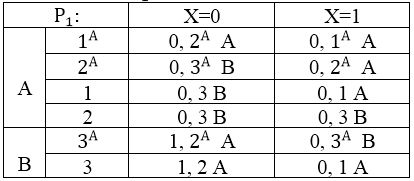
Из таблицы Р1 видно, что:
- Класс В в следующей таблице Р2 распадется на два подкласса: {3}, {3^А}. Для недопущения этого необходимо дугу (3^А,1,0,3^А) перебросить в состояние, которое окажется эквивалентным состоянию 1 в автомате В, то есть в состояние φ(1).
- Класс А в следующей таблице Р2 распадется на три подкласса: {1^А}, {2^А,1}, {2}. При этом свойство (*) будет нарушено из–за классов {1^А} и {2}. Для предотвращения этого нарушения нужно объединить состояния 1^А и 2 в Р2. Это можно сделать переброской двух дуг: заменой (1^А, 0, 0, 2^А) на (1^А, 0, 0, φ(3)) и (1^А, 1, 0, 1^А) на (1^А, 1, 0, φ(3)).
Таблица 4.2 — Р2.
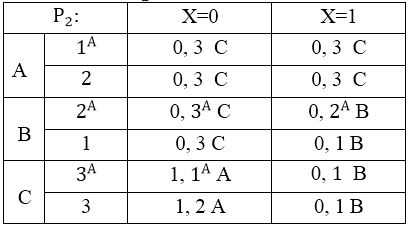
Из таблицы Р2 видно, что автомат А’ изоморфен В, так как каждый класс содержит по одному состоянию из А’ и В.
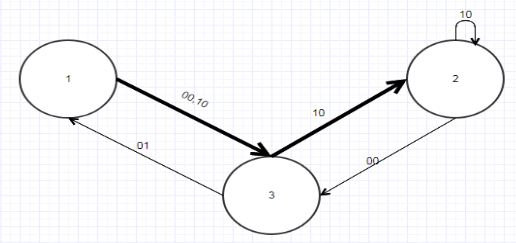
Рисунок 4.6 — Граф автомата А’
Пример 3.
Пусть автоматы А и В представлены на рис. 4.7 и 4.8.
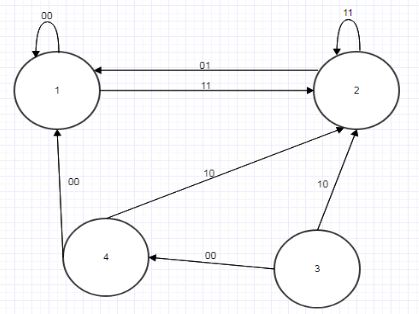
Рисунок 4.7 — Граф автомата А
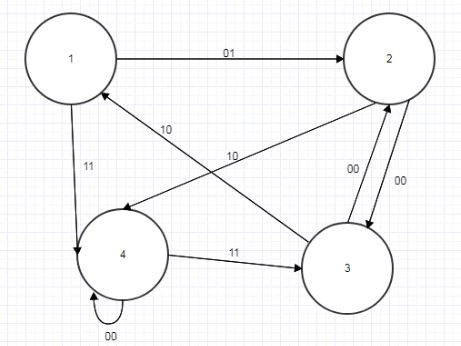
Рисунок 4.8 — Граф автомата В
Строим Рк-таблицы для А’uB (табл. 4.3, 4.4):
Таблица 4.3 — Р2.
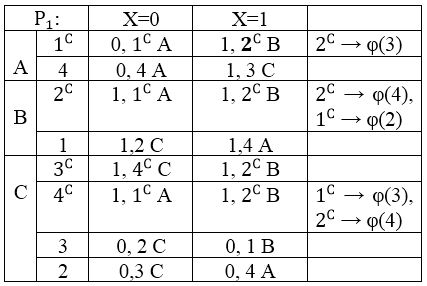
Из таблицы Р1 видно, что:
- Класс А в следующей таблице Р2 распадется на два подкласса: {4}, {1C}. Для недопущения этого необходимо дугу (1C,1,1,2C) перебросить в состояние, которое окажется эквивалентным состоянию 3 в автомате В, то есть в состояние φ(3).
- Класс В в следующей таблице Р2 распадется на два подкласса: {1}, {2C}. Для недопущения этого необходимо дугу (2C,0,1,1C) перебросить в состояние, которое окажется эквивалентным состоянию 2 в автомате В, то есть в состояние φ(2). Кроме того дугу (2C,1,1,2C) необходимо перебросить в состояние, которое окажется эквивалентным состоянию 4 в автомате В, то есть в состояние φ(4).
- Класс С в Р1 удовлетворяет условию *, но это условие будет нарушено в таблице Р2. Заметим, что состояние из класса С можно группировать по разному для сохранения условия * в Р2. Поскольку состояния 3C и 3 2-эквивалентны, то осталось сохранить 2-эквивалентность состояний 4C и 2. Для этого необходимо выполнить переброску дуги (4C, 0, 1, 1C) в состояние φ(3), а также дуги (4C, 1, 1, 2C) в состояние φ(4).
Таблица 4.4 — Р2.
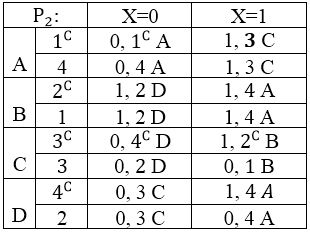
Из таблицы Р2 видно, что автомат А’ изоморфен В, так как каждый класс содержит по одному состоянию из А’ и В (рис. 4.9).
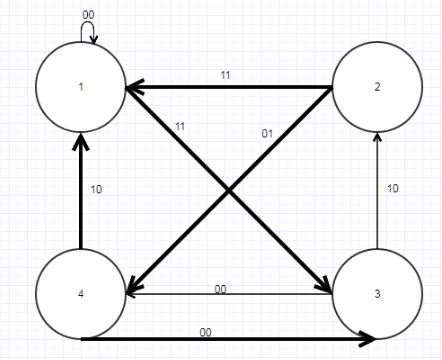
Рисунок 4.9 — Граф автомата А’
Заключение
В рамках данной работы был проведен ряд экспериментов с автоматами, которые позволяют сформулировать процедуру порождения одного автомата из другого. Данная процедура состоит в построении Рк–таблиц для автомата А’UB и переопределении перебрасываемых дуг в А’ таким образом, чтобы в процессе переброски каждый класс каждой Рк–таблицы состоял из одинакового числа состояний автомата А’ и автомата В.
Данная процедура обладает свойством недетерминизма и в последующем будет представлена в виде алгоритма.
Список источников
- Брауэр, В. Введение в теорию конечных автоматов / [пер. с нем]. – М.: Радио и связь, 1987. – 392 с.
- Гуренко, В. В. Введение в теорию автоматов / В. В. Гуренко – Москва: МГТУ им. Н. Э. Баумана, 2013. – С. 4–19.
- Капитонова, Ю. В. Основы дискретной математики / Ю. В. Капитонова, С. Л. Кривий, А. А. Летичевский, Г. М. Луцкий, Н. К. Печурин. – К.: Наукова думка, 2002. – 568 с.
- Ковалев Д. В., Копытова О. М. Разработка и исследование метода построения функции деградации поведения конечного автомата в результате переброски дуг // Сборник материалов II Международной научно–практической конференции
Программная инженерия: методы и технологии разработки информационно–вычислительных систем
(ПИИВС–2018). – Донецк: ДонНТУ, 2018. – С. 230 – 233. - Буевич, В. А. Автомат конечный / В. А. Буевич [Электронный ресурс]. – Режим доступа: https://scanwordbase.ru/vocabulary...
- Горяйнова, Анастасия Вячеславовна Разработка и исследование метода анализа групповых автоматов, полученных переброской дуг в эталоне. – [электронный ресурс]. – http://masters.donntu.ru/2017/fknt/...
- Минимизация конечных автоматов [Электронный ресурс]. – http://mathhelpplanet.com/static...
- Изоморфизм и эквивалентность автоматов [Электронный ресурс]. – https://studfile.net/preview...
- Изоморфные автоматы [Электронный ресурс]. – https://studopedia.ru/5...
