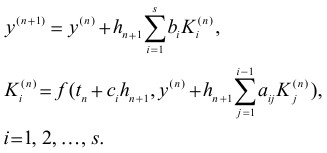
Авторы: Г.В. Ващенко, Е.А. Новиков
Источник:// Вестник КрасГАУ. 2010. №2. – С. 14-18.
Ключевые слова: явные методы Рунге-Кутта, параллельные алгоритмы, кластеры, полный граф.
Рассматривается задача Коши для систем обыкновенных дифференциальных уравнений первого порядка
y'= f (t, y), y (t0) = y0. (1)
Для численного решения задачи (1) применяются явные s-стадийные методы типа Рунге-Кутта, (n+1)-й шаг в которых задается формулами (2)
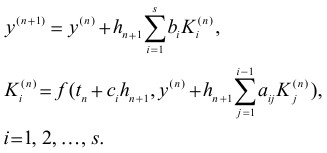
Конкретный метод Рунге–Кутта описывается набором коэффициентов bi, ci, aij, 1 ≤ i ≤ s, 2 ≤ j ≤ (i–1) [2, 3, 4].
Здесь представлены параллельные вычислительные схемы для s-стадийных явных методов типа Рунге-Кутта и параллельные алгоритмы, ориентированные на применение в многопроцессорных вычисли- тельных системах кластерной архитектуры. Основной подход при конструировании параллельных методов состоял в распараллеливании последовательных численных алгоритмов, использовании декомпозиции на подзадачи [1; 5] исходной задачи (2) и анализе информационных взаимосвязей между ними. Поиск макси- мально возможного независимого набора операций с целью их распараллеливания осуществлялся путем построения графов зависимостей. Суть построения графов заключается в сопоставлении вершинам графа выполняемых независимо операций, а дугам – результата влияния выполнения операции на результат неко- торых соседних операций.
В данной работе будем отталкиваться от неоднократно апробированных последовательных алгоритмов решения задачи (1) методами (2). Рассмотрим последовательную вычислительную схему. Для определенности зададимся некоторым отрезком [t0, T] и введем равномерную сетку wn=(t0, t1,..., tn) с величиной шага hn+1=h. На сетке wn в начальный момент времени t0 в качестве начального условия зададим вектор y(0) (y1(0), y2(0), ..., yN(0)). Тогда построение численного решения сводится к нахождению последовательности значений y~(0), y~(1), ..., y~(n), являющихся приближением значений y(t0), y(t1), y(t2), y(tn) точного решения y(t) в узлах сетки wn.

Как видно из (2) и (3), определение значения y~(n+1) сводится к строго последовательному вычислению коэффициентов K1(n), K2(n), Ks(n), их умножению на коэффициенты bi, i=1, 2, ..., s соответственно и последующему суммированию. Исходя из формулы (3), последовательный алгоритм в общем случае построения численного реше- ния задачи (1) может быть представлен в виде:
начало;
ввод начального вектора y0;
вычисление шага h;
цикл по числу узлов сетки n = 1, 2, ..., М - 1;
цикл по числу стадий m = 1, 2, ..., s;
цикл по числу компонент i = 1, 2, ..., N;
вычисление коэффициентов Kmn, i(n);
конец цикла по i;
конец цикла по m;
цикл по числу компонент j = 1, 2, ..., N;
вычисление yj(n+1) ;
конец цикла по j;
цикл по числу компонент j = 1, 2, ..., N;
сохранение, yj(n)= yj(n+1);
конец цикла по j;
вывод y(n+1) ;
конец цикла по n;
конец.
Заметим, что этот алгоритм может видоизменяться, например, при организации вычислений с контролем точности и устойчивости, с управлением величиной шага и другими возможными условиями, исходящими от типа решаемой задачи и требований, предъявляемым к численному решению. Однако строго последовательный характер вычисления коэффициентов K1(n), K2(n), ..., Ks(n) останется неизменным.
Практическая реализация вычислений по приведенному обобщенному алгоритму зависит от системы программирования, способу организации вычислений правой части системы (1), способу формирования числовых массивов и доступа к их элементам.
Для разработки параллельной схемы решения задачи (1) явными методами (2) заметим, что последовательная схема (3) дает основание организации двух типов параллельных вычислений:
а) вычисление отдельных компонент коэффициентов K1(n), K2(n), ..., Ks(n) и вектора численного решения y~(n+1) = (y1~(n+1), y2~(n+1), yN~(n+1);
б) вычисление отдельных операций внутри одного шага метода.
Следует отметить, что вычисление отдельных операций внутри одного шага метода обеспечивает небольшую степень параллелизма и поэтому рассматриваться не будет.
Анализ формулы (3) показывает, что вычисление любой компоненты вектора приближенного решения y~(n+1) в каждом узле сетки wn сводится к вычислению произведения коэффициента bm на компоненты Km, l, m = 1, 2, ..., s; l = 1, 2, ..., N и последующему суммированию результатов умножения b1K1, l + b2K2,l + ... + bsKs,l . В силу этого, за базовую подзадачу примем вычисления компонент Km, l, m = 1, 2, ..., s; l = 1, 2, ..., N.
Введем в рассмотрение вектор
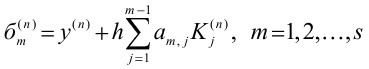
с элементами (4)

тогда коэффициенты Km, l(n) будут определяться формулой (5)
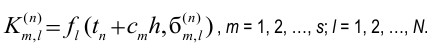
Теперь построим общую параллельную схему вычислений. Рассмотрим информационные зависимости, возникающие при вычислении коэффициентов Km, l(n), m = 1, 2, ...,s, l = 1, 2, ..., N, при получении вектора y~(n+1). Будем предполагать, что имеется N (p = N) компьютеров (рис.1), на каждом из которых вычисляется последовательно один коэффициент Km, l(n) по формуле (5) и элемент бm, l(n), m = 1, 2, ..., s, l = 1, 2, ..., N по формуле (4). В системе каждый компьютер связан с каждым, то есть имеем полностью связанную систему. Тогда процесс вычислений организуется согласно рис. 2.
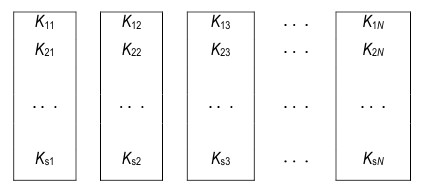
Рис. 1. Схема параллельной вычислительной системы
Шаг 1. Вычислить K1, i и delta2, j по формулам
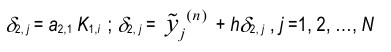
и переслать K1, i и alfa2, j всем N – 1 компьютеру.
Шаг 2. Вычислить K2, i и alfa3, j по формулам
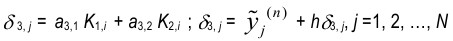
и переслать K2, i и delta3, j всем N – 1 компьютеру.
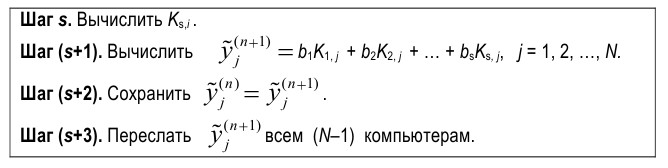
Рис. 2. Вычисление коэффициентов и вектора приближенного решения при p = N
На последнем шаге в каждом компьютере вычисляется и сохраняется j-я компонента вектора y~(n+1). Число пересылок для расчета в одном узле сетки wn составит s(N – 1)2 ≈ O(sN 2). При высокой размерности исходной задачи (1) затраты на пересылку являются определяющими для времени решения (1). Сокращение затрат в общем случае можно уменьшить только укрупнением схемы параллельных вычислений, то есть за счет увеличения числа коэффициентов, вычисляемых на одном компьютере. Рассмотрим в качестве примера схему, которая показана на рис.3. Здесь для определенности размерность N кратна числу p, то есть N = kp. В каждом компьютере размещено и вычисляется последовательно по k компонент векторов коэффициентов, K1(n), K2(n), ..., Ks(n). Вычисления реализуются по правилу, показанному на рис. 4.

Рис. 3. Укрупненная схема параллельной вычислительной системы
Шаг 1. Вычислить K1, lz (n) и б2, lz (n) по формулам
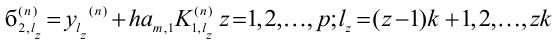
и переслать K1, lz (n) и б2, lz (n) всем (p-1) компьютерам.
Шаг 2. Вычислить K2, lz (n) и б3, lz (n) по формулам
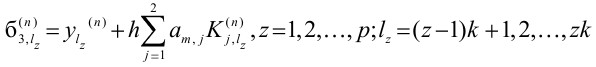
и переслать K2, lz (n) и б3, lz (n) всем (p-1) компьютерам.

Рис. 4. Вычисление коэффициентов и вектора приближенного решения при N = kp
На последнем шаге в каждом компьютере вычисляется и сохраняется своя часть вектора y~(n+1) . Таким образом, после параллельного вычисления коэффициентов параллельно определяется такое же количество компонент вектора приближенного решения y~(n+1) . Число пересылок для одного узла сетки wn составит s(p–1)2 O(sp2). Заметим, что в отдельных случаях, зависящих от типа и вида исходной системы (1), может быть достигнута максимальная степень параллелизма и соответственно сокращение временных затрат выполнения вычислений по разработанному алгоритму.
Рассмотренные параллельные схемы явных методов типа Рунге-Кутта ориентированы на реализацию в многопроцессорных вычислительных системах кластерной архитектуры с использованием технологии MPI. MPI имеет в составе коммуникационные операции, попарные и коллективные обмены, средства организации виртуальных топологий. Как показали исследования представленных параллельных схем, для их реализация наиболее подходящими могут быть такие топологии, как кольцо, линейка, решетка и гиперкуб.
Разработанные схемы могут служить основой для разработки параллельных алгоритмов решения задачи Коши явными методами с контролем точности и устойчивости, алгоритмов переменного порядка и шага, а также возможной автоматизации построения методов интегрирования с адаптивной областью устойчивости.