История создания теории групп

Аннотация

Цвиркун А. Е. История создания теории групп. Рассмотрена тема создания и становления теории групп как самостоятельного раздела математики. Собраны наиболее интересные факты для более полного представления об истории теории групп. Рассмотрена нынешняя ситуации в этой области и приложениях теории групп в различных областях математики, дизайна, геометрии и физики.

Annotation

Tsvirkun A. E. The history of the creation of group theory. The topic of the creation and formation of group theory as an independent branch of mathematics is considered. Collected the most interesting facts for a more complete understanding of the history of group theory. The current situation in this area and applications of group theory in various areas of mathematics, design, geometry and physics are considered.

Общая постановка проблемы

Математика играет довольно весомую роль в жизни современного общества и находит широкое применение при решении самых разнообразных задач науки и практики.

Одной из наиболее важных и быстро развивающихся областей современной математики является абстрактная алгебра, в центре внимания которой сейчас находятся различные алгебраические структуры, такие, как группы, подгруппы, полугруппы, кольца и так далее, ставшие уже классическими. Группы, по существу, являются один из основных типов алгебраических структур.

В качестве самостоятельного раздела математики теория групп начала формироваться в конце XVIII века. До 1830 года она развивалась медленно и практически не привлекала к себе внимания. Но благодаря работам Галуа и Абеля всего за несколько лет она совершила гигантский скачок, который оказал глубокое влияние на развитие всей математики. С тех пор стали детально исследоваться и основные понятия теории групп.

В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей применения, как в самой математике, так и в физике.

Цель исследования

Рассказать об истории создания теории групп, процессе её исторического развития и её приложениях в физике, геометрии и дизайне.

Исследования

Многие ученые склонны верить сейчас, что в действительности понятие группы является древнейшим математическим понятием, даже более древним, чем понятие числа, и неотделимым от самой человеческой цивилизации. Группы существуют всюду, где возникает симметрия, например, такие повторяющиеся и самовоспроизводящиеся узоры как орнамент. Они давно присутствует в архитектуре стран Ближнего востока и Азии.

Официально теория групп выделилась как самостоятельная наука в начале XIX века.

У теории групп три исторических корня: теория алгебраических уравнений, теория чисел и геометрия. Математики, стоящие у истоков теории групп, – это Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, Нильс Хенрик Абель и Эварист Галуа.

К концу XVIII века алгебра была уже не просто искусством вычислений с числами, буквами и другими величинами, содержащими несколько правил, несколько формул и умением как-то правильно их толковать [1]. Комплексные числа были уже всеми почти признаны, существовала некоторая теория линейных уравнений, уже намечались подходы к исследованию уравнений произвольной степени от одного неизвестного, но рядом с успехами математического анализа это было очень и очень мало.

С XVI века одной из главных задач алгебры стала задача решения алгебраических уравнений в радикалах. И алгебру тогда называли наукой о решении уравнений. Более точно в ней ставилась задача: найти способы выражать корни уравнений Уравнение имеет следующий вид:

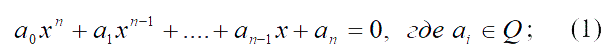
через коэффициенты уравнения с помощью четырех арифметических операций и операций извлечения арифметического корня произвольной степени. К этому моменту умели решать в радикалах уравнения квадратные, кубические (метод Джероламо Кардана, Николо Тартальи) и четвертой степени (метод Луиджи Феррари).

В поисках общей формулы математики перепробовали громадное количество методов, но все они оказались безрезультатными, и начала нарастать уверенность, что в общем случае задача решения не имеет. Конечно, большим триумфом было бы найти методы решения уравнений произвольной степени с произвольными коэффициентами, впрочем, бессчетные поиски такого метода не имели успеха.

Как отмечается в книге Колмогорова [1] до 1770 года не было даже известно, как решать в радикалах уравнение вида: xⁿ - 1 = 0 при n > 10.

Успехи достигнуты были только в XIX веке благодаря результатам Гаусса, Абеля и Галуа. Ими было показано, что разрешимости уравнения (1) в радикалах в общем случае нет.

В решении этой задачи большую роль сыграла группа подстановок – группа из всех возможных перестановок n элементов, изменяющих порядок их следования. С её помощью было показано, что коэффициенты многочлена (1) должны быть симметричными функциями его корней. И этого оказалось нельзя добиться с помощью применения арифметических операций и радикалов для выражения корней через коэффициенты уравнения (1).

Введение понятия группы было большим достижением, но не общеприменимым для решения других задач, так как в первой половине XIX века теория групп была, в основном, еще теорией группы подстановок и её подгрупп. Что понятие группы имеет более обширное применение, выяснилось уже к середине века. Заметный вклад в развитие её теории внесли математики Огюстен Луи Коши и Артур Кэли. Кэли первым сформулировал определение группы, применяемое и сегодня, как множества с бинарной операцией ×, подчиняющейся определённым условиям. Процесс перехода к абстрактной теории групп заметно ускорился только после 1870 года, когда её начали излагать в лекциях по алгебре в Сорбонне. Успех её развития связан с именами Жордана, Бертрана, Эрмита, Фробениуса, Кронекера и Матьё.

К XIX веку господствовало представление А. Кэли, Ф. Клейна и С. Ли по определению группы, как такой совокупности однозначных операций {e,a,b,...,x,y,z}, что комбинация двух любых её операций, a, b, дает, например, операцию c из той же совокупности, a×b = c.

В настоящий момент, формально определение выглядит следующим образом [2-5]. Группа G – это множество с бинарной операцией ×, подчиняющейся следующим аксиомам:

1. для ∀x,y ∈ G выполняется x × y = z∈ G (замкнутость);
2. для ∀x,y ∈ G выполняется (x × y) ×z = x × (y × z) (ассоциативность);
3. существование единицы: e ∈ G и для ∀x ∈ G выполняется x × e = e × x = x;
4. для ∀x ∈ G существует ему обратный элемент x^-1 ∈ G, такой что выполняется тождество x × x^-1 = x^-1 × x = e.

При изучении структуры групп с небольшим числом её элементов, для которых верны аксиомы группы G удобно применение таблицы умножения её элементов. По определению группы у неё один единичный элемент, у каждого элемента есть обратный, и в результате применения бинарной операции, умножения любого элемента группы на все её элементы ни один элемент не появится дважды. Рассмотрим пример группы из 4-х элементов, {e, a, b, с}. Для неё можно построить три разные таблицы умножения, то есть она имеет три структуры.

Таблица 1 – Возможные структуры, G1, G2, G3, группы {e, a, b, с}.

Мы получаем циклическую группу G3, все элементы которой получаются как степени одного элемента симметрии a: b = a², c = a³, e = a⁴. У этой группы есть инвариантная подгруппа из элементов {e,b} ∈ G₃, которая коммутирует со всеми элементами группы G3 и поэтому является её нормальной подгруппой. Группы, у которых все элементы коммутируют называют абелевыми, группы G1, G2, G3 – абелевые. Группа G3 изоморфна, группе вращений четырёхугольной пирамиды вокруг её оси симметрии. Для неё все вращения появляются, как степени поворота на 90 градусов. Изоморфизм – это взаимооднозначное соответствие между элементами сравниваемых групп с точностью до бинарной операции [2-5]. Группа G2 имеет нормальную подгруппу {e,a} ∈ G₂. Она изоморфна группе симметрии правильной 4-х угольной призмы, у которой основания раскрашены одинаковыми линиями, но под углом 90° друг к другу. Группа G1 имеет три нормальные подгруппы, {e,a},{e,b},{e,c}∈ G₁, и изоморфна группе отражений в трёх плоскостях декартовой системы координат.

Теорию абелевых групп успешно развивали Г. Фробениус и Л. Штикельберг [6, 7].

К концу XIX века Софус Ли уже изучал бесконечные непрерывные группы. Их сейчас называют группами Ли. За ним последовали работы Киллинга, Штуди, Шура, Маурера и Эли Картана. Бесконечные дискретные группы исследовали Клейн, Ли, Пуанкаре и Пикар.

К этому времени по теории конечных групп уже появилась учебная литература, что способствовало и появлению первых приложений теории групп, оказавших большое влияние и на физику, в частности, на теорию электромагнитного поля, группа Лоренца. В то же время трудами ученых Фёдорова, Шенфлиса, Клейна дискретные группы нашли широкое применение в кристаллографии для классификации кристаллических структур.

К концу XIX и первым десятилетиям XX века теория конечных групп достигла своего расцвета благодаря трудам своих крупнейших деятелей (Фробениус, Гельдер, Бернсайд, Шур, Миллер) и в законченном виде дошла до наших дней. В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные приложения как в самой математике, так и за ее пределами – в топологии, в теории функций, в кристаллографии, в квантовой механике и в других областях математики и естествознания. Среди основных результатов, нашедших применение в квантовой теории стоит отметить теорию представлений групп (гомоморфизмы на матрицы), леммы Шура, устанавливающей ортогональность базисных функций неприводимых представлений групп и разложения приводимых представлений и неприводимые. В качестве гомоморфных групп в теории представлений берут группы, элементы которых матрицы, а бинарная операция – матричное умножение. В квантовой теории многоэлектронных систем широкое применение нашли точечные группы (с операциями симметрии вращения, отражения и инверсии), группы трансляций (параллельных переносов) и группы перестановок, позволяющей правильно учитывать неразличимость электронов и принцип Паули в антисимметричной волновой многоэлектронной функции. Их применение упрощает решение задач на собственные значения для приближённых методов решения уравнения Шредингера. А непрерывные группы унитарных вращений оказались применимыми и в теории элементарных частиц для их классификации. Эти результаты получены Юнгом, Яманучи, Рака, Вигнер [2-6]. Без этих достижений невозможно представить современное развитие теории атомов и молекул, твердого тела, ядерной физики элементарных частиц и теории поля.

Во многом, эти успехи стали результатом того, что в теории групп, как разделе математики поняли, что конечность групп является слишком сильным и не всегда естественным ограничением, очень скоро, которое привело к конфликту с потребностями соседних отделов математики: различных частей геометрии, теории автоморфных функций, топологии, где все чаще и чаще стали встречаться подобные группам, но бесконечные алгебраические образования. Они стали предъявлять к теории групп требования, которые теория конечных групп была не в состоянии удовлетворять.

Впервые в мировой литературе изложение основ теории групп без предположения, что рассматриваемые группы конечны, было cделано в книге О. Ю. Шмидта Абстрактная теория групп (1933 год) [8]. Однако, широкое развитие общей теории групп началось несколько позже и было связано с радикальной её перестройкой и переходом в математике на теоретико-множественные основы, которые алгебра совершила в 20-х годах нашего века (Э. Нётер). Именно после этого пришли в теорию групп такие новые для нее понятия, как системы операторов, условия обрыва цепочек и другое.

В дальнейшем, после преобразований, работа в общей теории групп становилась все более бурной и разносторонней и сейчас эта часть математики превратилась в широкую и богатую содержанием науку, занимающую одно из первых мест в современной алгебре [6].

Теория групп принесла свои новые способы решения задач в ряд математических дисциплин. Например, в алгебраическую топологию с фундаментальными группами в ней. Можно, кроме топологии, упомянуть и различные комбинаторные задачи, целочисленное программирование и математической моделирование.

Теория групп также оказала неоценимую помощь при решении задач классификации в различных областях прикладной математики, оказала влияние на развитие теории инвариантов, поиск общих решений дифференциальных уравнений и так далее.

Также теория групп способствовала появлению новых областей в математике. Например, алгебраическая теория чисел, теория колец, полей. Во многом благодаря теории групп, современная алгебра теперь такая, какой мы её знаем, и не уступает анализу.

Каждый год проходят международные конференции, посвященные теории конечных и бесконечных групп. В частности, в России это направление развивается достаточно активно. Хорошо развитые школы, занимающиеся теорией групп, имеются в Москве, Санкт-Петербурге, Екатеринбурге, Новосибирске, Омске, Томске, Иркутске, Челябинске, Красноярске и других городах России. Сотни специалистов высшей квалификации занимаются различными разделами теории групп. В России регулярно выходят журналы Алгебра и логика, Сибирский математический журнал, Фундаментальная и прикладная математика, Дискретная математика, Доклады академии наук. В них большую долю занимают статьи по теории групп. Российскими учеными написаны десятки монографий по конечным и бесконечным группам. Достижения российских специалистов по теории групп давно и заслуженно признаны во всем мире.

Продолжает развиваться и теория конечных групп. Одним из больших успехов этой, старейшей и, в то же время, наиболее активно развивающейся ветви теории групп. явилось завершение классификации конечных простых групп, включая серии групп алгебраического типа, знакопеременные группы An, – знакопостоянные подгруппы группы перестановок, а также спорадических простых групп, среди которых наибольшая группа Большой Монстр имеет порядок, 2⁴⁶× 3³⁰× 5⁹× 7⁶× 11²× 13³× 17× 19× 23× 29× 31× 41× 47× 59× 71, что около 1054. Её называют Бэби Монстром [7].

Исключительная роль простых конечных групп объясняется тем, что из них может быть построена любая конечная группа. Серьезно изучены конечные разрешимые группы по свойствам различных систем подгрупп (силовских, холловских, картеровских и др.) Можно отметить теорему У. Фейта (W. Feit) и Дж. Томпсона (J. Thompson) 1963, о том, что все конечные группы нечетного порядка разрешимы [7]. Теория групп подстановок и теория линейных групп над конечными полями образуют большие развитые направления теории конечных групп, имеющих приложения в физике.

Также хорошо развита теория нильпотентных и разрешимых групп, содержащих все абелевы группы, а также многочисленных их обобщений: локально нильпотентных групп; локально разрешимых групп; групп с нормализаторным условием; групп с субнормальными системами подгрупп различного типа [6].

Современная теория представлений групп и теория характеров представляет сложившуюся область, обогащенную методами теории колец и гомологической алгебры с мощным арсеналом технических средств для исследования абстрактных групп.

В физике теория характеров применяется для изучения приводимых представлений, разложения его на неприводимые. Она значительно упрощает получение новых результатов.

Выводы

В данной статье был исследован в общих чертах «путь», который прошла теория групп и отмечен ряд её применений в современной науке.

Теория групп, порожденная впервые задачами теории алгебраических уравнений, превратилась в мощную и разветвленную область знаний. Она имеет три исторических корня: теорию алгебраических уравнений, теорию чисел и геометрию. Начиная с конца XIX века, она оказывала огромное влияние на развитие математического анализа, геометрии, механики и, наконец, физики. Она впоследствии проникла в другие области математики – появились группы Ли в теории дифференциальных уравнений, группы Клейна в геометрии. Возникли также группы Галилея в механике и группы Лоренца в теории относительности.

В настоящий момент теория групп является важной частью более глобальной области науки – общей алгебры. В теории групп в настоящий момент много перспективных направлений, которые активно развиваются учеными всего мира.

Список использованной литературы

1. Колмогоров А. Н., Юшкевичк А. П. Математика XIX века. Математическая логика. Алгебра. Теория чисел. Теория вероятностей / Колмогоров А. Н. - М., 1978, – 256 с.
2. Вейль Г. Теория групп и квантовая механика/ Вейль Г. - М.: Издательство Наука, 1986. – 496 с.
3. Хамермеш М. Теория групп и её применение к физическим проблемам/ Хамермеш М. – М.: Мир, 1966. – 587 с.
4. Вигнер Е. Теория групп и её приложения к квантомеханической теории атомных спектров/ Вигнер Е. - Москва, 1961. – 444 с.
5. Петрашень М. И., Трифонов Е. Д. Применение теории групп в квантовой механике/ Петрашень М. И. - Москва.: Издательство Наука, 1967. – 308 с.
6. Курош А. Г. Теория групп/ Курош А. Г. - Москва: Издательство Наука, 1967. – 648 с.
7. Ашбахер М. Конечные простые группы и их классификация. // УМН - 1981. – Т. 36, вып. 2 (218). – c. 141-172.
8. Шмитд О. Ю. Абстрактная теория групп/ Шмидт О. Ю. - 2-е изд. - М.; Л.: Гос. технико-теорет. изд-во, 1933. – 180 с.