Об уравнении Шредингера

В курсе физики высшей школы уравнению Шредингера и связанных с ним задачам отводится весьма значительное место. Тем не менее, в традиционном изложении, в отличие от строгих выводов основополагающих уравнений в других разделах физики, уравнение Шредингера постулируется, что не всегда адекватно воспринимается студентами. В данной статье обращается внимание преподавателя на логически более ясный вариационный вывод уравнения Шредингера из принципа наименьшего действия. Использование подобного подхода представляется весьма полезным, по крайней мере, для процесса преподавания на уровне факультатива. Такой метод позволяет, с одной стороны, провести строгий вывод уравнения Шредингера, с другой, — наглядно показывает, что уравнение Шредингера представляет собой предельный случай более сложного уравнения, решения которого описывают релятивистские свойства микрообъекта.

Пусть имеется микрочастица, описываемая непрерывной, конечной и однозначной функцией Ψ(r, t). По сравнению с классической физикой, где состояние частицы определялось заданием в каждый момент времени координат и импульсов, состояние квантовой частицы будем описывать, фактически сопоставляя ей поле Ψ(r, t). Как известно, |Ψ|² имеет смысл поля вероятности. В итоге по сравнению с классической частицей, имеющей три степени свободы, квантовый микрообъект, обладающий свойствами и частицы, и волны, будет иметь бесконечное число степеней свободы. Если положение классической частицы в наиболее общем случае определялось 4-вектором, то состояние квантовой частицы будем определять бесконечно мерным вектором Ψ(r, t) = Ψ(x) в гильбертовом пространстве.

В классической физике функция Лагранжа системы с N степенями свободы определялась суммой

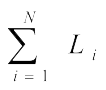
В нашем случае бесконечного числа степеней свободы функция Лагранжа определится интегралом по всему пространству:

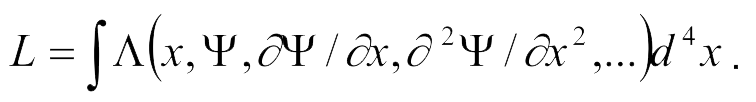
Λ(x,Ψ) назовем плотностью функции Лагранжа или лагранжианом. Тогда действие запишется в виде:

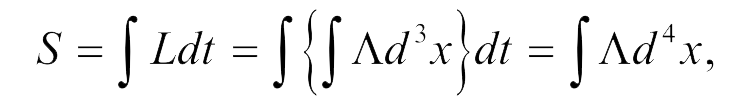
где d⁴x≡d³xcdt – элемент объема четырехмерного пространства, с – скорость света в вакууме.

Примем, что Λ = Λ(x,Ψ,δΨ/δx). Это необходимо сделать, чтобы при переходе к классической физике уравнения движения не содержали производных выше второго порядка (то есть чтобы движение полностью определялось заданием координат и скоростей [1]). Тогда, рассматривая действие как функционал, определенный на функциях Ψδ(x) (x) в четырехмерном пространстве, и требуя обращения в ноль вариаций Ψδ(x) (x) на границе области интегрирования, из принципа наименьшего действия после тривиальной математической процедуры получим уравнение Лагранжа-Эйлера:

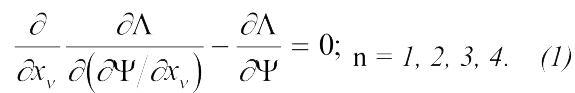
Вид лагранжиана для свободной частицы легко установить из соображения симметрии (напомним, что функция Лагранжа для свободной частицы в классической физике также определялась из соображения симметрии [1]). Если потребовать, чтобы уравнение движения квантовой частицы было линейно, инвариантно относительно трансляций и преобразований Лоренца, то с точностью до мультипликативного множителя и аддитивной четырехдивергенции (см. например, [2])

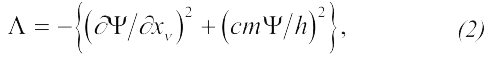
где множитель (-1) взят, чтобы энергия была положительна, а m – вещественный параметр, имеющий смысл массы покоя частицы.

Подставим (2) в (1) и получим уравнение движения квантовой частицы:

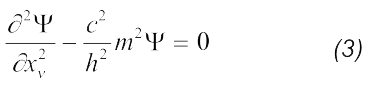
или

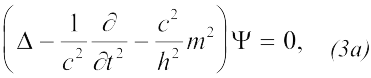
где Δ – оператор Лапласа. В данном месте вывода, не вдаваясь в обсуждение релятивистских особенностей, следует отметить, что уравнение (3) есть уравнение Клейна-Гордона, что его решение описывает состояние релятивистской квантовой частицы. При c → ∞ уравнение (3a) должно при водиться к уравнению для нерелятивистской квантовой частицы. Для перехода к нерелятивистскому пределу следует учесть, что энергия в релятивистском и нерелятивистском случаях отсчитывается от разных начальных значений. Примем: E_рел – E_рел = mc²

С учетом этого в (3a) примем

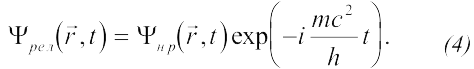
Подставим (4) в (3a) и при c → ∞ получим уравнение свободного движения нерелятивистской квантовой частицы, которое называется уравнением Шредингера:

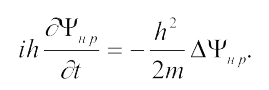
Предлагаемый вывод уравнения Шредингера, несмотря на схематичность и кажущуюся слож- ность, представляется более убедительным, чем стандартные для учебников утверждения, что уравнение Шредингера не выводится, а постулируется и что его справедливость подтверждается практикой. Повторять же на занятиях логику рассуждений Шредингера, приведших к получению уравнения, нет возможности ввиду ограниченности лекционного времени. Качественные рассуждения, «на пальцах», только еще более путают студентов. В этой связи предлагаемый вывод может быть полезен, и если его гносеологическая ценность невелика, то психологическое влияние несомненно положительно.

Кроме того, предлагаемый вывод уравнения Шредингера существенно упрощает подход к изучению релятивистских свойств микрочастиц, так как студенты сразу видят, что уравнение Шредингера есть просто нерелятивистский предел другого, более сложного уравнения, решения которого описывают релятивистские свойства микрообъекта.

Отметим также, что все законы сохранения квантовых частиц легко могут быть получены из (1), теоремы Неттерра (известной студентам по курсу теоретической механики и математической физики) и требования симметрии уравнений Лагранжа.

Список использованной литературы

1. Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1973. 208 с.
2. Боголюбов Н.Н., Ширков Д.В. Квантовые поля. М.: Наука, 1980. 320 с.